Continued Fractions

A continued fraction is an expression of the form

$$a_0 + \frac{1}{\displaystyle a_1+\frac{1}{\displaystyle a_2+\frac{1}{\displaystyle a_3+\cdots.}}}$$

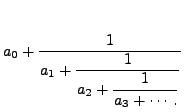
In this book we will assume that the $a_i$ are real numbers and $a_i>0$ for $i\geq 1$ , and the expression may or may not go on indefinitely. More general notions of continued fractions have been extensively studied, but they are beyond the scope of this book. We will be most interested in the case when the $a_i$ are all integers.

We denote the continued fraction displayed above by

$$[a_0,a_1,a_2,\ldots].$$

For example,

$$[1,2] = 1+\frac{1}{2} = \frac{3}{2},$$

$$[3, 7, 15, 1, 292 ] = 3 + \frac{1}{\displaystyle 7+ \frac{1}{\displaystyle 15+\frac{1}{\displaystyle 1+\frac{1}{292}}}}$$

$$= \frac{103993}{33102}=3.14159265301190260407\ldots,$$

and

$$[2, 1, 2, 1, 1, 4, 1, 1, 6] = 2 + \frac{1}{\displaystyle 1 +\frac{1}{\displaystyle 2 +\frac{1... ...}{\displaystyle 1 + \frac{1}{\displaystyle 1 + \frac{1}{\displaystyle 6}}}}}}}}$$

$$= \frac{1264}{465}$$

$$= 2.7182795698924731182795698\ldots$$

The second two examples were chosen to foreshadow that continued fractions can be used to obtain good rational approximations to irrational numbers. Note that the first approximates $\pi$ and the second $e$ .

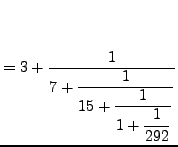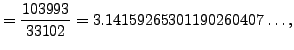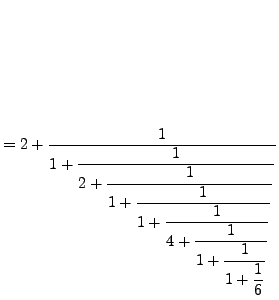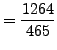Continued fractions have many applications. For example, they provide an algorithmic way to recognize a decimal approximation to a rational number. Continued fractions also suggest a sense in which $e$ might be ``less complicated'' than $\pi$ (see Example 5.2.4 and Section 5.3).

In Section 5.1 we study continued fractions $[a_0,a_1,\ldots,a_n]$ of finite length and lay the foundations for our later investigations. In Section 5.2 we give the continued fraction procedure, which associates to a real number $x$ a sequence $a_0,a_1,\ldots$ of integers such that $x = \lim_{n\rightarrow \infty} [a_0,a_1,\ldots,a_n]$ . We also prove that if $a_0,a_1,\ldots$ is any infinite sequence of positive integers, then the sequence $c_n=[a_0,a_1,\ldots,a_n]$ converges; more generally, we prove that if the $a_n$ are arbitrary positive real numbers and $\sum_{n=0}^{\infty} a_n$ diverges then $(c_n)$ converges. In Section 5.4, we prove that a continued fraction with $a_i\in\mathbb{N}$ is (eventually) periodic if and only if its value is a non-rational root of a quadratic polynomial, then discuss open questions concerning continued fractions of roots of irreducible polynomials of degree greater than $2$ . We conclude the chapter with applications of continued fractions to recognizing approximations to rational numbers (Section 5.5) and writing integers as sums of two squares (Section 5.6).

The reader is encouraged to read more about continued fractions in [#!hardywright!#, Ch. X], [#!khintchine!#], [#!burton!#, §13.3], and [#!niven-zuckerman-montgomery!#, Ch. 7].