Next: Convergence of Infinite Continued Up: Infinite Continued Fractions Previous: Infinite Continued Fractions Contents Index
with
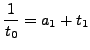
with
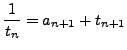
with
![$\displaystyle \frac{8}{3} = [2,1,2],$](img1700.png)
so the continued fraction procedure produces the continued fraction of
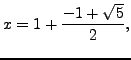
so
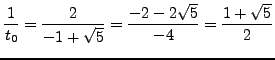
so again
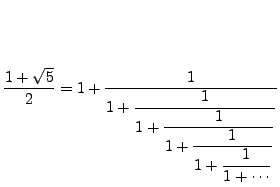
sage: def cf(bits): ... x = (1 + sqrt(RealField(bits)(5))) / 2 ... return continued_fraction(x) sage: cf(10) [1, 1, 1, 1, 1, 1, 1, 3] sage: cf(30) [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2] sage: cf(50) [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
For example,
The ![]() th partial convergent of the continued fraction of
th partial convergent of the continued fraction of ![]() is
is
![$\displaystyle [a_0,a_1,a_2,a_3,a_4,a_5] = \frac{87}{32} = 2.71875,
$](img1714.png)
which is a good rational approximation to
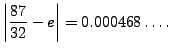
Note that
Let's do the same thing with
![]() :
Applying the continued fraction procedure, we find that
the continued fraction of
:
Applying the continued fraction procedure, we find that
the continued fraction of ![]() is
is
The first few partial convergents are
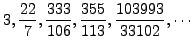
These are good rational approximations to
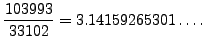
Notice that the continued fraction of ![]() exhibits a nice pattern (see
Section 5.3 for a proof), whereas the continued
fraction of
exhibits a nice pattern (see
Section 5.3 for a proof), whereas the continued
fraction of ![]() exhibits no pattern that is obvious to the author.
The continued fraction of
exhibits no pattern that is obvious to the author.
The continued fraction of ![]() has been extensively studied, and over
20 million terms have been computed. The data suggests that every
integers appears infinitely often as a partial convergent. For much
more about the continued fraction of
has been extensively studied, and over
20 million terms have been computed. The data suggests that every
integers appears infinitely often as a partial convergent. For much
more about the continued fraction of ![]() or of any other sequence
in this book, type the first few terms of the sequence
into [#!sloane!#].
or of any other sequence
in this book, type the first few terms of the sequence
into [#!sloane!#].
William 2007-06-01