Infinite Continued Fractions
This section begins with the continued fraction procedure, which associates
to a real number 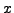 a sequence
a sequence
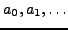 of integers. After
giving several examples, we prove that
of integers. After
giving several examples, we prove that
![$ x = \lim_{n\rightarrow \infty}
[a_0,a_1,\ldots,a_n]$](img1563.png) by proving that the odd and even partial
convergents become arbitrarily close to each other.
We also show that if
by proving that the odd and even partial
convergents become arbitrarily close to each other.
We also show that if
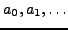 is any infinite
sequence of positive integers, then the sequence of
is any infinite
sequence of positive integers, then the sequence of
![$ c_n=[a_0,a_1,\ldots,a_n]$](img1564.png) converges, and, more generally, if
converges, and, more generally, if 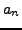 is an arbitrary sequence
of positive reals
such that
is an arbitrary sequence
of positive reals
such that
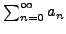 diverges then
diverges then 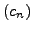 converges.
converges.
Subsections
William
2007-06-01