Partial Convergents

Fix a finite continued fraction $[a_0,\ldots,a_m]$ . We do not assume at this point that the $a_i$ are integers.

Definition 5.1 (Partial convergents)   For $0\leq n\leq m$ , the $n$ th convergent of the continued fraction $[a_0,\ldots,a_m]$ is $[a_0,\ldots, a_n]$ . These convergents for $n<m$ are also called partial convergents.

For each $n$ with $-2\leq n\leq m$ , define real numbers $p_n$ and $q_n$ as follows:

$$\begin{array}{lllcl} p_{-2}=0, & \quad p_{-1} = 1, & \quad p... ...dots & q_n = a_n q_{n-1} + q_{n-2} \quad \cdots. \end{array}$$

Proposition 5.1 (Partial Convergents)   For $n\geq 0$ with $n\leq m$ we have

$$[a_0, \ldots, a_n] = \frac{p_n}{q_n}.$$

Proof. We use induction. The assertion is obvious when $n=0,1$ . Suppose the proposition is true for all continued fractions of length $n-1$ . Then

$$[a_0,\ldots, a_n] = [a_0,\ldots,a_{n-2}, a_{n-1} + \frac{1}{a_n}]$$

$$= \frac{\left( a_{n-1} + \frac{1}{a_n}\right) p_{n-2} + p_{n-3}} {\left( a_{n-1} + \frac{1}{a_n}\right) q_{n-2} + q_{n-3}}$$

$$= \frac{(a_{n-1}a_n +1)p_{n-2} + a_n p_{n-3}} {(a_{n-1}a_n +1)q_{n-2} + a_n q_{n-3}}$$

$$= \frac{a_n(a_{n-1}p_{n-2} + p_{n-3}) + p_{n-2}} {a_n(a_{n-1}q_{n-2} + q_{n-3}) + q_{n-2}}$$

$$= \frac{a_n p_{n-1} + p_{n-2}}{a_n q_{n-1} + q_{n-2}}$$

$$= \frac{p_n}{q_n}.$$

$\qedsymbol$

SAGE Example 5.1   If c is a continued fraction in SAGE, use c.convergents() to compute a list of the partial convergents of c.

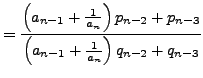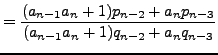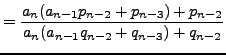sage: c = continued_fraction(pi,bits=33); c
[3, 7, 15, 1, 292, 2]
sage: c.convergents() 
[3, 22/7, 333/106, 355/113, 103993/33102, 208341/66317]

As we will see, the convergents of a continued fraction are the best rational approximations to the value of the continued fraction. In the example above, the listed convergents are the best rational approximations of $\pi$ with given denominator size.

Proposition 5.1   For $n\geq 0$ with $n\leq m$ we have

$$p_n q_{n-1} - q_n p_{n-1} = (-1)^{n-1}$$ (5.1.2)

and

$$p_nq_{n-2} - q_n p_{n-2} = (-1)^n a_n.$$ (5.1.3)

Equivalently,

$$\frac{p_n}{q_n} - \frac{p_{n-1}}{q_{n-1}} = (-1)^{n-1}\cdot\frac{1}{q_n q_{n-1}}$$

and

$$\frac{p_n}{q_n} - \frac{p_{n-2}}{q_{n-2}} = (-1)^{n}\cdot\frac{a_n}{q_n q_{n-2}}.$$

Proof. The case for $n=0$ is obvious from the definitions. Now suppose $n>0$ and the statement is true for $n-1$ . Then

$$p_{n}q_{n-1} - q_n p_{n-1} = (a_n p_{n-1} + p_{n-2}) q_{n-1} - (a_n q_{n-1} + q_{n-2}) p_{n-1}$$

$$= p_{n-2}q_{n-1} - q_{n-2} p_{n-1}$$

$$= -(p_{n-1}q_{n-2} - p_{n-2} q_{n-1})$$

$$= -(-1)^{n-2} = (-1)^{n-1}.$$

This completes the proof of (5.1.2). For (5.1.3), we have

$$p_n q_{n-2} - p_{n-2} q_n = (a_n p_{n-1} + p_{n-2})q_{n-2} - p_{n-2}(a_n q_{n-1} + q_{n-2})$$

$$= a_n(p_{n-1}q_{n-2} - p_{n-2}q_{n-1})$$

$$= (-1)^n a_n.$$

$\qedsymbol$

Remark 5.1   Expressed in terms of matrices, the proposition asserts that the determinant of $\left(\begin{smallmatrix}p_n&p_{n-1} q_n&q_{n-1}\end{smallmatrix}\right)$ is $(-1)^{n-1}$ , and of $\left(\begin{smallmatrix}p_n&p_{n-2} q_n&q_{n-2}\end{smallmatrix}\right)$ is $(-1)^{n}a_n$ .

SAGE Example 5.1   We use SAGE to verify Proposition 5.1.7 for the first few terms of the continued fraction of $\pi$ .

sage: c = continued_fraction(pi); c 
[3, 7, 15, 1, 292, 1, 1, 1, 2, 1, 3, 1, 14, 3]
sage: for n in range(-1, len(c)):
...    print c.pn(n)*c.qn(n-1) - c.qn(n)*c.pn(n-1),
1 -1 1 -1 1 -1 1 -1 1 -1 1 -1 1 -1 1 
sage: for n in range(len(c)):
...    print c.pn(n)*c.qn(n-2) - c.qn(n)*c.pn(n-2), 
3 -7 15 -1 292 -1 1 -1 2 -1 3 -1 14 -3

Corollary 5.1 (Convergents in lowest terms)   If $[a_0,a_1,\ldots, a_m]$ is a simple continued fraction, so each $a_i$ is an integer, then the $p_n$ and $q_n$ are integers and the fraction $p_n/q_n$ is in lowest terms.

Proof. It is clear that the $p_n$ and $q_n$ are integers, from the formula that defines them. If $d$ is a positive divisor of both $p_n$ and $q_n$ , then $d\mid (-1)^{n-1}$ , so $d=1$ . $\qedsymbol$

SAGE Example 5.1   We illustrate Corollary 5.1.10 using SAGE.

sage: c = continued_fraction([1,2,3,4,5]) 
sage: c.convergents() 
[1, 3/2, 10/7, 43/30, 225/157]
sage: [c.pn(n) for n in range(len(c))] 
[1, 3, 10, 43, 225]
sage: [c.qn(n) for n in range(len(c))]  
[1, 2, 7, 30, 157]