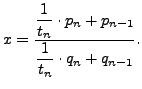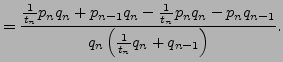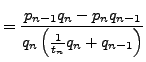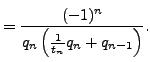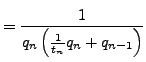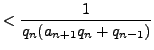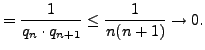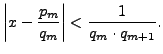Proof.
We use induction. The statements are both true when
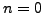
.
If the second statement is true for
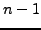
, then
Similarly, the first statement is true for
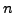
if
it is true for
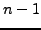
.

Proof.
For any
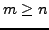
, the number
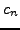
is a partial convergent of
![$ [a_0,\ldots,a_m]$](img1591.png)
. By Proposition
5.1.13 the
even convergents
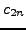
form a strictly
increasing sequence
and the odd convergents
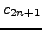
form a strictly
decreasing
sequence. Moreover, the even convergents are all
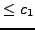
and the
odd convergents are all
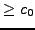
. Hence
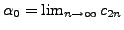
and
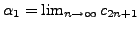
both
exist and
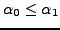
. Finally, by
Proposition
5.1.7
so
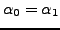
.

We define
Example 5.2
We illustrate the theorem with
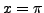
.
As in the proof of Theorem
5.2.6,
let
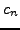
be the
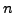
th partial convergent
to
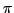
. The
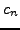
with
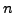
odd converge down to
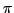
whereas the
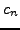
with
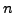
even converge up to
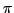
Theorem 5.2
Let
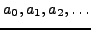 be a sequence of real numbers
such that
be a sequence of real numbers
such that 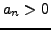 for all
for all 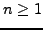 , and for each
, and for each 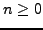 , set
, set
![$ c_n = [a_0, a_1, \ldots a_n].$](img1727.png) Then
Then
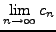 exists if and only if the sum
exists if and only if the sum
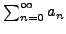 diverges.
diverges.
Proof.
We only prove that if
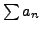
diverges then
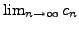
exists. A proof of the converse can be found in
[#!wall!#, Ch. 2, Thm. 6.1].
Let 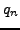 be the sequence of ``denominators''
of the partial convergents, as defined in Section 5.1.1,
so
be the sequence of ``denominators''
of the partial convergents, as defined in Section 5.1.1,
so 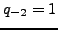 ,
, 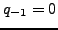 , and for
, and for 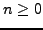 ,
,
As we saw in the proof of Theorem
5.2.6,
the limit
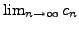
exists provided that
the sequence
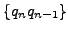
diverges to positive infinity.
For 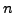 even,
even,
and for
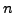
odd,
Since
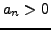
for
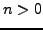
, the sequence
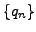
is increasing, so
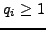
for all
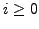
.
Applying this fact to the above expressions for
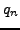
, we see that
for
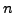
even
and for
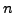
odd
If 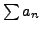 diverges, then at least one of
diverges, then at least one of
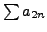 or
or
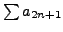 must diverge. The
above inequalities then imply that
at least one of the sequences
must diverge. The
above inequalities then imply that
at least one of the sequences
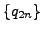 or
or
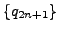 diverge to infinity.
Since
diverge to infinity.
Since 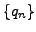 is an increasing sequence, it follows
that
is an increasing sequence, it follows
that
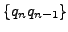 diverges to infinity.
diverges to infinity.

Example 5.2
Let
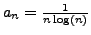
for
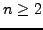
and
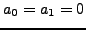
. By the
integral test,
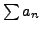
diverges, so by Theorem
5.2.8
the continued fraction
![$ [a_0,a_1,a_2,\ldots]$](img1766.png)
converges.
This convergence is very slow, since, e.g.
yet
Theorem 5.2
Let
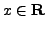 be a real number. Then
be a real number. Then 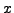 is the value
of the (possibly infinite) simple continued fraction
is the value
of the (possibly infinite) simple continued fraction
![$ [a_0,a_1,a_2,\ldots]$](img1766.png) produced by the continued fraction procedure.
produced by the continued fraction procedure.
Proof.
If the sequence is finite then some
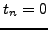
and the
result follows by Lemma
5.2.5.
Suppose the sequence is infinite.
By Lemma
5.2.5,
By Proposition
5.1.5 (which we apply in a case when
the partial quotients of the continued fraction are not integers!),
we have
Thus if
![$ c_n=[a_0,a_1,\ldots,a_n]$](img1564.png)
, then
Thus
In the inequality we use that
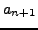
is the integer part of
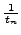
, and is hence
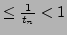
, since
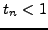
.

This corollary follows from the proof of the above theorem.
Corollary 5.2 (Convergence of continued fraction)
Let
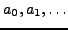 define a simple continued
fraction, and let
define a simple continued
fraction, and let
![$ x=[a_0,a_1,\ldots]\in\mathbb{R}$](img1784.png) be its value.
Then for all
be its value.
Then for all 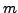 ,
,
Proposition 5.2
If 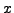 is a rational number then the sequence
is a rational number then the sequence
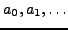 produced by the continued fraction procedure terminates.
produced by the continued fraction procedure terminates.
Proof.
Let
![$ [b_0,b_1,\ldots, b_m]$](img1786.png)
be the continued fraction representation
of
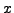
that we obtain using Algorithm
1.1.13, so the
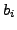
are the partial quotients at each step.
If
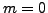
, then
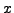
is an integer, so we may assume
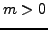
.
Then
If
![$ [b_1,\ldots,b_m]=1$](img1789.png)
then
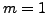
and
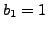
,
which will not happen using Algorithm
1.1.13, since
it would give
![$ [b_0+1]$](img1792.png)
for the continued fraction of
the integer
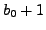
.
Thus
![$ [b_1,\ldots,b_m]>1$](img1794.png)
, so in the continued fraction
algorithm we choose
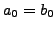
and
![$ t_0 = 1/[b_1, \ldots, b_m]$](img1796.png)
.
Repeating this argument enough times proves the claim.

William
2007-06-01
![$\displaystyle = \left[a_0,a_1, \ldots, a_{n-1},\frac{1}{t_{n-1}}\right]$](img1724.png)
![$\displaystyle =\left[a_0,a_1, \ldots, a_{n-1},a_n, \frac{1}{t_n}\right].$](img1726.png)
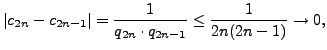
![]() be the sequence of ``denominators''
of the partial convergents, as defined in Section 5.1.1,
so
be the sequence of ``denominators''
of the partial convergents, as defined in Section 5.1.1,
so ![]() ,
, ![]() , and for
, and for ![]() ,
,
![]() even,
even,
![]() diverges, then at least one of
diverges, then at least one of
![]() or
or
![]() must diverge. The
above inequalities then imply that
at least one of the sequences
must diverge. The
above inequalities then imply that
at least one of the sequences
![]() or
or
![]() diverge to infinity.
Since
diverge to infinity.
Since ![]() is an increasing sequence, it follows
that
is an increasing sequence, it follows
that
![]() diverges to infinity.
diverges to infinity.
![]()
![$\displaystyle x = [a_0, a_1, \ldots, a_n, \frac{1}{t_n}].
$](img1770.png)