The Sequence of Partial Convergents

Let $[a_0,\ldots,a_m]$ be a continued fraction and for $n\leq m$ let

$$c_n = [a_0, \ldots, a_n] = \frac{p_n}{q_n}$$

denote the $n$ th convergent. Recall that by definition of continued fraction, $a_n>0$ for $n>0$ , which gives the partial convergents of a continued fraction additional structure. For example, the partial convergents of $[2, 1, 2, 1, 1, 4, 1, 1, 6]$ are

$$2, 3, 8/3, 11/4, 19/7, 87/32, 106/39, 193/71, 1264/465.$$

To make the size of these numbers clearer, we approximate them using decimals. We also underline every other number, to illustrate some extra structure.

$$\underline{2}, 3, \underline{2.66667}, 2.75000, \underline{2.71429}, 2.71875, \underline{2.71795}, 2.71831, \underline{2.71828}$$

The underlined numbers are smaller than all of the non-underlined numbers, and the sequence of underlined numbers is strictly increasing, whereas the non-underlined numbers strictly decrease.

SAGE Example 5.1   We graphically illustrate the above pattern on another continued fraction using SAGE.

sage: c = continued_fraction([1,1,1,1,1,1,1,1])
sage: v = [(i, c.pn(i)/c.qn(i)) for i in range(len(c))]
sage: P = point(v, rgbcolor=(0,0,1), pointsize=40)
sage: L = line(v, rgbcolor=(0.5,0.5,0.5)) 
sage: L2 = line([(0,c.value()),(len(c)-1,c.value())], \
...      thickness=0.5, rgbcolor=(0.7,0,0)) 
sage.:(L+L2+P).show(ymin=1)

We next prove that this extra structure is a general phenomenon.

Proposition 5.1 (How convergents converge)   The even indexed convergents $c_{2n}$ increase strictly with $n$ , and the odd indexed convergents $c_{2n+1}$ decrease strictly with $n$ . Also, the odd indexed convergents $c_{2n+1}$ are greater than all of the even indexed convergents $c_{2m}$ .

Proof. The $a_n$ are positive for $n\geq 1$ , so the $q_n$ are positive. By Proposition 5.1.7, for $n\geq 2$ ,

$$c_n - c_{n-2} = (-1)^n \cdot \frac{a_n}{q_n q_{n-2} },$$

which proves the first claim.

Suppose for the sake of contradiction that there exist integers $r, m$ such that $c_{2m+1} < c_{2r}$ . Proposition 5.1.7 implies that for $n\geq 1$ ,

$$c_n - c_{n-1} = (-1)^{n-1}\cdot \frac{1}{q_n q_{n-1}}$$

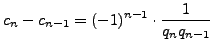
has sign $(-1)^{n-1}$ , so for all $s\geq 0$ we have $c_{2s+1} > c_{2s}$ . Thus it is impossible that $r= m$ . If $r<m$ , then by what we proved in the first paragraph, $c_{2m+1} < c_{2r} < c_{2m}$ , a contradiction (with $s=m$ ). If $r>m$ , then $c_{2r+1} < c_{2m+1} < c_{2r}$ , which is also a contradiction (with $s=r$ ). $\qedsymbol$