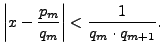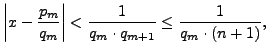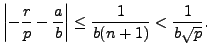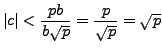Sums of Two Squares
In this section we apply continued fractions to prove
the following theorem.
Theorem 5.6
A positive integer  is a sum of two squares if and only if all
prime factors of
is a sum of two squares if and only if all
prime factors of 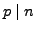 such that
such that
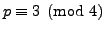 have even
exponent in the prime factorization of
have even
exponent in the prime factorization of  .
.
We first consider some examples. Notice that
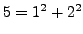 is a sum
of two squares, but
is a sum
of two squares, but 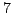 is not a sum of two squares. Since
is not a sum of two squares. Since 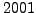 is
divisible by
is
divisible by 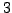 (because
(because 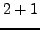 is divisible by
is divisible by 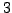 ),
but not by
),
but not by 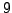 (since
(since 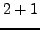 is not),
Theorem 5.6.1 implies that
is not),
Theorem 5.6.1 implies that 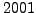 is not a sum of two
squares. The theorem also implies that
is not a sum of two
squares. The theorem also implies that
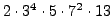 is a sum of two squares.
is a sum of two squares.
SAGE Example 5.6
We use SAGE to write a short program that
naively determines
whether or not an integer

is a sum of two squares, and if
so returns
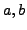
such that
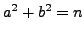
.
sage: def sum_of_two_squares_naive(n):
... for i in range(int(sqrt(n))):
... if is_square(n - i^2):
... return i, (Integer(n-i^2)).sqrt()
... return "%s is not a sum of two squares"%n
We next use our function in a couple of cases.
sage: sum_of_two_squares_naive(23)
'23 is not a sum of two squares'
sage: sum_of_two_squares_naive(389)
(10, 17)
sage: sum_of_two_squares_naive(2007)
'2007 is not a sum of two squares'
sage: sum_of_two_squares_naive(2008)
'2008 is not a sum of two squares'
sage: sum_of_two_squares_naive(2009)
(28, 35)
sage: 28^2 + 35^2
2009
sage: sum_of_two_squares_naive(2*3^4*5*7^2*13)
(189, 693)
Definition 5.6 (Primitive)
A representation
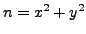
is
primitive
if
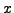
and
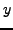
are coprime.
Lemma 5.6
If  is divisible by a prime
is divisible by a prime
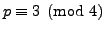 , then
, then  has no primitive representations.
has no primitive representations.
Proof.
Suppose

has a primitive representation,
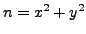
, and
let

be any prime factor of

. Then
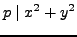
and
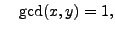
so
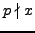
and
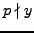
.
Since
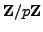
is a field we may divide by
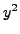
in the equation
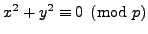
to see that
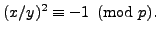
Thus the Legendre symbol
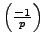
equals
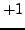
.
However, by Proposition
4.2.1,
so
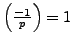
if and only if
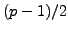
is even, which is
to say
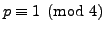
.

Proof.
[Proof of Theorem
5.6.1
]
Suppose that
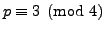
is a prime, that
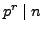
but
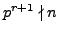
with
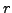
odd, and that
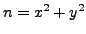
. Letting
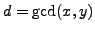
, we have
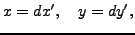
and
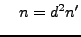
with
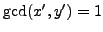
and
Because
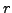
is odd,
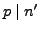
, so Lemma
5.6.4
implies that
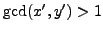
, a contradiction.

To prepare for our proof of
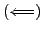 , we reduce
the problem to the case when
, we reduce
the problem to the case when  is prime. Write
is prime. Write
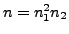 where
where
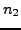 has no prime factors
has no prime factors
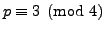 . It suffices to show
that
. It suffices to show
that 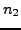 is a sum of two squares, since
is a sum of two squares, since
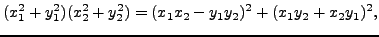 |
(5.6.1) |
so a product of two numbers that are sums of two squares is also
a sum of two squares.
Since 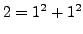 is a sum of two squares, it suffices to show
that any prime
is a sum of two squares, it suffices to show
that any prime
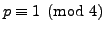 is a sum of two squares.
is a sum of two squares.
Proof.
Consider the continued fraction
![$ [a_0, a_1, \ldots]$](img1897.png)
of
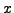
.
By Corollary
5.2.11, for each
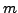
Since
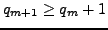
and
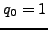
,
either there exists an
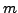
such that
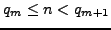
, or the
continued fraction
expansion of
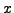
is finite and

is larger
than the denominator of the rational number
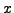
, in which case
we take
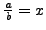
and are done. In the first
case,
so
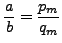
satisfies the conclusion of
the lemma.

Proof.
[Proof of Theorem
5.6.1
]
As discussed above, it suffices to prove that any prime
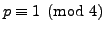
is a sum of two squares. Since
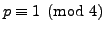
,
so Proposition
4.2.1 implies that
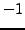
is a square modulo

; i.e., there exists
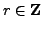
such
that
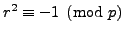
.
Lemma
5.6.5, with
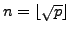
and
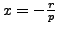
,
implies that there are integers
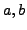
such that
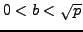
and
Letting
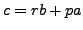
, we have that
so
But
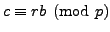
, so
Thus
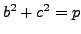
.

Remark 5.6
Our proof of Theorem
5.6.1 leads to an efficient
algorithm to compute a representation of any
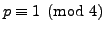
as a sum of two squares.
SAGE Example 5.6
We next use SAGE and Theorem
5.6.1 to
give an efficient algorithm for writing a prime
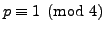
as a sum of two squares. First we implement the algorithm
that comes out of the proof of the theorem.
sage: def sum_of_two_squares(p):
... p = Integer(p)
... assert p%4 == 1, "p must be 1 modulo 4"
... r = Mod(-1,p).sqrt().lift()
... v = continued_fraction(-r/p)
... n = floor(sqrt(p))
... for x in v.convergents():
... c = r*x.denominator() + p*x.numerator()
... if -n <= c and c <= n:
... return (abs(x.denominator()),abs(c))
Next we use the algorithm to write the first
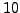
-digit
prime
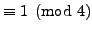
as a sum of two squares:
sage: p = next_prime(next_prime(10^10))
sage: sum_of_two_squares(p)
(55913, 82908)
The above calculation was essentially instantanoues.
If instead we use the naive algorithm from before,
it takes several seconds to write

as a sum of two squares.
sage: sum_of_two_squares_naive(p)
(55913, 82908)
William
2007-06-01
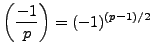
![]() , we reduce
the problem to the case when
, we reduce
the problem to the case when ![]() is prime. Write
is prime. Write
![]() where
where
![]() has no prime factors
has no prime factors
![]() . It suffices to show
that
. It suffices to show
that ![]() is a sum of two squares, since
is a sum of two squares, since