Preface¶
This is a graduate-level textbook about algorithms for computing with modular forms. It is nontraditional in that the primary focus is not on underlying theory; instead, it answers the question how do you use a computer to explicitly compute spaces of modular forms?
This book emerged from notes for a course the author taught at Harvard University in 2004, a course at UC San Diego in 2005, and a course at the University of Washington in 2006.
The author has spent years trying to find good practical ways to
compute with classical modular forms for congruence subgroups of
 and has implemented most of these algorithms several
times, first in C++ [Ste99b], then in MAGMA [BCP97],
and as part of the free open source computer algebra system Sage
(see [Ste06]). Much of this work has involved turning formulas
and constructions buried in obscure research papers into precise
computational recipes then testing these and eliminating inaccuracies.
and has implemented most of these algorithms several
times, first in C++ [Ste99b], then in MAGMA [BCP97],
and as part of the free open source computer algebra system Sage
(see [Ste06]). Much of this work has involved turning formulas
and constructions buried in obscure research papers into precise
computational recipes then testing these and eliminating inaccuracies.
The author is aware of no other textbooks on computing with modular forms, the closest work being Cremona’s book [Cre97a], which is about computing with elliptic curves, and Cohen’s book [Coh93] about algebraic number theory.
In this book we focus on how to compute in practice the spaces
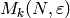 of modular forms, where
of modular forms, where 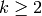 is an integer and
is an integer and
 is a Dirichlet character of modulus
is a Dirichlet character of modulus  (the appendix treats
modular forms for higher rank groups). We spend the most effort
explaining the general algorithms that appear so far to be the best
(in practice!) for such computations. We will not discuss in any
detail computing with quaternion algebras, half-integral weight forms,
weight 1 forms, forms for noncongruence subgroups or groups other than
(the appendix treats
modular forms for higher rank groups). We spend the most effort
explaining the general algorithms that appear so far to be the best
(in practice!) for such computations. We will not discuss in any
detail computing with quaternion algebras, half-integral weight forms,
weight 1 forms, forms for noncongruence subgroups or groups other than
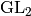 , Hilbert and Siegel modular forms, trace formulas,
, Hilbert and Siegel modular forms, trace formulas,  -adic
modular forms, and modular abelian varieties, all of which are topics
for additional books. We also rarely analyze the complexity of the
algorithms, but instead settle for occasional remarks about their
practical efficiency.
-adic
modular forms, and modular abelian varieties, all of which are topics
for additional books. We also rarely analyze the complexity of the
algorithms, but instead settle for occasional remarks about their
practical efficiency.
For most of this book we assume the reader has some prior exposure to modular forms (e.g., [DS05]), though we recall many of the basic definitions. We cite standard books for proofs of the fundamental results about modular forms that we will use. The reader should also be familiar with basic algebraic number theory, linear algebra, complex analysis (at the level of [Ahl78]), and algorithms (e.g., know what an algorithm is and what big oh notation means). In some of the examples and applications we assume that the reader knows about elliptic curves at the level of [Sil82].
Chapter Modular Forms is foundational for the rest of this book. It
introduces congruence subgroups of  and modular forms as
functions on the complex upper half plane. We discuss
and modular forms as
functions on the complex upper half plane. We discuss  -expansions,
which provide an important computational handle on modular forms. We
also study an algorithm for computing with congruence subgroups. The
chapter ends with a list of applications of modular forms throughout
mathematics.
-expansions,
which provide an important computational handle on modular forms. We
also study an algorithm for computing with congruence subgroups. The
chapter ends with a list of applications of modular forms throughout
mathematics.
In Chapter Modular Forms of Level 1 we discuss level 1 modular forms in much
more detail. In particular, we introduce Eisenstein series and the
cusp form  and describe their
and describe their  -expansions and basic
properties. Then we prove a structure theorem for level 1 modular
forms and use it to deduce dimension formulas and give an algorithm
for explicitly computing a basis. We next introduce Hecke operators
on level 1 modular forms, prove several results about them, and deduce
multiplicativity of the Ramanujan
-expansions and basic
properties. Then we prove a structure theorem for level 1 modular
forms and use it to deduce dimension formulas and give an algorithm
for explicitly computing a basis. We next introduce Hecke operators
on level 1 modular forms, prove several results about them, and deduce
multiplicativity of the Ramanujan 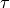 function as an application.
We also discuss explicit computation of Hecke operators. In Section
Fast Computation of Fourier Coefficients we make some brief remarks on recent work on
asymptotically fast computation of values of
function as an application.
We also discuss explicit computation of Hecke operators. In Section
Fast Computation of Fourier Coefficients we make some brief remarks on recent work on
asymptotically fast computation of values of 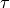 . Finally, we
describe computation of constant terms of Eisenstein series using an
analytic algorithm. We generalize many of the constructions in this
chapter to higher level in subsequent chapters.
. Finally, we
describe computation of constant terms of Eisenstein series using an
analytic algorithm. We generalize many of the constructions in this
chapter to higher level in subsequent chapters.
In Chapter Modular Forms of Weight 2 we turn to modular forms of higher level
but restrict for simplicity to weight  since much is clearer in
this case. (We remove the weight restriction later in Chapter
General Modular Symbols.) We describe a geometric way of viewing cuspidal
modular forms as differentials on modular curves, which leads to
modular symbols, which are an explicit way to present a certain
homology group. This chapter closes with methods for explicitly
computing cusp forms of weight 2 using modular symbols, which we
generalize in Chapter Computing with Newforms.
since much is clearer in
this case. (We remove the weight restriction later in Chapter
General Modular Symbols.) We describe a geometric way of viewing cuspidal
modular forms as differentials on modular curves, which leads to
modular symbols, which are an explicit way to present a certain
homology group. This chapter closes with methods for explicitly
computing cusp forms of weight 2 using modular symbols, which we
generalize in Chapter Computing with Newforms.
In Chapter Dirichlet Characters we introduce Dirichlet characters, which are important both in explicit construction of Eisenstein series (in Chapter Eisenstein Series and Bernoulli Numbers) and in decomposing spaces of modular forms as direct sums of simpler spaces. The main focus of this chapter is a detailed study of how to explicitly represent and compute with Dirichlet characters.
Chapter Eisenstein Series and Bernoulli Numbers is about how to explicitly construct the Eisenstein subspace of modular forms. First we define generalized Bernoulli numbers attached to a Dirichlet character and an integer then explain a new analytic algorithm for computing them (which generalizes the algorithm in Chapter Modular Forms of Level 1). Finally we give without proof an explicit description of a basis of Eisenstein series, explain how to compute it, and give some examples.
Chapter Dimension Formulas records a wide range of dimension formulas for spaces of modular forms, along with a few remarks about where they come from and how to compute them.
Chapter Linear Algebra is about linear algebra over exact fields, mainly the rational numbers. This chapter can be read independently of the others and does not require any background in modular forms. Nonetheless, this chapter occupies a central position in this book, because the algorithms in this chapter are of crucial importance to any actual implementation of algorithms for computing with modular forms.
Chapter General Modular Symbols is the most important chapter in this book; it generalizes Chapter Modular Forms of Weight 2 to higher weight and general level. The modular symbols formulation described here is central to general algorithms for computing with modular forms.
Chapter Computing with Newforms applies the algorithms from Chapter General Modular Symbols to the problem of computing with modular forms. First we discuss decomposing spaces of modular forms using Dirichlet characters, and then explain how to compute a basis of Hecke eigenforms for each subspace using several approaches. We also discuss congruences between modular forms and bounds needed to provably generate the Hecke algebra.
Chapter Computing Periods is about computing analytic invariants
of modular forms. It discusses tricks for speeding convergence
of certain infinite series and sketches how to compute every
elliptic curve over  with given conductor.
with given conductor.
Chapter Solutions to Selected Exercises contains detailed solutions to most of the exercises in this book. (Many of these were written by students in a course taught at the University of Washington.)
Appendix Computing in Higher Rank deals with computational techniques
for working with generalizations of modular forms to more general
groups than  , such as
, such as 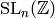 for
for 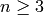 . Some of
this material requires more prerequisites than the rest of the book.
Nonetheless, seeing a natural generalization of the material in the
rest of this book helps to clarify the key ideas. The
topics in the appendix are directly related to the main themes of
this book: modular symbols, Manin symbols, cohomology
of subgroups of
. Some of
this material requires more prerequisites than the rest of the book.
Nonetheless, seeing a natural generalization of the material in the
rest of this book helps to clarify the key ideas. The
topics in the appendix are directly related to the main themes of
this book: modular symbols, Manin symbols, cohomology
of subgroups of  with various coefficients, explicit
computation of modular forms, etc.
with various coefficients, explicit
computation of modular forms, etc.
Software¶
We use Sage, Software for Algebra and Geometry Experimentation (see [Ste06]), to illustrate how to do many of the examples. Sage is completely free and packages together a wide range of open source mathematics software for doing much more than just computing with modular forms. Sage can be downloaded and run on your computer or can be used via a web browser over the Internet. The reader is encouraged to experiment with many of the objects in this book using Sage. We do not describe the basics of using Sage in this book; the reader should read the Sage tutorial (and other documentation) available at the Sage website [Ste06]. All examples in this book have been automatically tested and should work exactly as indicated in Sage version at least 1.5.
Acknowledgements¶
David Joyner and Gabor Wiese carefully read the book and provided a huge number of helpful comments.
John Cremona and Kevin Buzzard both made many helpful remarks that were important in the development of the algorithms in this book. Much of the mathematics (and some of the writing) in Chapter Computing Periods is joint work with Helena Verrill.
Noam Elkies made remarks about Chapters Modular Forms and Modular Forms of Level 1. Sándor Kovács provided interesting comments on Chapter Modular Forms. Allan Steel provided helpful feedback on Chapter Linear Algebra. Jordi Quer made useful remarks about Chapter Dirichlet Characters and Chapter Dimension Formulas.
The students in the courses that I taught on this material at Harvard, San Diego, and Washington provided substantial feedback: in particular, Abhinav Kumar made numerous observations about computing widths of cusps (see Section Computing Widths of Cusps) and Thomas James Barnet-Lamb made helpful remarks about how to represent Dirichlet characters. James Merryfield made helpful remarks about complex analytic issues and about convergence in Stirling’s formula. Robert Bradshaw, Andrew Crites (who wrote Exercise 7.5), Michael Goff, Dustin Moody, and Koopa Koo wrote most of the solutions included in Chapter Solutions to Selected Exercises and found numerous typos throughout the book. Dustin Moody also carefully read through the book and provided feedback.
H. Stark suggested using Stirling’s formula in Section The Number of Digits of , and Mark Watkins and Lynn Walling made comments on Chapter Modular Forms of Weight 2.
Justin Walker found typos in the first published version of the book.
Parts of Chapter Modular Forms follow Serre’s beautiful introduction to modular forms [Ser73, Ch. VII] closely, though we adjust the notation, definitions, and order of presentation to be consistent with the rest of this book.
I would like to acknowledge the partial support of NSF Grant DMS 05-55776. Gunnells was supported in part by NSF Grants DMS 02-45580 and DMS 04-01525.
Notation and Conventions¶
We denote canonical isomorphisms by 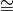 and noncanonical
isomorphisms by
and noncanonical
isomorphisms by 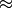 . If
. If  is a vector space and
is a vector space and  denotes
some sort of construction involving
denotes
some sort of construction involving  , we let
, we let 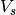 denote the
corresponding subspace and
denote the
corresponding subspace and 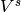 the quotient space. E.g., if
the quotient space. E.g., if  is an involution of
is an involution of  , then
, then 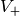 is
is 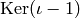 and
and
 . If
. If  is a finite abelian group, then
is a finite abelian group, then 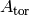 denotes the torsion subgroup and
denotes the torsion subgroup and 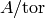 denotes the quotient
denotes the quotient
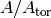 . We denote right group actions using exponential
notation. Everywhere in this book,
. We denote right group actions using exponential
notation. Everywhere in this book,  is a positive integer and
is a positive integer and  is an integer.
is an integer.
If  is an integer, a divisor
is an integer, a divisor 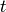 of
of  is a positive
integer such that
is a positive
integer such that 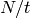 is an integer.
is an integer.