Modular Forms of Weight 2¶
We saw in Chapter Modular Forms of Level 1 (especially
Section Structure Theorem for Level 1 Modular Forms) that we can compute each space
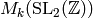 explicitly. This involves computing Eisenstein
series
explicitly. This involves computing Eisenstein
series 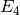 and
and 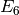 to some precision, then forming the basis
to some precision, then forming the basis
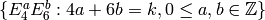 for
for 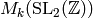 .
In this chapter we consider the more general problem of computing
.
In this chapter we consider the more general problem of computing
 , for any positive integer
, for any positive integer  . Again we have a
decomposition
. Again we have a
decomposition
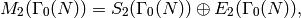
where 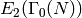 is spanned by generalized
Eisenstein
series and
is spanned by generalized
Eisenstein
series and  is the space of cusp forms,
i.e., elements of
is the space of cusp forms,
i.e., elements of 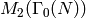 that vanish at all cusps.
that vanish at all cusps.
In Chapter Eisenstein Series and Bernoulli Numbers we compute the space 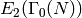 in a similar way to how we computed
in a similar way to how we computed 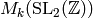 . On the other
hand, elements of
. On the other
hand, elements of  often cannot be written as sums
or products of generalized Eisenstein series. In fact, the structure
of
often cannot be written as sums
or products of generalized Eisenstein series. In fact, the structure
of 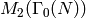 is, in general, much more complicated than that
of
is, in general, much more complicated than that
of 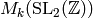 . For example, when
. For example, when  is a prime,
is a prime,
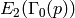 has dimension
has dimension  , whereas
, whereas 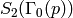 has dimension about
has dimension about 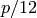 .
.
Fortunately an idea of Birch, which he called modular symbols, provides a
method for computing  and indeed for much more
that is relevant to understanding special values of
and indeed for much more
that is relevant to understanding special values of  -functions.
Modular symbols are also a powerful theoretical tool. In this
chapter, we explain how
-functions.
Modular symbols are also a powerful theoretical tool. In this
chapter, we explain how  is related to modular
symbols and how to use this relationship to explicitly compute a
basis for
is related to modular
symbols and how to use this relationship to explicitly compute a
basis for  . In Chapter General Modular Symbols we will
introduce more general modular symbols and explain how to use them to
compute
. In Chapter General Modular Symbols we will
introduce more general modular symbols and explain how to use them to
compute 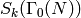 ,
, 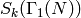 and
and 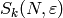 for
any integers
for
any integers 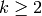 and
and  and character
and character  .
.
Section Hecke Operators contains a very brief summary of basic facts
about modular forms of weight  , modular curves, Hecke operators,
and integral homology. Section Modular Symbols introduces modular
symbols and describes how to compute with them. In
Section Computing the Boundary Map we talk about how to cut out the
subspace of modular symbols corresponding to cusp forms using the
boundary map. Section Computing a Basis for is about a straightforward
method to compute a basis for
, modular curves, Hecke operators,
and integral homology. Section Modular Symbols introduces modular
symbols and describes how to compute with them. In
Section Computing the Boundary Map we talk about how to cut out the
subspace of modular symbols corresponding to cusp forms using the
boundary map. Section Computing a Basis for is about a straightforward
method to compute a basis for  using modular
symbols, and Section Computing Using Eigenvectors outlines a more
sophisticated algorithm for computing newforms that uses
Atkin-Lehner theory.
using modular
symbols, and Section Computing Using Eigenvectors outlines a more
sophisticated algorithm for computing newforms that uses
Atkin-Lehner theory.
Before reading this chapter, you should have read Chapter Modular Forms and Chapter Modular Forms of Level 1. We also assume familiarity with algebraic curves, Riemann surfaces, and homology groups of compact Riemann surfaces.
Hecke Operators¶
Recall from Chapter Modular Forms that the group  acts on
acts on 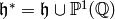 by linear fractional transformations.
The quotient
by linear fractional transformations.
The quotient 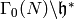 is a Riemann surface, which
we denote by
is a Riemann surface, which
we denote by 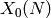 . See [DS05, Ch. 2] for a
detailed description of the topology on
. See [DS05, Ch. 2] for a
detailed description of the topology on 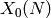 . The Rieman surface
. The Rieman surface
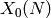 also has a canonical structure of algebraic curve over
also has a canonical structure of algebraic curve over  ,
as is explained in [DS05, Ch. 7] (see also
[Shi94, Section 6.7]).
,
as is explained in [DS05, Ch. 7] (see also
[Shi94, Section 6.7]).
Recall from Section Modular Forms of Any Level that a cusp form of weight  for
for  is a function
is a function  on
on  such that
such that 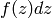 defines
a holomorphic differential on
defines
a holomorphic differential on 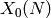 .
Equivalently, a cusp form is a holomorphic function
.
Equivalently, a cusp form is a holomorphic function  on
on  such
that
such
that
- the expression
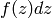 is invariant
under replacing
is invariant
under replacing  by
by 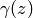 for each
for each 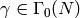 and
and 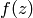 vanishes at every cusp for
vanishes at every cusp for  .
.
The space  of weight
of weight  cusp forms on
cusp forms on  is a finite-dimensional complex vector space, of dimension equal to
the genus
is a finite-dimensional complex vector space, of dimension equal to
the genus  of
of 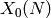 . The space
. The space 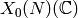 is a compact
oriented Riemann surface, so it is a
is a compact
oriented Riemann surface, so it is a  -dimensional oriented real
manifold, i.e.,
-dimensional oriented real
manifold, i.e., 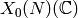 is a
is a  -holed torus (see
Figure 3.1).
-holed torus (see
Figure 3.1).
Condition (b) in the definition of  means that
means that  has a Fourier
expansion about each element of
has a Fourier
expansion about each element of 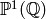 . Thus, at
. Thus, at  we have
we have
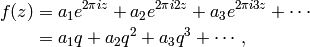
where, for brevity, we write 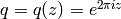 .
.
Example 3.1
Let  be the elliptic curve defined by the equation
be the elliptic curve defined by the equation
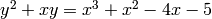 .
Let
.
Let 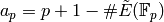 , where
, where 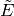 is the reduction of
is the reduction of  mod
mod  (note that for the
primes that divide the conductor of
(note that for the
primes that divide the conductor of  we have
we have 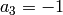 ,
, 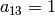 ).2
For
).2
For  composite, define
composite, define 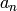 using the relations at the
end of Section Computing Using Eigenvectors.
using the relations at the
end of Section Computing Using Eigenvectors.
Then the Shimura-Taniyama conjecture asserts that
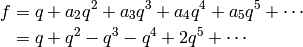
is the  -expansion of an element of
-expansion of an element of 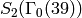 . This
conjecture, which is now a theorem (see
[BCDT01]), asserts that any
. This
conjecture, which is now a theorem (see
[BCDT01]), asserts that any
 -expansion constructed as above from an elliptic curve over
-expansion constructed as above from an elliptic curve over  is a modular form. This conjecture was mostly proved first by
Wiles [Wil95] as a key step in the proof of Fermat’s
last theorem.
is a modular form. This conjecture was mostly proved first by
Wiles [Wil95] as a key step in the proof of Fermat’s
last theorem.
Just as is the case for level  modular forms (see
Section Hecke Operators) there are commuting Hecke operators
modular forms (see
Section Hecke Operators) there are commuting Hecke operators 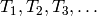 that act on
that act on  . To define them
conceptually, we introduce an interpretation of the modular curve
. To define them
conceptually, we introduce an interpretation of the modular curve
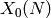 as an object whose points parameterize elliptic curves
with extra structure.
as an object whose points parameterize elliptic curves
with extra structure.
Proposition 3.2
The complex points of
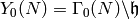 are in natural bijection with
isomorphism classes of pairs
are in natural bijection with
isomorphism classes of pairs 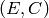 , where
, where  is an elliptic
curve over
is an elliptic
curve over  and
and  is a cyclic subgroup of
is a cyclic subgroup of 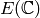 of
order
of
order  . The class of the point
. The class of the point 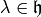 corresponds to
the pair
corresponds to
the pair
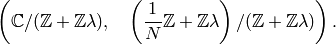
Proof
See Exercise 3.1.
Suppose  and
and  are coprime positive integers. There are two
natural maps
are coprime positive integers. There are two
natural maps 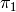 and
and 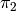 from
from 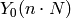 to
to 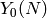 ; the
first,
; the
first, 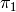 , sends
, sends 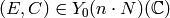 to
to 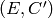 , where
, where
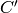 is the unique cyclic subgroup of
is the unique cyclic subgroup of  of order
of order  , and the
second,
, and the
second, 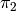 , sends
, sends 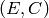 to
to 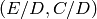 , where
, where  is the
unique cyclic subgroup of
is the
unique cyclic subgroup of  of order
of order  . These maps extend in a
unique way to algebraic maps from
. These maps extend in a
unique way to algebraic maps from 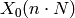 to
to 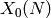 :
:
(1)![\xymatrix{ & X_0(n\cdot N) \ar[dl]_{\pi_2}\ar[dr]^{\pi_1}\\
X_0(N) & & X_0(N).}](_images/math/93b0b68694aa8ee4b37d3a3dec9f4ac500068856.png)
The 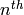 Hecke operator
Hecke operator  is
is 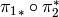 ,
where
,
where 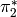 and
and 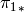 denote pullback and pushforward
of differentials, respectively. (There is a similar definition
of
denote pullback and pushforward
of differentials, respectively. (There is a similar definition
of  when
when 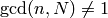 .)
Using our interpretation of
.)
Using our interpretation of  as differentials
on
as differentials
on 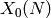 , this gives an action of Hecke operators on
, this gives an action of Hecke operators on  .
One can show that these induce the maps of Proposition 2.31
on
.
One can show that these induce the maps of Proposition 2.31
on  -expansions.
-expansions.
Example 3.3
There is a basis of 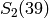 so that
so that
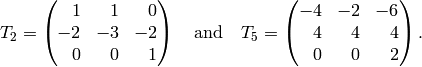
Notice that these matrices commute. Also, the characteristic
polynomial of  is
is 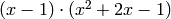 .
.
Homology¶
The first homology group 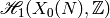 is the group of closed
is the group of closed
 -cycles modulo boundaries of
-cycles modulo boundaries of  -cycles (formal sums of images of
-cycles (formal sums of images of
 -simplexes). Topologically
-simplexes). Topologically 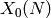 is a
is a  -holed torus,
where
-holed torus,
where  is the genus of
is the genus of 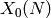 . Thus
. Thus 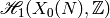 is a free
abelian group of rank
is a free
abelian group of rank 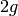 (see, e.g.,
[Gre81, Ex. 19.30] and [DS05, Section 6.1]),
with two generators corresponding to each hole, as illustrated in the
case
(see, e.g.,
[Gre81, Ex. 19.30] and [DS05, Section 6.1]),
with two generators corresponding to each hole, as illustrated in the
case 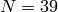 in Figure 3.1.
in Figure 3.1.
Figure 3.1
The homology of 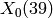
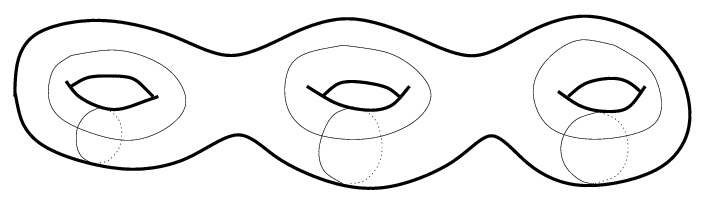
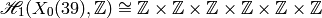
The homology of  is closely related to modular forms, since
the Hecke operators
is closely related to modular forms, since
the Hecke operators  also act on
also act on 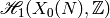 . The action
is by pullback of homology classes by
. The action
is by pullback of homology classes by 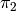 followed by taking the
image under
followed by taking the
image under 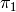 , where
, where 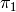 and
and 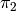 are as in
(1).
are as in
(1).
Integration defines a pairing
(2)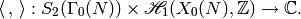
Explicitly, for a path  ,
,
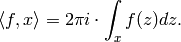
Theorem 3.4
The pairing (2) is nondegenerate and Hecke
equivariant in the sense that for every Hecke operator  , we
have
, we
have 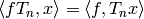 .
Moreover, it induces a perfect pairing
.
Moreover, it induces a perfect pairing
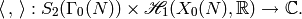
This is a special case of the results in Section Pairing Modular Symbols and Modular Forms.
As we will see, modular symbols allow us to make explicit the action
of the Hecke operators on 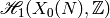 ; the above pairing then
translates this into a wealth of information about cusp forms.
; the above pairing then
translates this into a wealth of information about cusp forms.
We will also consider the relative homology group
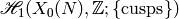 of
of 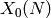 relative to the cusps; it is the same as usual homology, but i
n addition we allow paths with endpoints in the cusps instead of
restricting to closed loops. Modular symbols provide a
“combinatorial” presentation of
relative to the cusps; it is the same as usual homology, but i
n addition we allow paths with endpoints in the cusps instead of
restricting to closed loops. Modular symbols provide a
“combinatorial” presentation of 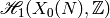 in terms of paths
between elements of
in terms of paths
between elements of 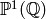 .
.
Modular Symbols¶
Let 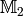 be the free abelian group with basis the set of symbols
be the free abelian group with basis the set of symbols
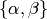 with
with 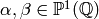 modulo the 3-term
relations
modulo the 3-term
relations
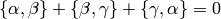
above and modulo any torsion. Since 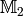 is torsion-free, we have
is torsion-free, we have

Warning
The symbols 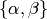 satisfy the relations
satisfy the relations
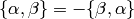 , so order matters. The
notation
, so order matters. The
notation 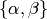 looks like the set containing two
elements, which strongly (and incorrectly) suggests that the order
does not matter. This is the standard notation in the literature.
looks like the set containing two
elements, which strongly (and incorrectly) suggests that the order
does not matter. This is the standard notation in the literature.
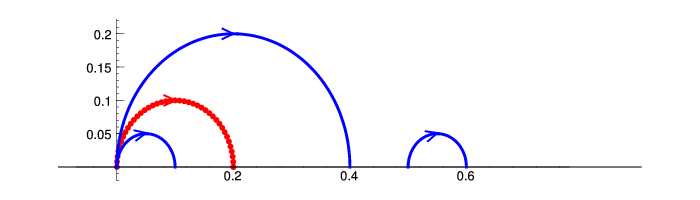
Figure 3.2
The modular symbols 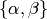 and
and 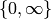
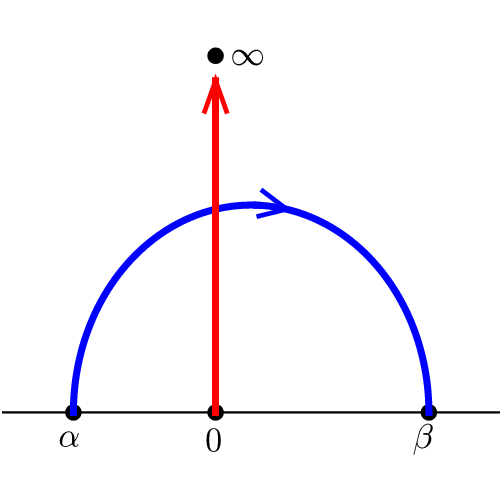
As illustrated in Figure 3.2, we “think of” this
modular symbol as the homology class, relative to the cusps, of a path
from 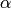 to
to 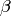 in
in 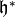 .
.
Define a left action of 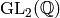 on
on 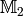 by letting
by letting
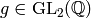 act by
act by
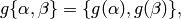
and  acts on
acts on 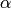 and
and 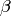 via the corresponding linear
fractional transformation. The space
via the corresponding linear
fractional transformation. The space 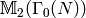 of
modular symbols for `\Gamma_0(N)` is the quotient of
of
modular symbols for `\Gamma_0(N)` is the quotient of 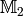 by the submodule generated by the infinitely many elements of the form
by the submodule generated by the infinitely many elements of the form
 , for
, for  in
in 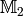 and
and  in
in  , and modulo
any torsion. A modular symbol for
, and modulo
any torsion. A modular symbol for  is an element of this
space. We frequently denote the equivalence class of a modular symbol
by giving a representative element.
is an element of this
space. We frequently denote the equivalence class of a modular symbol
by giving a representative element.
Example 3.6
Some modular symbols are  no matter what the level
no matter what the level  is! For
example, since
is! For
example, since 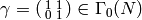 , we have
, we have
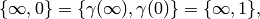
so
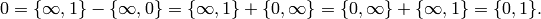
See Exercise 3.2 for a generalization of this observation.
There is a natural homomorphism
(3)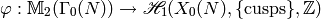
that sends a formal linear combination of geodesic paths in the upper
half plane to their image as paths on 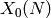 . In
[Man72] Manin proved that (3) is an
isomorphism (this is a fairly involved topological argument).
. In
[Man72] Manin proved that (3) is an
isomorphism (this is a fairly involved topological argument).
Manin identified the subspace of 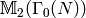 that is
sent isomorphically onto
that is
sent isomorphically onto 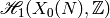 . Let
. Let 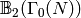 denote the free abelian group whose basis is the finite set
denote the free abelian group whose basis is the finite set
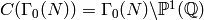 of cusps for
of cusps for
 . The boundary map
. The boundary map
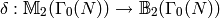
sends 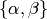 to
to 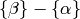 , where
, where 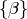 denotes the basis element of
denotes the basis element of 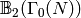 corresponding to
corresponding to
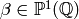 . The kernel
. The kernel 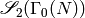 of
of 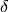 is
the subspace of cuspidal modular symbols. Thus an element of
is
the subspace of cuspidal modular symbols. Thus an element of
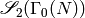 can be thought of as a linear combination of
paths in
can be thought of as a linear combination of
paths in 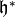 whose endpoints are cusps and whose images in
whose endpoints are cusps and whose images in 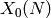 are homologous to a
are homologous to a  -linear combination of closed paths.
-linear combination of closed paths.
Theorem 3.7
The map 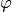 above induces a canonical isomorphism
above induces a canonical isomorphism
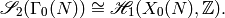
Proof
This is [Man72, Thm. 1.9].
For any (commutative) ring  let
let
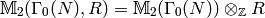
and
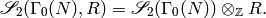
Proposition 3.8
We have
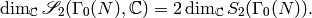
Proof
We have
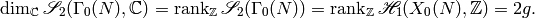
Example 3.9
We illustrate modular symbols in the case when 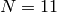 .
Using Sage (below),
which implements the algorithm that we describe below
over
.
Using Sage (below),
which implements the algorithm that we describe below
over  , we find that
, we find that 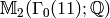 has basis
has basis
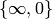 ,
, 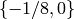 ,
, 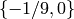 .
A basis for the integral homology
.
A basis for the integral homology 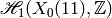 is the
subgroup generated by
is the
subgroup generated by 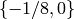 and
and 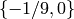 .
.
sage: set_modsym_print_mode ('modular')
sage: M = ModularSymbols(11, 2)
sage: M.basis()
({Infinity,0}, {-1/8,0}, {-1/9,0})
sage: S = M.cuspidal_submodule()
sage: S.integral_basis() # basis over ZZ.
({-1/8,0}, {-1/9,0})
sage: set_modsym_print_mode ('manin') # set it back
Computing with Modular Symbols¶
In this section, we describe a trick of Manin that we will use to prove that spaces of modular symbols are computable.
By Exercise 1.6 the group  has finite index in
has finite index in
 . Fix right coset representatives
. Fix right coset representatives 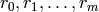 for
for  in
in  , so that
, so that
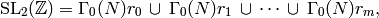
where the union is disjoint. For example, when  is prime, a list
of coset representatives is
is prime, a list
of coset representatives is
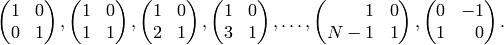
Let
(4)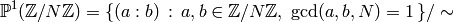
where 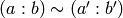 if there is
if there is 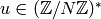 such
that
such
that 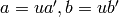 .
.
Proposition 3.10
There is a bijection between 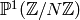 and the right cosets of
and the right cosets of
 in
in  , which sends a coset representative
, which sends a coset representative
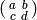 to the class of
to the class of 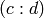 in
in 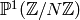 .
.
Proof
See Exercise 3.3.
See Proposition 1.27 for the analogous statement for
 .
.
We now describe an observation of Manin (see
[Man72, Section 1.5]) that is crucial to making
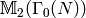 computable. It allows us to write any modular
symbol
computable. It allows us to write any modular
symbol 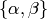 as a
as a  -linear combination of symbols of
the form
-linear combination of symbols of
the form 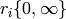 , where the
, where the 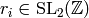 are coset
representatives as above. In particular, the finitely many symbols
are coset
representatives as above. In particular, the finitely many symbols
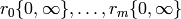 generate
generate
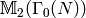 .
.
Proposition 3.11
[Manin]
Let  be a positive integer and
be a positive integer and 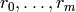 a set of right coset representatives for
a set of right coset representatives for  in
in
 .
Every
.
Every 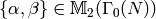 is a
is a  -linear combination of
-linear combination of
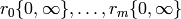 .
.
We give two proofs of the proposition. The first is useful for computation (see [Cre97a, Section 2.1.6]); the second (see [MTT86, Section 2]) is easier to understand conceptually since it does not require any knowledge of continued fractions.
Proof
Since
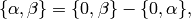
it suffices to consider modular symbols of the form 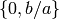 ,
where the rational number
,
where the rational number 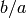 is in lowest terms. Expand
is in lowest terms. Expand 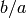 as a continued fraction and consider the successive convergents in
lowest terms:
as a continued fraction and consider the successive convergents in
lowest terms:
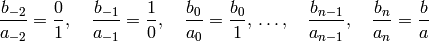
where the first two are included formally. Then
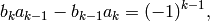
so that
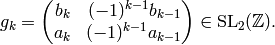
Hence
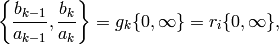
for some  , is of the required special form. Since
, is of the required special form. Since
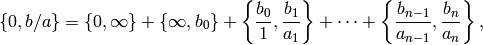
this completes the proof.
Proof
As in the first proof it suffices to prove the proposition for any
symbol 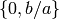 , where
, where 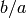 is in lowest terms. We will induct
on
is in lowest terms. We will induct
on 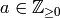 . If
. If 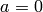 , then the symbol is
, then the symbol is 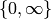 ,
which corresponds to the identity coset, so assume that
,
which corresponds to the identity coset, so assume that 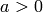 .
Find
.
Find 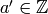 such that
such that
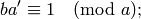
then 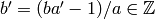 so the matrix
so the matrix
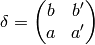
is an element of  . Thus
. Thus 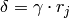 for
some right coset representative
for
some right coset representative 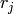 and
and 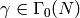 .
Then
.
Then
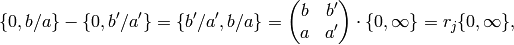
as elements of  . By induction,
. By induction,  is a linear combination of symbols of the form
is a linear combination of symbols of the form 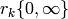 ,
which completes the proof.
,
which completes the proof.
Example 3.12
Let 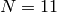 , and consider the modular symbol
, and consider the modular symbol 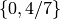 . We have
. We have
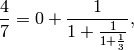
so the partial convergents are
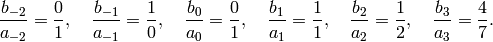
Thus, noting as in Example 3.6 that 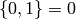 , we have
, we have
![\begin{eqnarray*}
\{0,4/7\} &=& \{0,\infty\} +\{\infty,0\} + \{0,1\}+ \{1,1/2\} + \{1/2,4/7\}\\
&=& \mtwo{1}{-1}{2}{-1}\{0,\infty\} + \mtwo{4}{1}{7}{2}\{0,\infty\}\\
&=& \mtwo{1}{0}{9}{1}\{0,\infty\} + \mtwo{1}{0}{9}{1}\{0,\infty\}\\
&=& 2 \cdot \left[\mtwo{1}{0}{9}{1}\{0,\infty\}\right].
\end{eqnarray*}](_images/math/df96b4bedffaa381a0cf8fea7e2730d49221792f.png)
We compute the convergents of 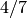 in Sage as follows (note that
in Sage as follows (note that
 and
and  are excluded):
are excluded):
sage: convergents(4/7)
[0, 1, 1/2, 4/7]
Manin Symbols¶
As above, fix coset representatives 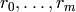 for
for  in
in  . Consider formal symbols
. Consider formal symbols ![[r_i]'](_images/math/f3248949fbd8d814e87d3d0ee027b42e504ca808.png) for
for 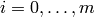 .
Let
.
Let ![[r_i]](_images/math/fe4443b5e0c478b5971e9b38e034df52a2f22276.png) be the modular symbol
be the modular symbol
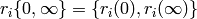 .
We equip the symbols
.
We equip the symbols ![[r_0]',\ldots,[r_m]'](_images/math/5a510fd2153554e9897e39bab594c9a5447f3a8e.png) with a
right action of
with a
right action of  , which is given by
, which is given by
![[r_i]'.g = [r_j]'](_images/math/b9e5c5c32284dd34d95e519e4ed74f9af75c78fd.png) , where
, where 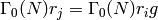 .
We extend the notation by writing
.
We extend the notation by writing
![[\gamma]' = [\Gamma_0(N)\gamma]' = [r_i]'](_images/math/6344e12d876553fc2b8949edd7855edb688694a7.png) , where
, where
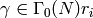 . Then the right action of
. Then the right action of
 is simply
is simply ![[\gamma]'.g = [\gamma g]'](_images/math/91e87d8b819a512de5abcdc06e927e7cdefac8dc.png) .
.
Theorem 1.2 implies that  is generated by the two matrices
is generated by the two matrices
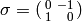 and
and
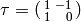 .
Note that
.
Note that 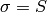 from Theorem 1.2 and
from Theorem 1.2 and
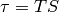 , so
, so 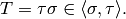
The following theorem provides us with a finite presentation for the
space 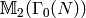 of modular symbols.
of modular symbols.
Theorem 3.13
Consider the quotient  of the free abelian group
on Manin symbols
of the free abelian group
on Manin symbols ![[r_0]',\ldots,[r_m]'](_images/math/5a510fd2153554e9897e39bab594c9a5447f3a8e.png) by the subgroup
generated by the elements (for all
by the subgroup
generated by the elements (for all  ):
):
![{[r_i]'} + [r_i]'\sigma \qquad\text{ and }\qquad
{[r_i]'} + [r_i]'\tau + [r_i]'\tau^2 ,](_images/math/314bcd4d1b1a3da3c8673fd0949c6cf0aaacbde2.png)
and modulo any torsion. Then there is an isomorphism
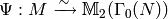
given by ![[r_i]' \mapsto [r_i] = r_i \{0,\infty\}](_images/math/48095e5042e5406e0abc8d3999248bad3b9f93bb.png) .
.
Proof
We will only prove that
is surjective; the proof that
is injective requires much more work and will be omitted from this book (see [Man72, Section 1.7] for a complete proof).
Proposition 3.11 implies that
is surjective, assuming that
is well defined. We next verify that
is well defined, i.e., that the listed 2-term and 3-term relations hold in the image. To see that the first relation holds, note that
![{[r_i]} + [r_i]\sigma
&= \{r_i(0),r_i(\infty)\} + \{r_i\sigma(0), r_i\sigma(\infty)\}\\
&= \{r_i(0),r_i(\infty)\} + \{r_i(\infty), r_i(0)\} \\
& = 0.](_images/math/4e1a9e5b6492798d9aa7533f3aff8946aec06721.png)
For the second relation we have
![{[r_i]} + [r_i]\tau + [r_i]\tau^2 &=
\{r_i(0),r_i(\infty)\} + \{r_i\tau(0), r_i\tau(\infty)\}
+ \{r_i\tau^2(0), r_i\tau^2(\infty)\} \\
&= \{r_i(0),r_i(\infty)\} + \{r_i(\infty), r_i(1)\}
+ \{r_i(1), r_i(0)\} \\
&= 0.](_images/math/edbcf86ebcfd0afea244a72363786025454a9c94.png)
Example 3.14
By default Sage computes modular symbols spaces over  , i.e.,
, i.e.,
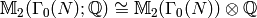 .
Sage represents (weight
.
Sage represents (weight  ) Manin symbols as pairs
) Manin symbols as pairs 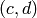 .
Here
.
Here 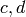 are integers that satisfy
are integers that satisfy 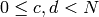 ; they define a point
; they define a point
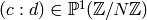 , hence a right coset of
, hence a right coset of  in
in  (see Proposition 3.10).
(see Proposition 3.10).
Create 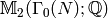 in Sage by typing
ModularSymbols(N, 2).
We then use the Sage command manin_generators to enumerate a list
of generators
in Sage by typing
ModularSymbols(N, 2).
We then use the Sage command manin_generators to enumerate a list
of generators ![[r_0], \ldots, [r_n]](_images/math/3c45597884fce84747ca09bba717f6137f2368f3.png) as in
Theorem 3.13 for several spaces of modular symbols.
as in
Theorem 3.13 for several spaces of modular symbols.
sage: M = ModularSymbols(2,2)
sage: M
Modular Symbols space of dimension 1 for Gamma_0(2)
of weight 2 with sign 0 over Rational Field
sage: M.manin_generators()
[(0,1), (1,0), (1,1)]
sage: M = ModularSymbols(3,2)
sage: M.manin_generators()
[(0,1), (1,0), (1,1), (1,2)]
sage: M = ModularSymbols(6,2)
sage: M.manin_generators()
[(0,1), (1,0), (1,1), (1,2), (1,3), (1,4), (1,5), (2,1),
(2,3), (2,5), (3,1), (3,2)]
Given x=(c,d), the command x.lift_to_sl2z(N)
computes an element of  whose lower two entries are
congruent to
whose lower two entries are
congruent to 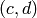 modulo
modulo  .
.
sage: M = ModularSymbols(2,2)
sage: [x.lift_to_sl2z(2) for x in M.manin_generators()]
[[1, 0, 0, 1], [0, -1, 1, 0], [0, -1, 1, 1]]
sage: M = ModularSymbols(6,2)
sage: x = M.manin_generators()[9]
sage: x
(2,5)
sage: x.lift_to_sl2z(6)
[1, 2, 2, 5]
The manin_basis command returns a list of indices into the
Manin generator list such that the corresponding symbols form a basis
for the quotient of the  -vector space spanned by Manin symbols
modulo the
-vector space spanned by Manin symbols
modulo the  -term and
-term and  -term relations of
Theorem 3.13.
-term relations of
Theorem 3.13.
sage: M = ModularSymbols(2,2)
sage: M.manin_basis()
[1]
sage: [M.manin_generators()[i] for i in M.manin_basis()]
[(1,0)]
sage: M = ModularSymbols(6,2)
sage: M.manin_basis()
[1, 10, 11]
sage: [M.manin_generators()[i] for i in M.manin_basis()]
[(1,0), (3,1), (3,2)]
Thus, e.g., every element of 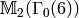 is a
is a  -linear
combination of the three symbols
-linear
combination of the three symbols ![[(1,0)]](_images/math/005384eaf1021152f7921bf2a923d964820a6c4f.png) ,
, ![[(3,1)]](_images/math/1df5ca8552c5b09e03a0362de6a171f8db359db8.png) , and
, and ![[(3,2)]](_images/math/0aebb25edfc0cf432472353596c2a84cb3266ff1.png) .
We can write each of these as a modular symbol using the
modular_symbol_rep function.
.
We can write each of these as a modular symbol using the
modular_symbol_rep function.
sage: M.basis()
((1,0), (3,1), (3,2))
sage: [x.modular_symbol_rep() for x in M.basis()]
[{Infinity,0}, {0,1/3}, {-1/2,-1/3}]
The manin_gens_to_basis function returns a matrix whose rows express each Manin symbol generator in terms of the subset of Manin symbols that forms a basis (as returned by manin_basis).
sage: M = ModularSymbols(2,2)
sage: M.manin_gens_to_basis()
[-1]
[ 1]
[ 0]
Since the basis is 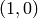 , this
means that in
, this
means that in 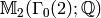 , we have
, we have
![[(0,1)] = -[(1,0)]](_images/math/6582a8bd0f0f9a02824c5b4306bb8d472b4adb65.png) and
and ![[(1,1)] = 0](_images/math/95dd5c55ac10e04864384dc8a5e4e618e7c66ccd.png) .
(Since no denominators are involved, we have in
fact computed a presentation of
.
(Since no denominators are involved, we have in
fact computed a presentation of 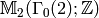 .)
.)
To convert a Manin symbol 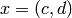 to an element of a modular
symbols space
to an element of a modular
symbols space  , use M(x):
, use M(x):
sage: M = ModularSymbols(2,2)
sage: x = (1,0); M(x)
(1,0)
Next consider 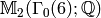 :
:
sage: M = ModularSymbols(6,2)
sage: M.manin_gens_to_basis()
[-1 0 0]
[ 1 0 0]
[ 0 0 0]
[ 0 -1 1]
[ 0 -1 0]
[ 0 -1 1]
[ 0 0 0]
[ 0 1 -1]
[ 0 0 -1]
[ 0 1 -1]
[ 0 1 0]
[ 0 0 1]
Recall that our choice of basis for
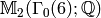 is
is ![[(1,0)], [(3,1)], [(3,2)]](_images/math/8efdf6ef121de6e6fc109b3e2d44f8b69d57e292.png) .
Thus, e.g., the first row of this matrix says that
.
Thus, e.g., the first row of this matrix says that
![[(0,1)] = -[(1,0)]](_images/math/6582a8bd0f0f9a02824c5b4306bb8d472b4adb65.png) , and the fourth row asserts
that
, and the fourth row asserts
that
![[(1,2)] = -[(3,1)] + [(3,2)]](_images/math/8e42a6f9fd473ddf5d7b6bb2fa5f1922eee4f720.png) .
.
sage: M = ModularSymbols(6,2)
sage: M((0,1))
-(1,0)
sage: M((1,2))
-(3,1) + (3,2)
Hecke Operators¶
Hecke Operators on Modular Symbols¶
When  is a prime not dividing
is a prime not dividing  , define
, define
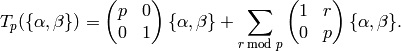
The Hecke operators are compatible with
the integration pairing 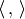 of Section Hecke Operators, in the
sense that
of Section Hecke Operators, in the
sense that 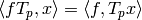 .
When
.
When 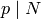 , the definition is the same, except that the matrix
, the definition is the same, except that the matrix
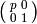 is not included in the sum (see Theorem 1.44).
There is a similar definition of
is not included in the sum (see Theorem 1.44).
There is a similar definition of  for
for  composite
(see Section General Definition of Hecke Operators).
composite
(see Section General Definition of Hecke Operators).
Hecke Operators on Manin Symbols¶
In [Mer94], L. Merel gives a description of the action of
 directly on Manin symbols
directly on Manin symbols ![[r_i]](_images/math/fe4443b5e0c478b5971e9b38e034df52a2f22276.png) (see
Section Hecke Operators on Manin Symbols for details). For example, when
(see
Section Hecke Operators on Manin Symbols for details). For example, when
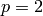 and
and  is odd, we have
is odd, we have
(5)![T_2([r_i]) = [r_i]\mtwo{1}{0}{0}{2} + [r_i]\mtwo{2}{0}{0}{1}
+ [r_i]\mtwo{2}{1}{0}{1} + [r_i]\mtwo{1}{0}{1}{2}.](_images/math/c3beb09711fdba7ff18c3132ac76eaccb85be341.png)
For any prime, let 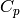 be the set of matrices
constructed using the following algorithm (see [Cre97a, Section 2.4]):
be the set of matrices
constructed using the following algorithm (see [Cre97a, Section 2.4]):
Algorithm 3.16
Given a prime  , this algorithm outputs a list of
, this algorithm outputs a list of 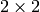 matrices of determinant
matrices of determinant  that can be used to compute the Hecke
operator
that can be used to compute the Hecke
operator  .
.
- Output
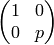 .
. - For
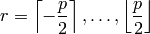 :
:- Let
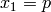 ,
, 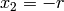 ,
, 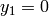 ,
, 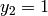 ,
, 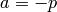 ,
, 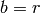 .
. - Output
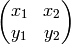 .
. - As long as
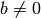 , do the following:
, do the following:- Let
 be the integer closest to
be the integer closest to 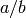 (if
(if 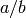 is a half
integer, round away from
is a half
integer, round away from  ).
). - Let
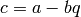 ,
, 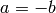 ,
, 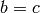 .
. - Set
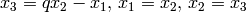 , and\
, and\
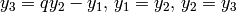 .
. - Output
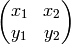 .
.
- Let
- Let
Proposition 3.17
Let 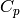 be as above. Then
for
be as above. Then
for 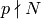 and
and ![[x]\in \M_2(\Gamma_0(N))](_images/math/dc5f4d802ae7e3f9db73ae5789bf8e4a90a6ea6a.png) a Manin
symbol, we have
a Manin
symbol, we have
![T_p([x]) = \sum_{g \in C_p} [xg].](_images/math/4e86f4de5c3602361f5f70a6dc2a0bfae5df56d6.png)
Proof
See Proposition~2.4.1 of [Cre97a].
There are other lists of matrices, due to Merel, that work even when
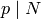 (see Section Hecke Operators on Manin Symbols).
(see Section Hecke Operators on Manin Symbols).
The command HeilbronnCremonaList(p), for  prime,
outputs the list of matrices from Algorithm 3.16.
prime,
outputs the list of matrices from Algorithm 3.16.
sage: HeilbronnCremonaList(2)
[[1, 0, 0, 2], [2, 0, 0, 1], [2, 1, 0, 1], [1, 0, 1, 2]]
sage: HeilbronnCremonaList(3)
[[1, 0, 0, 3], [3, 1, 0, 1], [1, 0, 1, 3], [3, 0, 0, 1],
[3, -1, 0, 1], [-1, 0, 1, -3]]
sage: HeilbronnCremonaList(5)
[[1, 0, 0, 5], [5, 2, 0, 1], [2, 1, 1, 3], [1, 0, 3, 5],
[5, 1, 0, 1], [1, 0, 1, 5], [5, 0, 0, 1], [5, -1, 0, 1],
[-1, 0, 1, -5], [5, -2, 0, 1], [-2, 1, 1, -3],
[1, 0, -3, 5]]
sage: len(HeilbronnCremonaList(37))
128
sage: len(HeilbronnCremonaList(389))
1892
sage: len(HeilbronnCremonaList(2003))
11662
.. index::
pair: Sage; Hecke operator `T_2`
Example 3.18
We compute the matrix of
on
:
sage: M = ModularSymbols(2,2) sage: M.T(2).matrix() [1]
Example 3.19
We compute some Hecke operators on 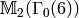 :
:
sage: M = ModularSymbols(6, 2)
sage: M.T(2).matrix()
[ 2 1 -1]
[-1 0 1]
[-1 -1 2]
sage: M.T(3).matrix()
[3 2 0]
[0 1 0]
[2 2 1]
sage: M.T(3).fcp() # factored characteristic polynomial
(x - 3) * (x - 1)^2
For 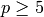 we have
we have 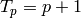 , since
, since 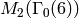 is
spanned by generalized Eisenstein series (see Chapter Eisenstein Series and Bernoulli Numbers).
is
spanned by generalized Eisenstein series (see Chapter Eisenstein Series and Bernoulli Numbers).
Example 3.20
We compute the Hecke operators on 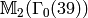 :
:
sage: M = ModularSymbols(39, 2)
sage: T2 = M.T(2)
sage: T2.matrix()
[ 3 0 -1 0 0 1 1 -1 0]
[ 0 0 2 0 -1 1 0 1 -1]
[ 0 1 0 -1 1 1 0 1 -1]
[ 0 0 1 0 0 1 0 1 -1]
[ 0 -1 2 0 0 1 0 1 -1]
[ 0 0 1 1 0 1 1 -1 0]
[ 0 0 0 -1 0 1 1 2 0]
[ 0 0 0 1 0 0 2 0 1]
[ 0 0 -1 0 0 0 1 0 2]
sage: T2.fcp() # factored characteristic polynomial
(x - 3)^3 * (x - 1)^2 * (x^2 + 2*x - 1)^2
The Hecke operators commute, so their eigenspace structures are related.
sage: T2 = M.T(2).matrix()
sage: T5 = M.T(5).matrix()
sage: T2*T5 - T5*T2 == 0
True
sage: T5.charpoly().factor()
(x^2 - 8)^2 * (x - 6)^3 * (x - 2)^2
The decomposition of  is a list of the kernels of
is a list of the kernels of
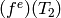 , where
, where  runs through the irreducible factors of the
characteristic polynomial of
runs through the irreducible factors of the
characteristic polynomial of  and
and 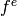 exactly divides this
characteristic polynomial. Using Sage, we find them:
exactly divides this
characteristic polynomial. Using Sage, we find them:
sage: M = ModularSymbols(39, 2)
sage: M.T(2).decomposition()
[
Modular Symbols subspace of dimension 3 of Modular
Symbols space of dimension 9 for Gamma_0(39) of weight
2 with sign 0 over Rational Field,
Modular Symbols subspace of dimension 2 of Modular
Symbols space of dimension 9 for Gamma_0(39) of weight
2 with sign 0 over Rational Field,
Modular Symbols subspace of dimension 4 of Modular
Symbols space of dimension 9 for Gamma_0(39) of weight
2 with sign 0 over Rational Field
]
Computing the Boundary Map¶
In Section Modular Symbols we defined a map 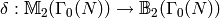 . The kernel of this map is the space
. The kernel of this map is the space
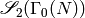 of cuspidal modular symbols. This kernel will be
important in computing cusp forms in Section Computing Using Eigenvectors
below.
of cuspidal modular symbols. This kernel will be
important in computing cusp forms in Section Computing Using Eigenvectors
below.
To compute the boundary map on ![[\gamma]](_images/math/4756ff3495c9a43e708269fd762f9b77339fd0fd.png) , note
that
, note
that ![[\gamma] = \{\gamma(0),\gamma(\infty)\}](_images/math/88b0dfa921d478637ebe6cb685d6c248eaffa652.png) , so
if
, so
if 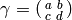 , then
, then
![\delta([\gamma]) = \{\gamma(\infty)\} - \{\gamma(0)\}
= \{a/c\} - \{b/d\}.](_images/math/4f1b8b8260da346a5863b213d5f033abb44935ec.png)
Computing this boundary map would appear to first require an algorithm
to compute the set 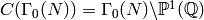 of cusps for
of cusps for  . In fact, there is a trick that computes the
set of cusps in the course of running the algorithm. First, give an
algorithm for deciding whether or not two elements of
. In fact, there is a trick that computes the
set of cusps in the course of running the algorithm. First, give an
algorithm for deciding whether or not two elements of 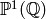 are
equivalent modulo the action of
are
equivalent modulo the action of  . Then simply construct
. Then simply construct
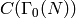 in the course of computing the boundary map, i.e.,
keep a list of cusps found so far, and whenever a new cusp class is
discovered, add it to the list. The following proposition,
which is proved in [Cre97a, Prop. 2.2.3], explains how to determine
whether two cusps are equivalent.
in the course of computing the boundary map, i.e.,
keep a list of cusps found so far, and whenever a new cusp class is
discovered, add it to the list. The following proposition,
which is proved in [Cre97a, Prop. 2.2.3], explains how to determine
whether two cusps are equivalent.
Proposition 3.21
Let
,
, be pairs of integers with
and possibly
. There is
such that
in
if and only if
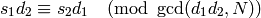
where
satisfies
.
In Sage the command boundary_map() computes the boundary map from
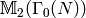 to
to 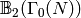 , and the
cuspidal_submodule
command computes its kernel. For example, for level
, and the
cuspidal_submodule
command computes its kernel. For example, for level  the boundary
map is given by the matrix
the boundary
map is given by the matrix ![[1 \,\,\, -1]](_images/math/289456ab0271b46cfd3b30d735cb66a958cb784b.png) , and its kernel is the
, and its kernel is the  space:
space:
sage: M = ModularSymbols(2, 2)
sage: M.boundary_map()
Hecke module morphism boundary map defined by the matrix
[ 1 -1]
Domain: Modular Symbols space of dimension 1 for
Gamma_0(2) of weight ...
Codomain: Space of Boundary Modular Symbols for
Congruence Subgroup Gamma0(2) ...
sage: M.cuspidal_submodule()
Modular Symbols subspace of dimension 0 of Modular
Symbols space of dimension 1 for Gamma_0(2) of weight
2 with sign 0 over Rational Field
The smallest level for which the boundary map has nontrivial kernel,
i.e., for which 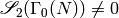 , is
, is 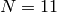 .
.
sage: M = ModularSymbols(11, 2)
sage: M.boundary_map().matrix()
[ 1 -1]
[ 0 0]
[ 0 0]
sage: M.cuspidal_submodule()
Modular Symbols subspace of dimension 2 of Modular
Symbols space of dimension 3 for Gamma_0(11) of weight
2 with sign 0 over Rational Field
sage: S = M.cuspidal_submodule(); S
Modular Symbols subspace of dimension 2 of Modular
Symbols space of dimension 3 for Gamma_0(11) of weight
2 with sign 0 over Rational Field
sage: S.basis()
((1,8), (1,9))
The following illustrates that the
Hecke operators preserve 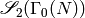 :
:
sage: S.T(2).matrix()
[-2 0]
[ 0 -2]
sage: S.T(3).matrix()
[-1 0]
[ 0 -1]
sage: S.T(5).matrix()
[1 0]
[0 1]
A nontrivial fact is that for  prime the eigenvalue of each
of these matrices is
prime the eigenvalue of each
of these matrices is 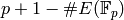 , where
, where  is the
elliptic curve
is the
elliptic curve 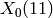 defined by the (affine) equation
defined by the (affine) equation
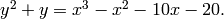 For example, we have
For example, we have
sage: E = EllipticCurve([0,-1,1,-10,-20])
sage: 2 + 1 - E.Np(2)
-2
sage: 3 + 1 - E.Np(3)
-1
sage: 5 + 1 - E.Np(5)
1
sage: 7 + 1 - E.Np(7)
-2
The same numbers appear as the eigenvalues of Hecke operators:
sage: [S.T(p).matrix()[0,0] for p in [2,3,5,7]]
[-2, -1, 1, -2]
In fact, something similar happens for every elliptic curve over  .
The book [DS05] (especially Chapter~8) is about this
striking numerical relationship between the number of
points on elliptic curves
modulo
.
The book [DS05] (especially Chapter~8) is about this
striking numerical relationship between the number of
points on elliptic curves
modulo  and coefficients of modular forms.
and coefficients of modular forms.
Computing a Basis for  ¶
¶
This section is about a method for using modular symbols to compute a
basis for  . It is not the most efficient for
certain applications, but it is easy to explain and understand.
See Section Computing Using Eigenvectors for a method that takes
advantage of additional structure of
. It is not the most efficient for
certain applications, but it is easy to explain and understand.
See Section Computing Using Eigenvectors for a method that takes
advantage of additional structure of  .
.
Let 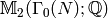 and
and 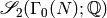 be the spaces
of modular symbols and cuspidal modular symbols over
be the spaces
of modular symbols and cuspidal modular symbols over  . Before we begin, we
describe a simple but crucial fact about the relation between cusp
forms and Hecke operators.
. Before we begin, we
describe a simple but crucial fact about the relation between cusp
forms and Hecke operators.
If ![f = \sum b_n q^n \in \C[[q]]](_images/math/df86b830092c8c05f69a5ad5905a1ad9e853d5f5.png) is a power series,
let
is a power series,
let 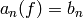 be the
be the  coefficient of
coefficient of  .
Notice that
.
Notice that 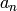 is a
is a  -linear map
-linear map ![\C[[q]] \to \C](_images/math/183a7465166004a287e3b88972d0ac97edff76a5.png) .
.
As explained in [DS05, Prop. 5.3.1] and
[Lan95, Section VII.3] (recall also Proposition 2.31), the
Hecke operators  act on elements of
act on elements of
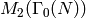 as follows (where
as follows (where  below):
below):
(6)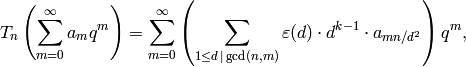
where  if
if 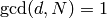 and
and 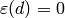 if
if 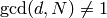 .
(Note: More generally, if
.
(Note: More generally, if 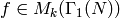 is a modular form
with Dirichlet character
is a modular form
with Dirichlet character  , then the above formula holds; above
we are considering this formula in the special case when
, then the above formula holds; above
we are considering this formula in the special case when  is the trivial character and
is the trivial character and 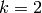 .)
.)
Lemma 3.22
Suppose ![f\in \C[[q]]](_images/math/8d373177e7654788e4a74a16ab2e79eed865cabc.png) and
and  is a positive integer. Let
is a positive integer. Let  be the operator on
be the operator on  -expansions (formal power series) defined
by (6). Then
-expansions (formal power series) defined
by (6). Then
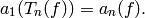
Proof
The coefficient of  in (6) is
in (6) is
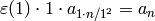 .
.
The Hecke algebra  is the ring generated by all
Hecke operators
is the ring generated by all
Hecke operators  acting on
acting on  .
Let
.
Let 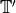 denote the image of the Hecke algebra in
denote the image of the Hecke algebra in
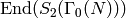 , and let
, and let 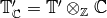 be the
be the
 -span of the Hecke operators. Let
-span of the Hecke operators. Let 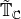 denote the subring of
denote the subring of
![\End(\C[[q]])](_images/math/28a77ebd9dfdae567caf26cab073ac97cd74cbc6.png) generated over
generated over  by all Hecke operators acting on
formal power series via definition (6).
by all Hecke operators acting on
formal power series via definition (6).
Proposition 3.23
There is a bilinear pairing of complex vector spaces
![\C[[q]] \cross \tT_\C \to \C](_images/math/6a8a1a6ccbec94885ad94cd2bd081cd3f6c9db84.png)
given by
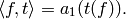
If  is such that
is such that 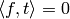 for
all
for
all 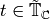 , then
, then 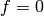 .
.
Proof
The pairing is bilinear since both 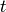 and
and 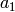 are linear.
are linear.
Suppose ![f\in \C[[q]]](_images/math/8d373177e7654788e4a74a16ab2e79eed865cabc.png) is such that
is such that
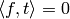 for all
for all 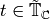 .
Then
.
Then 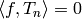 for each positive integer
for each positive integer  .
But by Lemma 3.22 we have
.
But by Lemma 3.22 we have
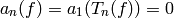
for all  ; thus
; thus 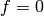 .
.
Proposition 3.24
There is a perfect bilinear pairing of complex vector spaces
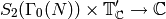
given by
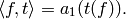
Proof
The pairing has  kernel on the left by
Proposition 3.23.
Suppose that
kernel on the left by
Proposition 3.23.
Suppose that 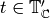 is such that
is such that
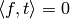 for all
for all 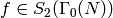 .
Then
.
Then 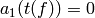 for all
for all  . For any
. For any  , the image
, the image
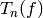 is also a cusp form, so
is also a cusp form, so 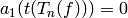 for all
for all  and
and  . Finally the fact that
. Finally the fact that 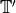 is commutative
and Lemma 3.22 together imply that for all
is commutative
and Lemma 3.22 together imply that for all  and
and  ,
,
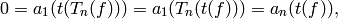
so 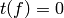 for all
for all  . Thus
. Thus 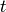 is the
is the  operator.
operator.
Since  has finite dimension and the
kernel on each side of the pairing is
has finite dimension and the
kernel on each side of the pairing is  , it follows
that the pairing is perfect, i.e., defines an isomorphism
, it follows
that the pairing is perfect, i.e., defines an isomorphism
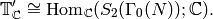
By Proposition 3.24 there is an isomorphism of vector spaces
(7)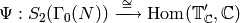
that sends 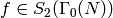 to the homomorphism
to the homomorphism
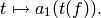
For any  -linear map
-linear map 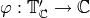 , let
, let
![f_{\vphi} = \sum_{n=1}^{\infty} \vphi(T_n)q^n \in\C[[q]].](_images/math/5c54da2f9b30367ba6be9c4e21b630b435465ca2.png)
Lemma 3.25
The series  is the
is the  -expansion of
-expansion of
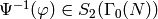 .
.
Proof
Note that it is not even a priori obvious that 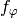 is the
is the  -expansion of a modular form.
Let
-expansion of a modular form.
Let 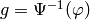 , which is by definition the unique element of
, which is by definition the unique element of
 such that
such that 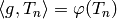 for all
for all  .
By Lemma 3.22, we have
.
By Lemma 3.22, we have
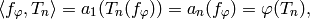
so 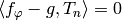 for all
for all  .
Proposition 3.23 implies that
.
Proposition 3.23 implies that
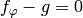 , so
, so 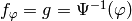 ,
as claimed.
,
as claimed.
Conclusion:
The cusp forms 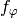 , as
, as 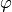 varies through a
basis of
varies through a
basis of 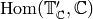 , form a basis
for
, form a basis
for  .
In particular, we can compute
.
In particular, we can compute  by computing
by computing 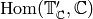 , where we compute
, where we compute 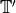 in any way we want,
e.g., using a space that contains an isomorphic copy of
in any way we want,
e.g., using a space that contains an isomorphic copy of  .
.
Algorithm 3.26
Given positive integers  and
and  , this algorithm computes
a basis for
, this algorithm computes
a basis for  to precision
to precision 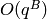 .
.
Compute
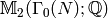 via the presentation of Section Manin Symbols.
via the presentation of Section Manin Symbols.Compute the subspace
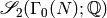 of cuspidal modular symbols as in Section
Computing the Boundary Map.
of cuspidal modular symbols as in Section
Computing the Boundary Map.Let
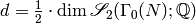 .
By Proposition 3.8,
.
By Proposition 3.8,
 is the dimension of
is the dimension of  .
.Let
![[T_n]](_images/math/0e7499846655165c5bb785955c70dd211f67c03c.png) denote the matrix of
denote the matrix of  acting on a basis of
acting on a basis of
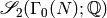 . For a matrix
. For a matrix  , let
, let 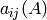 denote the
denote the 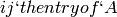 . For various integers
. For various integers 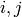 with
with
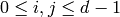 , compute formal
, compute formal  -expansions
-expansions![f_{ij}(q) = \sum_{n=1}^{B-1} a_{ij}([T_n])q^n + O(q^{B}) \in \Q[[q]]](_images/math/edc238989b55e6e7c670fc261339dfe6c475b644.png)
until we find enough to span a space of dimension
 (or
exhaust all of them). These
(or
exhaust all of them). These 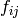 are a basis for
are a basis for
 to precision
to precision 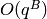 .
.
Examples¶
We use Sage to demonstrate Algorithm 3.26.
Example 3.27
The smallest  with
with 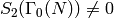 is
is 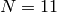 .
.
sage: M = ModularSymbols(11); M.basis()
((1,0), (1,8), (1,9))
sage: S = M.cuspidal_submodule(); S
Modular Symbols subspace of dimension 2 of Modular
Symbols space of dimension 3 for Gamma_0(11) of weight
2 with sign 0 over Rational Field
We compute a few Hecke operators, and then read off a
nonzero cusp form, which forms a basis for 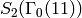 :
:
sage: S.T(2).matrix()
[-2 0]
[ 0 -2]
sage: S.T(3).matrix()
[-1 0]
[ 0 -1]
Thus
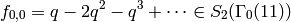
forms a basis for 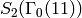 .
.
Example 3.28
We compute a basis for 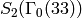 to precision
to precision 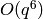 .
.
sage: M = ModularSymbols(33)
sage: S = M.cuspidal_submodule(); S
Modular Symbols subspace of dimension 6 of Modular
Symbols space of dimension 9 for Gamma_0(33) of weight
2 with sign 0 over Rational Field
Example 3.29
Next consider 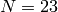 , where we have
, where we have
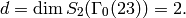
The command q_expansion_cuspforms computes
matrices  and returns a function
and returns a function
 such that
such that 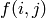 is the
is the  -expansion of
-expansion of
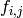 to some precision.
(For efficiency reasons,
to some precision.
(For efficiency reasons, 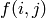 in Sage actually
computes matrices of
in Sage actually
computes matrices of  acting
on a basis for the linear dual of
acting
on a basis for the linear dual of 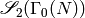 .)
.)
sage: M = ModularSymbols(23)
sage: S = M.cuspidal_submodule()
sage: S
Modular Symbols subspace of dimension 4 of Modular
Symbols space of dimension 5 for Gamma_0(23) of weight
2 with sign 0 over Rational Field
sage: f = S.q_expansion_cuspforms(6)
sage: f(0,0)
q - 2/3*q^2 + 1/3*q^3 - 1/3*q^4 - 4/3*q^5 + O(q^6)
sage: f(0,1)
O(q^6)
sage: f(1,0)
-1/3*q^2 + 2/3*q^3 + 1/3*q^4 - 2/3*q^5 + O(q^6)
Thus a basis for 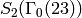 is
is
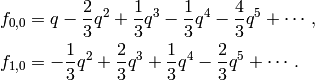
Or, in echelon form,
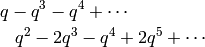
which we computed using
sage: S.q_expansion_basis(6)
[
q - q^3 - q^4 + O(q^6),
q^2 - 2*q^3 - q^4 + 2*q^5 + O(q^6)
]
Computing  Using Eigenvectors¶
Using Eigenvectors¶
In this section we describe how to use modular symbols to construct a
basis of  consisting of modular forms that are
eigenvectors for every element of the ring
consisting of modular forms that are
eigenvectors for every element of the ring 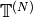 generated by the
Hecke operator
generated by the
Hecke operator  , with
, with 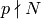 . Such eigenvectors are called
eigenforms.
. Such eigenvectors are called
eigenforms.
Suppose  is a positive integer that divides
is a positive integer that divides  . As explained in
[Lan95, VIII.1–2], for each divisor
. As explained in
[Lan95, VIII.1–2], for each divisor  of
of 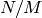 there is
a natural degeneracy map
there is
a natural degeneracy map 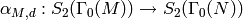 given by
given by 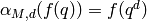 . The
new subspace of
. The
new subspace of  , denoted
, denoted
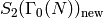 , is the complementary
, is the complementary  -submodule of the
-submodule of the
 -module generated by the images of all maps
-module generated by the images of all maps 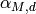 ,
with
,
with  and
and  as above. It is a nontrivial fact that this
complement is well defined; one possible proof uses the Petersson
inner product (see [Lan95, Section VII.5]).
as above. It is a nontrivial fact that this
complement is well defined; one possible proof uses the Petersson
inner product (see [Lan95, Section VII.5]).
The theory of Atkin and Lehner [AL70] (see
Theorem 9.4 below) asserts that, as a 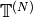 -module,
-module,
 decomposes as follows:
decomposes as follows:

To compute  it suffices to compute
it suffices to compute
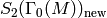 for each
for each 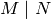 .
.
We now turn to the problem of computing 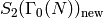 .
Atkin and Lehner [AL70] proved that
.
Atkin and Lehner [AL70] proved that
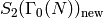 is spanned by eigenforms for all
is spanned by eigenforms for all  with
with
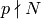 and that the common eigenspaces of all the
and that the common eigenspaces of all the  with
with
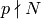 each have dimension
each have dimension  . Moreover, if
. Moreover, if 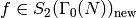 is an eigenform then the coefficient of
is an eigenform then the coefficient of  in the
in the  -expansion of
-expansion of  is nonzero, so it is possible to
normalize
is nonzero, so it is possible to
normalize  so the coefficient of
so the coefficient of  is
is  (such a
normalized eigenform in the new subspace is called a
newform). With
(such a
normalized eigenform in the new subspace is called a
newform). With  so normalized, if
so normalized, if 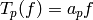 , then
the
, then
the 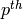 Fourier coefficient of
Fourier coefficient of  is
is 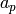 . If
. If
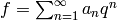 is a normalized eigenvector for all
is a normalized eigenvector for all
 , then the
, then the 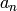 , with
, with  composite, are determined by the
composite, are determined by the
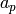 , with
, with  prime, by the following formulas:
prime, by the following formulas: 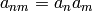 when
when  and
and  are relatively prime and
are relatively prime and 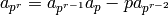 for
for 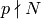 prime. When
prime. When 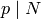 ,
,
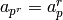 . We conclude that in order to compute
. We conclude that in order to compute
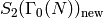 , it suffices to compute all systems of
eigenvalues
, it suffices to compute all systems of
eigenvalues 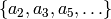 of the prime-indexed Hecke
operators
of the prime-indexed Hecke
operators 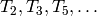 acting on
acting on 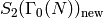 .
Given a system of eigenvalues, the corresponding eigenform is
.
Given a system of eigenvalues, the corresponding eigenform is
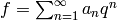 , where the
, where the 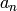 , for
, for  composite,
are determined by the recurrence given above.
composite,
are determined by the recurrence given above.
In light of the pairing 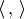 introduced in
Section Hecke Operators,
computing the above systems of eigenvalues
introduced in
Section Hecke Operators,
computing the above systems of eigenvalues 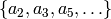 amounts to computing the systems of eigenvalues of the Hecke operators
amounts to computing the systems of eigenvalues of the Hecke operators
 on the subspace
on the subspace  of
of 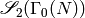 that corresponds
to the new subspace of
that corresponds
to the new subspace of 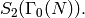 For each proper divisor
For each proper divisor  of
of  and each divisor
and each divisor  of
of
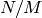 , let
, let 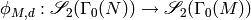 be the map
sending
be the map
sending  to
to 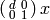 .
Then
.
Then  is the intersection of the kernels of all
maps
is the intersection of the kernels of all
maps 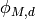 .
.
Computing the systems of eigenvalues of a collection of commuting diagonalizable endomorphisms is a problem in linear algebra (see Chapter Linear Algebra).
Example 3.30
All forms in 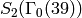 are new.
Up to Galois conjugacy, the eigenvalues of the Hecke operators
are new.
Up to Galois conjugacy, the eigenvalues of the Hecke operators
 ,
, 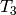 ,
, 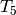 , and
, and 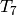 on
on 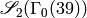 are
are
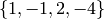 and
and 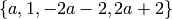 , where
, where
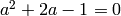 . Each of these eigenvalues occur
in
. Each of these eigenvalues occur
in 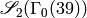 with multiplicity two; for example,
the characteristic polynomial of
with multiplicity two; for example,
the characteristic polynomial of  on
on 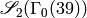 is
is
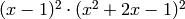 .
Thus
.
Thus 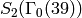 is spanned by
is spanned by
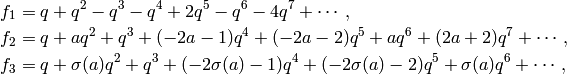
where 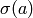 is the other
is the other 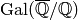 -conjugate of
-conjugate of  .
.
Summary¶
To compute the  -expansion of a basis for
-expansion of a basis for  , we use
the degeneracy maps so that we only have to solve the problem for
, we use
the degeneracy maps so that we only have to solve the problem for
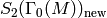 , for all integers
, for all integers 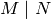 . Using modular
symbols, we compute all systems of eigenvalues
. Using modular
symbols, we compute all systems of eigenvalues
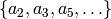 , and then write down the corresponding
eigenforms
, and then write down the corresponding
eigenforms 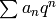 .
.
Exercises¶
Exercise 3.1
Suppose that 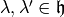 are in the same orbit for
the action of
are in the same orbit for
the action of  , i.e., that there exists
, i.e., that there exists
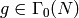 such that
such that 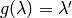 . Let
. Let
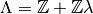 and
and 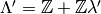 .
Prove that the pairs
.
Prove that the pairs
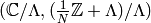 and
and
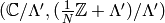 are
isomorphic.
(By an isomorphism
are
isomorphic.
(By an isomorphism 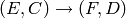 of pairs, we mean an
isomorphism
of pairs, we mean an
isomorphism 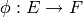 of elliptic curves that sends
of elliptic curves that sends  to
to
 . You may use the fact that an isomorphism of elliptic curves
over
. You may use the fact that an isomorphism of elliptic curves
over  is a
is a  -linear map
-linear map 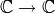 that sends the lattice
corresponding to one curve onto the lattice corresponding to the
other.)
that sends the lattice
corresponding to one curve onto the lattice corresponding to the
other.)
Exercise 3.2
Let 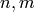 be integers and
be integers and  a positive integer. Prove that the
modular symbol
a positive integer. Prove that the
modular symbol 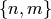 is
is  as an element of
as an element of
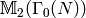 . [Hint: See Example 3.6.]
. [Hint: See Example 3.6.]
Exercise 3.3
Let  be a prime.
be a prime.
- List representative elements of
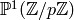 .
. - What is the cardinality of
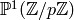 as a function of
as a function of  ?
? - Prove that there is a bijection between the right cosets of
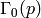 in
in  and the elements of
and the elements of 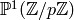 that sends
that sends 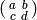 to
to 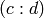 . (As mentioned in
this chapter, the analogous statement is also true when the
level is composite; see [Cre97a, Section 2.2] for
complete details.) end{enumerate}
. (As mentioned in
this chapter, the analogous statement is also true when the
level is composite; see [Cre97a, Section 2.2] for
complete details.) end{enumerate}
Exercise 3.4
Use the inductive proof of Proposition 3.11 to write
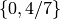 in terms of Manin symbols for
in terms of Manin symbols for 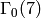 .
.
Exercise 3.5
Show that the Hecke operator  acts as multiplication
by
acts as multiplication
by  on the space
on the space 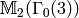 as follows:
as follows:
- Write down right coset representatives for
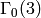 in
in  .
. - List all eight relations coming from Theorem 3.13.
- Find a single Manin symbols
![[r_i]](_images/math/fe4443b5e0c478b5971e9b38e034df52a2f22276.png) so that the three other
Manin symbols are a nonzero multiple of
so that the three other
Manin symbols are a nonzero multiple of ![[r_i]](_images/math/fe4443b5e0c478b5971e9b38e034df52a2f22276.png) modulo the
relations found in the previous step.
modulo the
relations found in the previous step. - Use formula (5) to compute
![T_2([r_i])](_images/math/763be4a6ceaad6949c8165c288985a2bd694aa68.png) . You will
obtain a sum of four symbols. Using the relations above, write
this sum as a multiple of
. You will
obtain a sum of four symbols. Using the relations above, write
this sum as a multiple of ![[r_i]](_images/math/fe4443b5e0c478b5971e9b38e034df52a2f22276.png) . (The multiple must be
. (The multiple must be  or
you made a mistake.)
or
you made a mistake.)
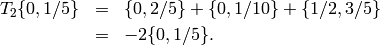
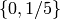 under
under