Eisenstein Series and Bernoulli Numbers¶
We introduce generalized Bernoulli numbers attached to Dirichlet
characters and give an algorithm to enumerate the Eisenstein series
in 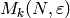 .
.
The Eisenstein Subspace¶
Let  be the space of modular forms of weight
be the space of modular forms of weight
 for
for  , and let
, and let  be the Hecke algebra
acting on
be the Hecke algebra
acting on  , which is the subring of
, which is the subring of
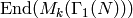 generated by all Hecke operators.
Then there is a
generated by all Hecke operators.
Then there is a  -module decomposition
-module decomposition
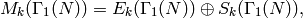
where 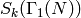 is the subspace of modular forms that vanish
at all cusps and
is the subspace of modular forms that vanish
at all cusps and 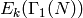 is the
Eisenstein subspace, which
is uniquely determined by this decomposition.
The above decomposition
induces a decomposition of
is the
Eisenstein subspace, which
is uniquely determined by this decomposition.
The above decomposition
induces a decomposition of 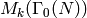 and of
and of
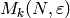 , for any Dirichlet character
, for any Dirichlet character  of modulus
of modulus  .
.
Generalized Bernoulli Numbers¶
Suppose  is a Dirichlet character of modulus
is a Dirichlet character of modulus  over
over  .
Leopoldt [Leo58] defined generalized Bernoulli
numbers attached to
.
Leopoldt [Leo58] defined generalized Bernoulli
numbers attached to  .
.
Definition 5.1
We define the generalized Bernoulli numbers 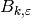 attached to
attached to  by the following
identity of infinite series:
by the following
identity of infinite series:
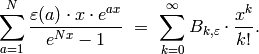
If  is the trivial character of modulus
is the trivial character of modulus  and
and 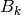 are as in Section Examples of Modular Forms of Level 1, then
are as in Section Examples of Modular Forms of Level 1, then
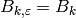 , except when
, except when 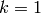 , in which case
, in which case
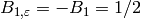 (see Exercise 5.2).
(see Exercise 5.2).
Algebraically Computing Generalized Bernoulli Numbers¶
Let 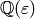 denote the field generated by the image
of the character
denote the field generated by the image
of the character  ; thus
; thus 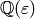 is the cyclotomic
extension
is the cyclotomic
extension 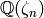 , where
, where  is the order of
is the order of  .
.
Algorithm 5.2
Given an integer 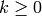 and any
Dirichlet character
and any
Dirichlet character  with modulus
with modulus  , this algorithm computes
the generalized Bernoulli numbers
, this algorithm computes
the generalized Bernoulli numbers  , for
, for 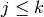 .
.
Compute
![g \set x/(e^{Nx}-1) \in \Q[[x]]](_images/math/e3ccc02e86e79f0780606f32c3509996e9dc4686.png) to precision
to precision
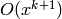 by computing
by computing 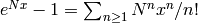 to precision
to precision 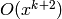 and computing the inverse
and computing the inverse
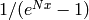 , then multiplying by
, then multiplying by  .
.For each
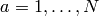 , compute
, compute
![f_a \set g \cdot e^{ax}\in\Q[[x]]](_images/math/742c91cb0d08254714f2d9d9b21cb609fd7718b1.png) , to precision
, to precision 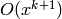 .
This requires computing
.
This requires computing 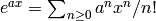 to
precision
to
precision 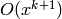 . (Omit computation of
. (Omit computation of 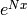 if
if 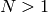 since then
since then 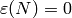 .)
.)Then for
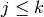 , we have
, we have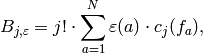
where
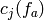 is the coefficient of
is the coefficient of 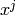 in
in 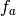 .
.
Note that in steps (1) and (2) we compute the
power series doing arithmetic only in ![\Q[[x]]](_images/math/562f19fccc5907ba1d5ca3413336c3eb4c8028d5.png) , not in
, not in
![\Q(\eps)[[x]]](_images/math/e65d36d686f8eb0476968bc1d6dde7b264effd93.png) , which could be much less efficient if
, which could be much less efficient if  has
large order. In step (1) if
has
large order. In step (1) if  is huge,
we could compute the inverse
is huge,
we could compute the inverse 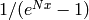 using
asymptotically fast arithmetic and
Newton iteration.
using
asymptotically fast arithmetic and
Newton iteration.
Example 5.3
The nontrivial character  with modulus
with modulus 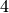 has order
has order  and takes values in
and takes values in  . The Bernoulli
numbers
. The Bernoulli
numbers 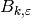 for
for  even are all
even are all  and for
and for  odd
they are
odd
they are
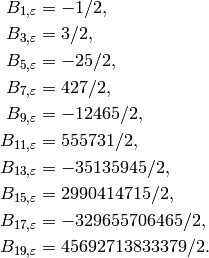
Example 5.4
The generalized Bernoulli numbers
need not be in  . Suppose
. Suppose  is the mod
is the mod 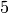 character
such that
character
such that 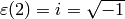 . Then
. Then 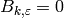 for
for  even
and
even
and

Example 5.5
We use Sage to compute some of the above generalized Bernoulli numbers.
First we define the character and verify that 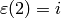 (note that
in Sage zeta4 is
(note that
in Sage zeta4 is 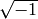 ).
).
sage: G = DirichletGroup(5)
sage: e = G.0
sage: e(2)
zeta4
We compute the Bernoulli number 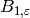 .
.
sage: e.bernoulli(1)
-1/5*zeta4 - 3/5
We compute 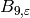 .
.
sage: e.bernoulli(9)
-108846/5*zeta4 - 176868/5
Proposition 5.6
If 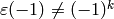 and
and 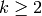 , then
, then 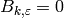 .
.
Proof
See Exercise 5.3.
Computing Generalized Bernoulli Numbers Analytically¶
This section, which was written jointly with Kevin McGown, is about a way to compute generalized Bernoulli numbers, which is similar to the algorithm in Section Fast Computation of Bernoulli Numbers.
Let 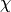 be a primitive Dirichlet character
modulo its conductor
be a primitive Dirichlet character
modulo its conductor  .
Note from the definition of Bernoulli numbers that
if
.
Note from the definition of Bernoulli numbers that
if 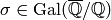 , then
, then
(1)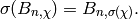
For any character 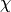 , we define the Gauss sum
, we define the Gauss sum 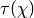 as
as
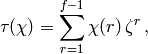
where 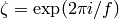 is the principal
is the principal 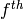 root of unity.
The Dirichlet
root of unity.
The Dirichlet  -function for
-function for 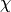 for
for 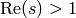 is
is
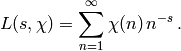
In the right half plane 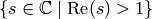 this function is analytic, and because
this function is analytic, and because 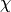 is
multiplicative, we have the Euler product representation
is
multiplicative, we have the Euler product representation
(2)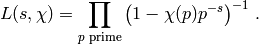
We note (but will not use) that through analytic continuation 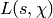 can be extended to a meromorphic function on the entire complex plane.
can be extended to a meromorphic function on the entire complex plane.
If 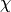 is a nonprincipal primitive Dirichlet character of
conductor
is a nonprincipal primitive Dirichlet character of
conductor  such that
such that 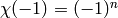 , then (see, e.g.,
[Wan82])
, then (see, e.g.,
[Wan82])
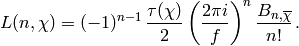
Solving for the Bernoulli number yields
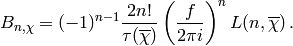
This allows us to give decimal approximations for 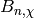 .
It remains to compute
.
It remains to compute 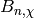 exactly (i.e., as an algebraic integer).
To simplify the above expression, we define
exactly (i.e., as an algebraic integer).
To simplify the above expression, we define
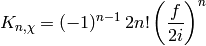
and write
(3)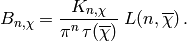
Note that we can compute 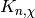 exactly in the field
exactly in the field
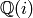 .
.
The following result
identifies the denominator of 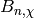 .
.
Theorem 5.7
Let  and
and 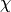 be as above, and
define an integer
be as above, and
define an integer  as follows:
as follows:
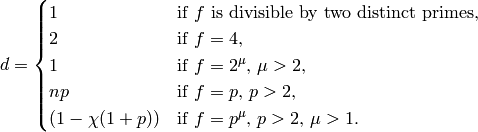
Then 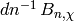 is integral.
is integral.
To compute the algebraic integer 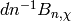 , and we compute
, and we compute
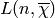 to very high precision using the Euler product
(2) and the formula (3). We carry out the
same computation for each of the
to very high precision using the Euler product
(2) and the formula (3). We carry out the
same computation for each of the 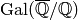 conjugates of
conjugates of
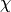 , which by (1) yields the conjugates of
, which by (1) yields the conjugates of
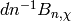 . We can then write down the characteristic
polynomial of
. We can then write down the characteristic
polynomial of 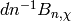 to very high precision and
recognize the coefficients as rational integers. Finally, we determine
which of the roots of the characteristic polynomial is
to very high precision and
recognize the coefficients as rational integers. Finally, we determine
which of the roots of the characteristic polynomial is  by approximating them all numerically to high precision
and seeing which is closest to our numerical approximation to
by approximating them all numerically to high precision
and seeing which is closest to our numerical approximation to
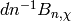 . The details are similar
to what is explained in Section Fast Computation of Bernoulli Numbers.
. The details are similar
to what is explained in Section Fast Computation of Bernoulli Numbers.
Explicit Basis for the Eisenstein Subspace¶
Suppose 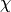 and
and 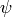 are primitive Dirichlet characters with
conductors
are primitive Dirichlet characters with
conductors  and
and  , respectively.
Let
, respectively.
Let
(4)![E_{k,\chi,\psi}(q) = c_0 + \sum_{m \geq 1} \left(
\sum_{n|m} \psi(n) \cdot \chi(m/n) \cdot n^{k-1}\right) q^{m}
\in \Q(\chi, \psi)[[q]],](_images/math/1a68b633092788869bfb04f62800fc4f2b2071f8.png)
where
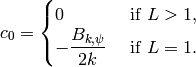
Note that when 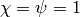 and
and 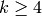 , then
, then 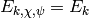 ,
where
,
where 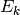 is from Chapter Modular Forms.
is from Chapter Modular Forms.
Miyake proves statements that imply the following in [Miy89, Ch. 7].
Theorem 5.8
Suppose 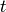 is a positive integer and
is a positive integer and 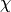 ,
, 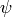 are as above
and that
are as above
and that  is a positive integer such that
is a positive integer such that 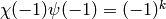 .
Except when
.
Except when 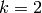 and
and 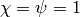 , the power series
, the power series
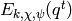 defines an element of
defines an element of
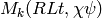 .
If
.
If 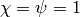 ,
, 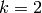 ,
, 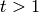 , and
, and 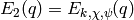 , then
, then
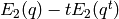 is a modular form in
is a modular form in 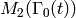 .
.
Theorem 5.9
The Eisenstein series in 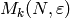 coming from
Theorem 5.8 with
coming from
Theorem 5.8 with 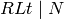 and
and 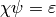 form a basis for the
Eisenstein subspace
form a basis for the
Eisenstein subspace 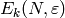 .
.
Theorem 5.10
The Eisenstein series
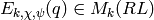 defined above
are eigenforms (i.e., eigenvectors for all Hecke operators
defined above
are eigenforms (i.e., eigenvectors for all Hecke operators  ).
Also
).
Also 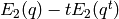 , for
, for 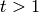 , is an eigenform.
, is an eigenform.
Since 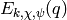 is normalized so the coefficient
of
is normalized so the coefficient
of  is
is  , the eigenvalue of
, the eigenvalue of 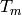 is the coefficient
is the coefficient
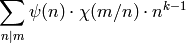
of 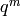 (see Proposition 9.10).
Also for
(see Proposition 9.10).
Also for 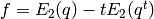 with
with 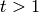 prime, the coefficient of
prime, the coefficient of  is
is  ,
, 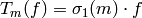 for
for 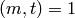 , and
, and 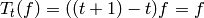 .
.
Algorithm 5.11
Given a weight  and a Dirichlet character
and a Dirichlet character  of modulus
of modulus  ,
this algorithm computes a basis for the Eisenstein
subspace
,
this algorithm computes a basis for the Eisenstein
subspace 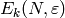 of
of 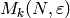 to precision
to precision 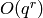 .
.
1. [Weight  Trivial Character?] If
Trivial Character?] If 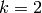 and
and 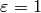 , output the
Eisenstein series
, output the
Eisenstein series 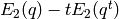 , for each divisor
, for each divisor 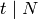 with
with 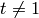 , and then terminate.
, and then terminate.
- [Empty Space?] If
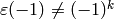 , output the empty list.
, output the empty list. - [Compute Dirichlet Group] Let
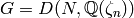 be the
group of Dirichlet characters with values in
be the
group of Dirichlet characters with values in 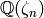 ,
where
,
where  is the exponent of
is the exponent of  .
. - [Compute Conductors] Compute the
conductor of every element of
 using
Algorithm 4.19.
using
Algorithm 4.19. - [List Characters
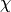 ] Form a list
] Form a list
 of all Dirichlet characters
of all Dirichlet characters 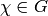 such that
such that
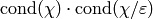 divides
divides  .
. - [Compute Eisenstein Series] For each character
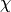 in
in  ,
let
,
let 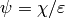 and compute
and compute
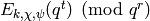 for each divisor
for each divisor 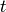 of
of
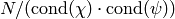 . Here we compute
. Here we compute
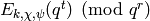 using (4) and
Algorithm 5.2.
using (4) and
Algorithm 5.2.
Remark 5.12
Algorithm 5.11 is what is currently used in Sage. It might be better to first reduce to the prime power case by writing all characters as a product of local characters and combine steps (4) and (5) into a single step that involves orders. However, this might make things more obscure.
Example 5.13
The following is a basis of Eisenstein series
for 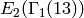 .
.
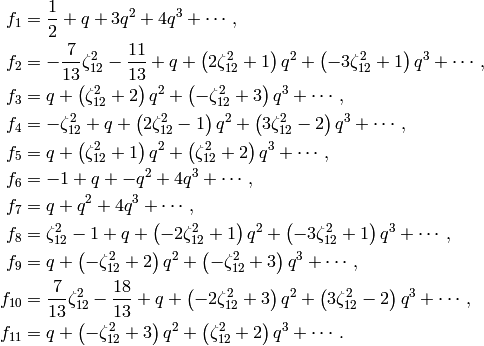
We computed it as follows:
sage: E = EisensteinForms(Gamma1(13),2)
sage: E.eisenstein_series()
We can also compute the parameters 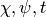 that
define each series:
that
define each series:
sage: e = E.eisenstein_series()
sage: for e in E.eisenstein_series():
... print e.parameters()
...
([1], [1], 13)
([1], [zeta6], 1)
([zeta6], [1], 1)
([1], [zeta6 - 1], 1)
([zeta6 - 1], [1], 1)
([1], [-1], 1)
([-1], [1], 1)
([1], [-zeta6], 1)
([-zeta6], [1], 1)
([1], [-zeta6 + 1], 1)
([-zeta6 + 1], [1], 1)
Exercises¶
Exercise 5.1
Suppose  and
and  are diagonalizable linear transformations of a
finite-dimensional vector space
are diagonalizable linear transformations of a
finite-dimensional vector space  over an algebraically closed
field
over an algebraically closed
field 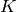 and that
and that 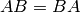 . Prove there is a basis for
. Prove there is a basis for  so that
the matrices of
so that
the matrices of  and
and  with respect to that basis are both
simultaneously diagonal.
with respect to that basis are both
simultaneously diagonal.
Exercise 5.2
If  is the trivial character of modulus
is the trivial character of modulus  and
and 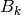 are as
in Section Examples of Modular Forms of Level 1, then
are as
in Section Examples of Modular Forms of Level 1, then 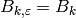 ,
except when
,
except when 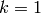 , in which case
, in which case 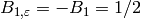 .
.
Exercise 5.3
Prove that for 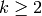 if
if 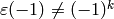 , then
, then
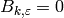 .
.
Exercise 5.4
Show that the dimension of the Eisenstein subspace
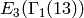 is
is 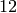 by finding a basis of series
by finding a basis of series
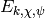 . You do not have to write down the
. You do not have to write down the
 -expansions of the series, but you do have to figure out which
-expansions of the series, but you do have to figure out which
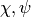 to use.
to use.