Solutions to Selected Exercises¶
Chapter 1¶
Exercise 1.1. Suppose
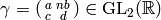 is a matrix
with positive determinant.
Then
is a matrix
with positive determinant.
Then 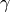 is a linear fractional transformation that fixes the
real line, so it must either fix or swap the upper and
lower half planes. Now
is a linear fractional transformation that fixes the
real line, so it must either fix or swap the upper and
lower half planes. Now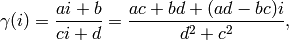
so since
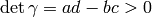 , the imaginary part of
, the imaginary part of 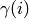 is positive; hence
is positive; hence 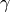 sends the upper half plane to itself.
sends the upper half plane to itself.Exercise 1.2. Avoiding poles, the quotient rule for differentiation goes through exactly as in the real case, so any rational function
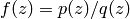 (
(![p,q \in \C[z]](_images/math/284cbd1d307ae0de21294d5784814264d863d14a.png) ) is holomorphic on
) is holomorphic on
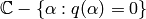 . By the fundamental theorem of
algebra, this set of poles is finite, and hence it is discrete.
Write
. By the fundamental theorem of
algebra, this set of poles is finite, and hence it is discrete.
Write 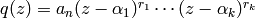 for
each
for
each 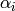 and let
and let 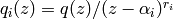 which is a
polynomial nonzero at
which is a
polynomial nonzero at 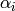 . Thus for each
. Thus for each  we have
we have
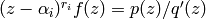 is holomorphic at
is holomorphic at 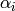 and hence
and hence 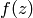 is meromorphic on
is meromorphic on  .
.-
The product
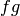 of two meromorphic functions on the upper half
plane is itself meromorphic. Also, for all
of two meromorphic functions on the upper half
plane is itself meromorphic. Also, for all 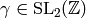 we have
we have![(fg)^{[\gamma]_{k+j}}
&= \frac{1}{(cz+d)^{k+j}}((fg) \circ \gamma)\\
&= \frac{1}{(cz+d)^k}(f \circ \gamma) \frac{1}{(cz+d)^j}(g \circ \gamma)
= fg,](_images/math/1c7e37205cd3ae1e6ee5b38d8d88e10f464ef384.png)
so
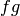 is weakly modular.
is weakly modular.If
 is meromorphic on the upper half plane, then so is
is meromorphic on the upper half plane, then so is 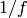 .
Now
.
Now![\qquad\qquad\frac{1}{f} = \frac{1}{(cz+d)^{-k} f \circ \gamma} = (cz+d)^k ((1/f) \circ \gamma) = \frac{1}{f}^{[\gamma]_{-k}},](_images/math/2cd91871aa958beb7d74a84ee7c6e5e53b28ea0c.png)
so
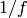 is a weakly modular form of weight
is a weakly modular form of weight 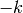 .
.Let
 and
and  be modular functions. Then, as above,
be modular functions. Then, as above, 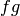 is a
weakly modular function. Let
is a
weakly modular function. Let 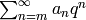 and
and
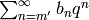 be their
be their  -expansions around any
-expansions around any
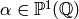 ; then their formal product is the
; then their formal product is the
 -expansion of
-expansion of 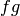 . But the formal product of two Laurant series
about the same point is itself a Laurant series with convergence in
the intersection of the convergent domains of the original series,
so
. But the formal product of two Laurant series
about the same point is itself a Laurant series with convergence in
the intersection of the convergent domains of the original series,
so 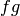 has a meromorphic
has a meromorphic  -expansion at each
-expansion at each 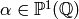 and hence at each cusp.
and hence at each cusp.We are in exactly the same case as in part (c), but because
 and
and  are modular functions,
are modular functions, 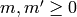 and hence the function
is holomorphic at each of its cusps.
and hence the function
is holomorphic at each of its cusps.
Exercise 1.4. Let
 be a weakly modular function of odd weight
be a weakly modular function of odd weight
 . Since
. Since
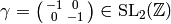 , we have
, we have 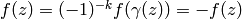 so
so 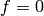 .
.Exercise 1.5. Because
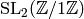 is the trivial group,
is the trivial group, 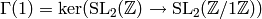 must be all of
must be all of
 . As
. As 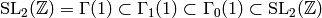 , we must have
, we must have 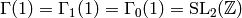 .
.-
- The group
 is the inverse image of
the subgroup of
is the inverse image of
the subgroup of 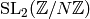 generated by
generated by 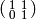 , and
the inverse image of a group (under a group homomorphism)
is a group.
, and
the inverse image of a group (under a group homomorphism)
is a group. - The group contains the kernel of the homomorphism
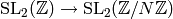 , and
that kernel has finite index since the quotient is
contained in
, and
that kernel has finite index since the quotient is
contained in 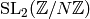 , which is finite.
, which is finite. - Same argument as previous part.
- The level is at most
 since both groups contain
since both groups contain 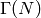 .
It can be no greater than
.
It can be no greater than  since
since 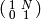 is in both
groups.
is in both
groups.
- The group
Exercise 1.7. See [DS05, Lemma 1.2.2].
Exercise 1.8. Let
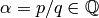 ,
where
,
where  and
and  are relatively prime. By the Euclidian
algorithm, we can find
are relatively prime. By the Euclidian
algorithm, we can find 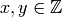 such that
such that 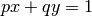 . Let
. Let
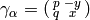 . Note that
. Note that 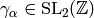 and
and 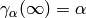 . Also let
. Also let
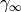 be the identity map on
be the identity map on 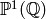 . Now
. Now
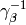 sends
sends 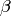 to
to  so we have
so we have
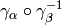 which sends
which sends 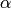 to
to
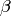 .
.
Chapter 2¶
Exercise 2.1. We have
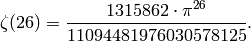
Variation: Compute
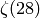 .
.Exercise 2.2. Omitted.
-
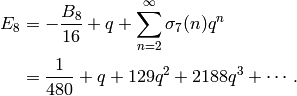
Variation: Compute
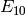 .
. Exercise 2.4. Omitted.
Exercise 2.5. We have
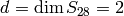 . A choice of
. A choice of
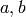 with
with 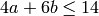 and
and 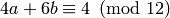 is
is 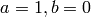 .
A basis for
.
A basis for 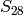 is then
is then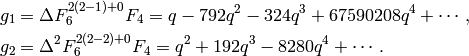
The Victor Miller basis is then
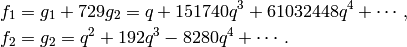
Variation: Compute the Victor Miller basis for
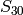 .
.Exercise 2.6. From the previous exercise we have
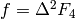 .
Then
.
Then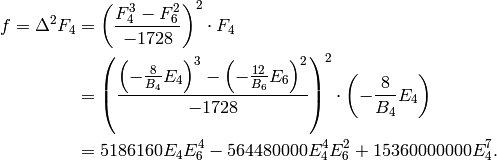
Exercise 2.7. No, it is not always integral. For example, for
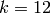 , the coefficient of
, the coefficient of  is
is 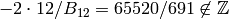 .
Variation: Find, with proof, the set of all
.
Variation: Find, with proof, the set of all  such that the normalized
series
such that the normalized
series 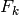 is integral (use that
is integral (use that 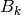 is eventually very
large compared to
is eventually very
large compared to 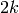 ).
).Exercise 2.8. We compute the Victor Miller basis to precision great enough to determine
 . This means
we need up to
. This means
we need up to 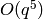 .
.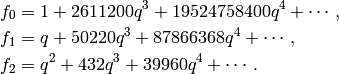
Then the matrix of
 on this basis is
on this basis is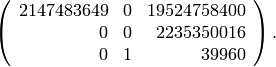
(The rows of this matrix are the linear combinations that give the images of the
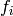 under
under  .)
This matrix has characteristic polynomial
.)
This matrix has characteristic polynomial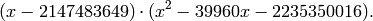
Chapter 3¶
Exercise 3.1. Write
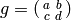 , so
, so
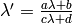 .
Let
.
Let  be the isomorphism
be the isomorphism 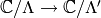 given by
given by 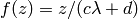 .
We have
.
We have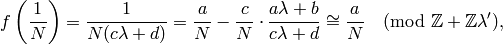
where the second equality can be verified easily by expanding out each side, and for the congruence we use that
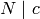 .
Thus the subgroup of
.
Thus the subgroup of 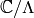 generated by
generated by 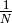 is
taken isomorphically to the subgroup of
is
taken isomorphically to the subgroup of 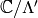 generated
by
generated
by 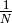 .
.Exercise 3.2. For any integer
 ,
we have
,
we have 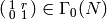 ,
so
,
so 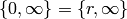 .
Thus
.
Thus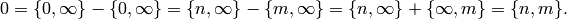
-
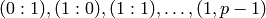 .
.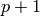 .
.- See [Cre97a, Prop. 2.2.1].
Exercise 3.4. We start with
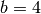 ,
, 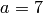 . Then
. Then 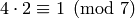 .
Let
.
Let 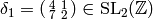 . Since
. Since
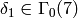 ,
we use the right coset representative
,
we use the right coset representative 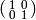 and see that
and see that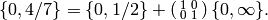
Repeating the process, we have
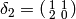 , which is
in the same coset at
, which is
in the same coset at 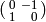 . Thus
. Thus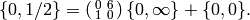
Putting it together gives
![\{0,4/7\} = \abcd{1}{0}{0}{1} \{0,\infty\} + \abcd{0}{6}{1}{0}\{0,\infty\}
= [(0,1)] + [(1,0)].](_images/math/e4d73a370da074dc014c29d67adb6192236ecfce.png)
-
Coset representatives for
 in
in  are
are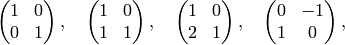
which we refer to below as
![[r_0], [r_1], [r_2],f](_images/math/4532d2bdeb09140fa285d546a813efa46b8de37e.png) and
and ![[r_3]](_images/math/0b50cc3385ecd0ce5c10366ec021fe88d9809aab.png) , respectively.
, respectively.In terms of representatives we have
![\begin{array}{ccc}
& [r_0]+[r_3]=0, & [r_0]+[r_3]+[r_2]=0, \\
& [r_1]+[r_2]=0, & [r_1]+[r_1]+[r_1]=0, \\
& [r_2]+[r_1]=0, & [r_2]+[r_0]+[r_3]=0, \\
& [r_3]+[r_0]=0, & [r_3]+[r_2]+[r_0]=0.
\end{array}](_images/math/5182c8382d8ea8ae308430009abe6e5d85d6d0dd.png)
By the first three relations we have
![[r_2] = [r_1] = 0 = 0[r_0]](_images/math/9a836e7d543388fd7586eba2503f56ce0a15f530.png) and
and ![[r_3] = -1[r_0]](_images/math/f3cfd37ce33850a3a7248938e946afd801074fdf.png) .
.Finally,
![\qquad\quad T_2([r_0]) & =
[r_0] \abcd{1}{0}{0}{2}
+ [r_0]\abcd{2 }{ 0 }{ 0 }{ 1}
+ [r_0]\abcd{2 }{ 1 }{ 0 }{ 1}
+ [r_0]\abcd{1 }{ 0 }{ 1 }{ 2} \\
& =
\left[ \abcd{1 }{ 0 }{ 0 }{ 2} \right]
+ \left[ \abcd{2 }{ 0 }{ 0 }{ 1} \right]
+ \left[ \abcd{2 }{ 1 }{ 0 }{ 1} \right]
+ \left[ \abcd{1 }{ 0 }{ 1 }{ 2} \right] \\
& = [r_0] + [r_0] + [r_0] + [r_2] \\
& = 3[r_0].](_images/math/0355db600cad120ea46af6cdba3560c1a74189fa.png)
Chapter 4¶
Exercise 4.1. Suppose
 is a Dirichlet character with modulus
is a Dirichlet character with modulus  .
Then
.
Then 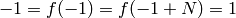 , a contradiction.
, a contradiction.-
Any finite subgroup of the multiplicative group of a field is cyclic (since the number of roots of a polynomial over a field is at most its degree), so
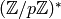 is cyclic. Let
is cyclic. Let  be an
integer that reduces to a generator of
be an
integer that reduces to a generator of 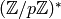 .
Let
.
Let 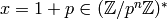 ; by the binomial theorem
; by the binomial theorem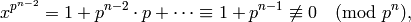
so
 has order
has order 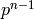 . Since
. Since  is odd,
is odd, 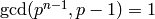 ,
so
,
so 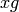 has order
has order 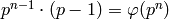 ; hence
; hence
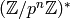 is cyclic.
is cyclic.By the binomial theorem
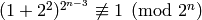 ,
so
,
so 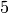 has order
has order 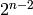 in
in 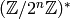 , and clearly
, and clearly 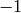 has
order
has
order  . Since
. Since 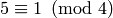 ,
, 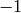 is not a power of
is not a power of 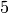 in
in
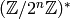 . Thus the subgroups
. Thus the subgroups 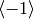 and
and 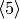 have trivial intersection.
The product of their orders is
have trivial intersection.
The product of their orders is 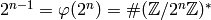 ,
so the claim follows.
,
so the claim follows.
Exercise 4.3. Write
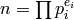 .
The order of
.
The order of  divides
divides  , so
the condition implies that
, so
the condition implies that 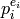 divides the order of
divides the order of  for each
for each  . Thus the order of
. Thus the order of  is divisible by the
least common multiple of the
is divisible by the
least common multiple of the 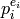 , i.e., by
, i.e., by  .
.-
The bijection given by
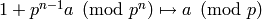 is a homomorphism since
is a homomorphism since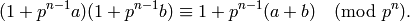
We have an exact sequence
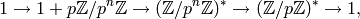
so it suffices to solve the discrete log problem in the kernel and cokernel. We prove by induction on
 that we can solve
the discrete log problem
in the kernel easily (compared to known methods for solving
the discrete log problem in
that we can solve
the discrete log problem
in the kernel easily (compared to known methods for solving
the discrete log problem in 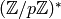 ).
We have an exact sequence
).
We have an exact sequence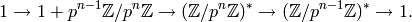
The first part of this problem shows that we can solve the discrete log problem in the kernel, and by induction we can solve it in the cokernel. This completes the proof.
Exercise 4.5. If
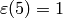 , then since
, then since  is
nontrivial, Exercise 4.2 implies
that
is
nontrivial, Exercise 4.2 implies
that  factors through
factors through 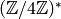 , hence has
conductor
, hence has
conductor 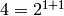 , as claimed.
If
, as claimed.
If 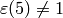 , then again from Exercise 4.2
we see that if
, then again from Exercise 4.2
we see that if  has order
has order  , then
, then  factors through
factors through 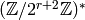 but nothing smaller.
but nothing smaller.-
- Take
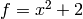 .
. - The element
 has order
has order 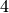 .
. - A minimal generator for
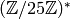 is
is  ,
and the characters are
,
and the characters are ![[1]](_images/math/97f62c4ffcbe7fb3f0086ce5307e5c37e663debe.png) ,
, ![[2]](_images/math/328fb8d24ad6bdb3accc0422d930ce2056246b2b.png) ,
, ![[3]](_images/math/e03715b6729d9f7ce309e3be666e535a0518d2a4.png) ,
, ![[4]](_images/math/0e96f6e7cec61c6139a5f822d04b935d4d3b3331.png) .
. - Each of the four Galois orbits has size
 .
.
- Take
Chapter 5¶
Exercise 5.1. The eigenspace
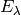 of
of  with eigenvalue
with eigenvalue 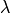 is
preserved by
is
preserved by  , since if
, since if 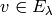 , then
, then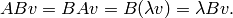
Because
 is diagonalizable, its minimal polynomial
equals its characteristic polynomial; hence the
same is true for the restriction of
is diagonalizable, its minimal polynomial
equals its characteristic polynomial; hence the
same is true for the restriction of  to
to 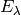 ,
i.e., the restriction of
,
i.e., the restriction of  is diagonalizable.
Choose basis for all
is diagonalizable.
Choose basis for all 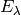 so that the
restrictions of
so that the
restrictions of  to these eigenspaces
is diagonal with respect to these bases. Then
the concatentation of these bases is a basis that
simultaneously diagonalizes
to these eigenspaces
is diagonal with respect to these bases. Then
the concatentation of these bases is a basis that
simultaneously diagonalizes  and
and  .
.Exercise 5.2. When
 is the trivial character, the
is the trivial character, the
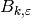 are defined by
are defined by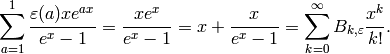
Thus
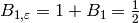 ,
and for
,
and for 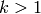 , we have
, we have 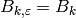 .
.Exercise 5.3. Omitted.
Exercise 5.4. The Eisenstein series in our basis for
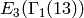 are of
the form
are of
the form 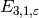 or
or 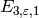 with
with 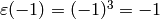 .
There are six characters
.
There are six characters  with modulus
with modulus 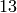 such that
such that 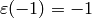 ,
and we have the two series
,
and we have the two series 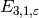 and
and
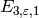 associated to each of these.
This gives a dimension of
associated to each of these.
This gives a dimension of 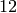 .
.
Chapter 6¶
-
By Proposition 3.10, we have
![[\SL_2(\Z):\Gamma_0(N)] = \#\P^1(\Z/N\Z)](_images/math/38f9b348cf307e00504bb40d10810e21bac31e83.png) .
By the Chinese Remainder Theorem,
.
By the Chinese Remainder Theorem,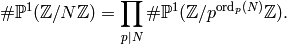
So we are reduced to computing
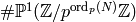 .
We have
.
We have 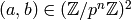 with
with 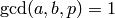 if and only if
if and only if 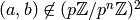 , so
there are
, so
there are 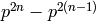 such pairs.
The unit group
such pairs.
The unit group 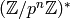 has order
has order 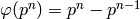 .
It follows that
.
It follows that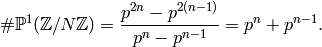
Omitted.
Exercise 6.2. Omitted.
Exercise 6.3. Omitted.
Exercise 6.4. Omitted.
Exercise 6.5. See the source code to Sage.
Chapter 7¶
Exercise 7.1. Take a basis of
 and let
and let  be the matrix
whose rows are these basis elements. Let
be the matrix
whose rows are these basis elements. Let
 be the row echelon form of
be the row echelon form of  .
After a permutation
.
After a permutation  of columns, we may
write
of columns, we may
write 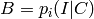 , where
, where 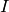 is the identity matrix.
The matrix
is the identity matrix.
The matrix 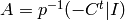 , where
, where 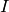 is a different
sized identity matrix, has the property that
is a different
sized identity matrix, has the property that
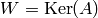 .
.Exercise 7.2. The answer is no. For example if
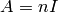 is
is  times the
identity matrix and if
times the
identity matrix and if 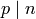 , then
, then 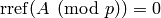 but
but 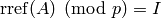 .
.Exercise 7.3. Let
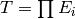 be an invertible matrix such that
be an invertible matrix such that 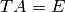 is
in (reduced) echelon form and the
is
in (reduced) echelon form and the 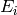 are elementary matrices,
i.e., the result of applying an elementary row operation to the
identity matrix. If
are elementary matrices,
i.e., the result of applying an elementary row operation to the
identity matrix. If  is a prime
that does not divide any of the nonzero numerators
or denominators of the entries of
is a prime
that does not divide any of the nonzero numerators
or denominators of the entries of  and any
and any 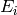 , then
, then
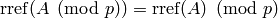 . This is
because
. This is
because 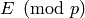 is in echelon form and
is in echelon form and 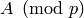 can be transformed to
can be transformed to 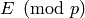 via a series of
elementary row operations modulo
via a series of
elementary row operations modulo  .
.-
The echelon form (over
 ) is
) is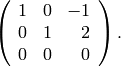
The kernel is the
 -dimensional span of
-dimensional span of
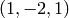 .
.The characteristic polynomial is
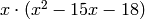 .
.
-
- The answer is given in the problem.
- See [Coh93, Section 2.4].
Chapter 8¶
Exercise 1.11. Using the Chinese Remainder Theorem we immediately reduce to proving the statement when both
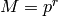 and
and 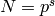 are powers
of a prime
are powers
of a prime  . Then
. Then ![[a]\in(\Z/p^s\Z)^*](_images/math/107d6755453a4185308b20077ef597be816dffa0.png) is represented by an
integer
is represented by an
integer  with
with 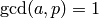 . That same integer
. That same integer  defines an element of
defines an element of 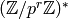 that reduces modulo
that reduces modulo
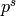 to
to ![[a]](_images/math/de38c39460667f504b7b57c3daa08d8d13cdaa9c.png) .
.Exercise 1.12. See [Shi94, Lemma 1.38].
Exercise 1.13. Coset representitives for
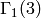 are in bijection with
are in bijection with 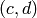 where
where
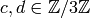 and
and 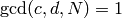 , so the following are representatives:
, so the following are representatives: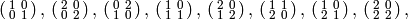
which we call
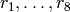 , respectively.
Now our Manin symbols are of the form
, respectively.
Now our Manin symbols are of the form ![[X,r_i]](_images/math/2714103546e7743dffd596216430cab285d711ca.png) and
and ![[Y, r_i]](_images/math/6affcb6a4ddcda631eacb8845bb9ed4ba9bfb865.png) for
for 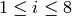 modulo the relations
modulo the relations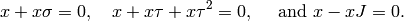
First, note that
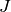 acts trivially on Manin symbols of odd weight because
it sends
acts trivially on Manin symbols of odd weight because
it sends 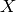 to
to 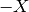 ,
, 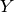 to
to 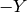 and
and 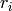 to
to 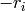 , so
, so![[z,g]J = [-z,-g] = [z,g].](_images/math/aa45e03fa85359c8b9d8a5ceec6daf8524a915aa.png)
Thus the last relation is trivially true.
Now
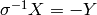 and
and 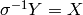 .
Also
.
Also 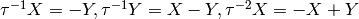 and
and 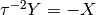 .
.The first relation on the first symbol says that
![[X, r_1] = -[-Y, r_3] = [Y, r_3]](_images/math/0aabb0c352698cf7761e8527c94d91a5976c7c0a.png)
and the second relation tells us that
![[X, r_1] + [-Y, r_5] + [-X+Y, r_6] = 0.](_images/math/b8211fabdeb1f4575d9a86efdc08350245c30060.png)
Exercise 1.14. Let
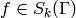 and
and 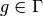 . All that remains to be
shown is that this pairing respects the relation
. All that remains to be
shown is that this pairing respects the relation 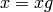 for all
modular symbols
for all
modular symbols  . By linearity it suffices to show the invariance of
. By linearity it suffices to show the invariance of
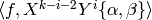 . We have
. We have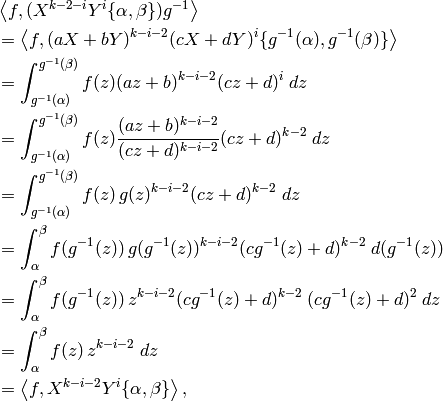
where the second to last simplification is due to invariance under
![[g]_k](_images/math/5e7b7d78728dca5fb387d935ed5f9de2eabb6c64.png) , i.e.,
, i.e.,![\qquad f(g^{-1}(z)) = f^{[g]_k}(g^{-1}(z)) = (cg^{-1}(z)+d)^{-k} f(g(g^{-1}(z))).](_images/math/d985f3794762fd250319ca1ccc8f9bc2681ef261.png)
- (The proof for
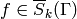 works in
works in exactly the same way.)
- (The proof for
-
Let
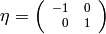 .
For any
.
For any 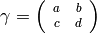 we have
we have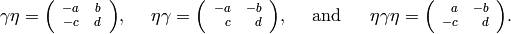
First, if
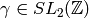 , then
, then 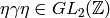 and
and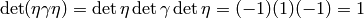
so
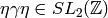 . As
. As 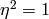 ,
conjugation by
,
conjugation by 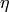 is self-inverse, so it must be a bijection.
is self-inverse, so it must be a bijection.Now if
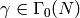 , then
, then 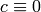 (mod
(mod  ), so
), so 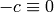 (mod
(mod  ), and so
), and so 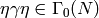 . Thus
. Thus
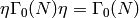 .
.If
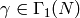 , then
, then 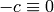 (mod
(mod  ) as before
and also
) as before
and also 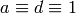 (mod
(mod  ), so
), so 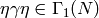 . Thus
. Thus 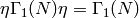 .
.Omitted.
Chapter 9¶
Exercise 9.1. Consider the surjective homomorphism
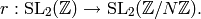
Notice that
 is the exact inverse image of the subgroup
is the exact inverse image of the subgroup 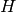 of
matrices of the form
of
matrices of the form 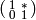 and
and  is the inverse image of the subroup
is the inverse image of the subroup  of upper triangular matrices.
It thus suffices to observe that
of upper triangular matrices.
It thus suffices to observe that 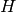 is normal in
is normal in  , which is clear.
Finally, the quotient
, which is clear.
Finally, the quotient 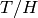 is isomorphic to the group of diagonal
matrices in
is isomorphic to the group of diagonal
matrices in 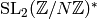 , which is isomorphic to
, which is isomorphic to  .
.Exercise 9.2. It is enough to show
![\dbd{p}\in\Z[\ldots,T_n,\ldots]](_images/math/758304c8ea4a4a83ef98923676ab4c2b5b7ece81.png) for
primes
for
primes  , since each
, since each 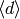 can be written in terms of the
can be written in terms of the
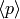 . Since
. Since 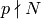 , we have that
, we have that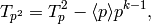
so
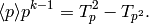
By Dirichlet’s theorem on primes in arithmetic progression, there is a prime
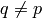 congruent
to
congruent
to  mod
mod  . Since
. Since 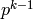 and
and 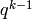 are relatively
prime, there exist integers
are relatively
prime, there exist integers  and
and 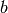 such that
such that 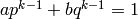 . Then
. Then![\qquad\dbd{p}=\dbd{p}(a p^{k-1} + b q^{k-1})
= a({T_p}^2-T_{p^2}) + b({T_q}^2-T_{q^2})
\in \Z[\ldots, T_n,\ldots].](_images/math/440cb6726be28d4332bfe2c4e4c1c622de008e18.png)
Exercise 9.3. Take
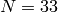 . The space
. The space 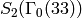 is a direct
sum of the two old subspaces coming from
is a direct
sum of the two old subspaces coming from 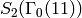 and the new subspace, which has dimension
and the new subspace, which has dimension  .
If
.
If  is a basis for
is a basis for 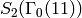 and
and
 is a basis for
is a basis for 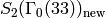 ,
then
,
then 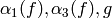 is a basis
for
is a basis
for 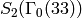 on which all Hecke
operators
on which all Hecke
operators  , with
, with 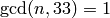 , have
diagonal matrix.
However, the operator
, have
diagonal matrix.
However, the operator
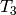 on
on 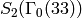 does
not act as a scalar on
does
not act as a scalar on 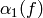 ,
so it cannot be in the ring generated
by all operators
,
so it cannot be in the ring generated
by all operators  with
with 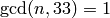 .
.Exercise 9.4. Omitted.
Chapter 10¶
-
Hint: Use either repeated integration by parts or a change of variables that relates the integral to the
 function.
function. Exercise 10.2. See [Cre97a, Section 2.8].
-
Let
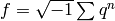 . Then
. Then 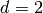 , but the nontrivial
conjugate of
, but the nontrivial
conjugate of  is
is 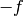 , so
, so 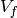 has dimension
has dimension  .
.Choose
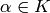 such that
such that 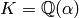 .
Write
.
Write(1)
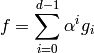
with
![g_i \in \Q[[q]]](_images/math/315de8dfaebaf8d4ac04d601dd7002d4caa066f5.png) .
Let
.
Let 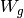 be the
be the  -span of the
-span of the  , and let
, and let
![W_f = V_f \cap \Q[[q]]](_images/math/33626e594c69783ddf2de05d72df4fb3a9f3dba4.png) .
By considering the
.
By considering the 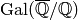 conjugates of (1),
we see that the Galois conjugates of
conjugates of (1),
we see that the Galois conjugates of  are in the
are in the  -span
of the
-span
of the  , so
, so(2)
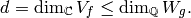
Likewise, taking the above modulo
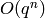 for any
for any  ,
we obtain a matrix equation
,
we obtain a matrix equation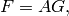
where the columns of
 are the
are the 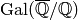 -conjugates of
-conjugates of
 , the matrix
, the matrix  is the Vandermonde matrix corresponding to
is the Vandermonde matrix corresponding to
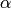 (and its
(and its 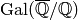 conjugates), and
conjugates), and  has
columns
has
columns  . Since
. Since  is a Vandermonde matrix, it is
invertible, so
is a Vandermonde matrix, it is
invertible, so 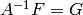 . Taking the limit as
. Taking the limit as  goes
to infinity, we see that each
goes
to infinity, we see that each  is a linear combination
of the
is a linear combination
of the 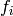 , hence an element of
, hence an element of 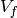 .
Thus
.
Thus 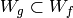 , so (2)
implies that
, so (2)
implies that 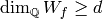 . But
. But 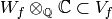 so finally
so finally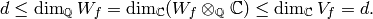
Exercise 10.4. See the appendix to Chapter II in [Cre97a], where this example is worked out in complete detail.