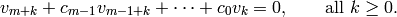Linear Algebra¶
This chapter is about several algorithms for matrix algebra over the rational numbers and cyclotomic fields. Algorithms for linear algebra over exact fields are necessary in order to implement the modular symbols algorithms that we will describe in Chapter Linear Algebra. This chapter partly overlaps with [Coh93, Sections 2.1–2.4].
Note: We view all matrices as defining linear transformations by acting on row vectors from the right.
Echelon Forms of Matrices¶
Definition 7.1
A matrix is in (reduced row) echelon form if each row in the matrix
has more zeros at the beginning than the row above it, the first
nonzero entry of every row is  , and the first nonzero entry of
any row is the only nonzero entry in its column.
, and the first nonzero entry of
any row is the only nonzero entry in its column.
Given a matrix  , there is another matrix
, there is another matrix  such that
such that  is
obtained from
is
obtained from  by left multiplication by an invertible matrix
and
by left multiplication by an invertible matrix
and  is in reduced row echelon form. This matrix
is in reduced row echelon form. This matrix  is called the
echelon form of
is called the
echelon form of  . It is unique.
. It is unique.
A pivot column of  is a column of
is a column of  such that the reduced
row echelon form of
such that the reduced
row echelon form of  contains a leading
contains a leading  .
.
Example 7.2
The following matrix is not in reduced row echelon form:
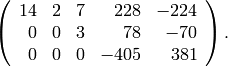
The reduced row echelon form of the above matrix is
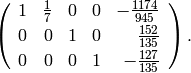
Notice that the entries of the reduced row echelon form can be
rationals with large denominators even though the entries of the
original matrix  are integers. Another example is the simple
looking matrix
are integers. Another example is the simple
looking matrix
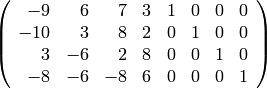
whose echelon form is

A basic fact is that two matrices  and
and  have the same reduced
row echelon form if and only if there is an invertible matrix
have the same reduced
row echelon form if and only if there is an invertible matrix  such
that
such
that 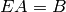 . Also, many standard operations in linear algebra,
e.g., computation of the kernel of a linear map, intersection of
subspaces, membership checking, etc., can be encoded as a question
about computing the echelon form of a matrix.
. Also, many standard operations in linear algebra,
e.g., computation of the kernel of a linear map, intersection of
subspaces, membership checking, etc., can be encoded as a question
about computing the echelon form of a matrix.
The following standard algorithm computes the echelon form of a matrix.
Algorithm 7.3
Given an 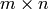 matrix
matrix  over a field,
the algorithm outputs the reduced row echelon form of
over a field,
the algorithm outputs the reduced row echelon form of  .
Write
.
Write 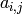 for the
for the 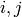 entry of
entry of  ,
where
,
where 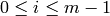 and
and 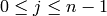 .
.
- [Initialize] Set
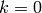 .
. - [Clear Each Column] For each column
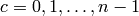 ,
clear the
,
clear the 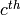 column as follows:
column as follows:- [First Nonzero] Find the smallest
 such that
such that
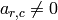 , or if there is no such
, or if there is no such  , go to the next
column.
, go to the next
column. - [Rescale] Replace row
 of
of  by
by 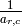 times row
times row  .
. - [Swap] Swap row
 with row
with row  .
. - [Clear] For each
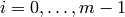 with
with 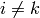 ,
if
,
if 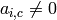 , add
, add 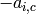 times row
times row  of
of  to
row
to
row  to clear the leading entry of the
to clear the leading entry of the 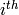 row.
row. - [Increment] Set
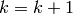 .
.
- [First Nonzero] Find the smallest
This algorithm takes 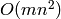 arithmetic operations in the base field,
where
arithmetic operations in the base field,
where  is an
is an 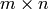 matrix. If the base field is
matrix. If the base field is  , the
entries can become huge and arithmetic operations are then
very expensive. See Section Echelon Forms over for ways
to mitigate this problem.
, the
entries can become huge and arithmetic operations are then
very expensive. See Section Echelon Forms over for ways
to mitigate this problem.
To conclude this section, we mention how to convert a few standard problems into questions about reduced row echelon forms of matrices. Note that one can also phrase some of these answers in terms of the echelon form, which might be easier to compute, or an LUP decomposition (lower triangular times upper triangular times permutation matrix), which the numerical analysts use.
Kernel of
 : We explain how to compute the
kernel of
: We explain how to compute the
kernel of  acting on column vectors from the right (first
transpose to obtain the kernel of
acting on column vectors from the right (first
transpose to obtain the kernel of  acting on row vectors).
Since passing to the reduced row echelon form of
acting on row vectors).
Since passing to the reduced row echelon form of  is the same
as multiplying on the left by an invertible matrix, the kernel of
the reduce row echelon form
is the same
as multiplying on the left by an invertible matrix, the kernel of
the reduce row echelon form  of
of  is the same as the kernel
of
is the same as the kernel
of  . There is a basis vector of
. There is a basis vector of 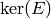 that corresponds to
each nonpivot column of
that corresponds to
each nonpivot column of  . That vector has a
. That vector has a  at the
nonpivot column,
at the
nonpivot column,  ‘s at all other nonpivot columns, and for each
pivot column, the negative of the entry of
‘s at all other nonpivot columns, and for each
pivot column, the negative of the entry of  at the nonpivot
column in the row with that pivot element.
at the nonpivot
column in the row with that pivot element.Intersection of Subspaces: Suppose
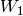 and
and 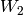 are subspace
of a finite-dimensional vector space
are subspace
of a finite-dimensional vector space  . Let
. Let 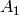 and
and 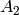 be
matrices whose columns form a basis for
be
matrices whose columns form a basis for 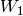 and
and 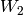 ,
respectively. Let
,
respectively. Let ![A=[A_1 | A_2]](_images/math/c04d9d985fe2b413bd3949ade54970579a165913.png) be the augmented matrix formed
from
be the augmented matrix formed
from 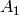 and
and 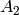 . Let
. Let 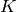 be the kernel of the linear
transformation defined by
be the kernel of the linear
transformation defined by  . Then
. Then 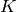 is isomorphic to the
desired intersection. To write down the intersection explicitly,
suppose that
is isomorphic to the
desired intersection. To write down the intersection explicitly,
suppose that 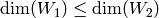 and do the following: For
each
and do the following: For
each 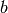 in a basis for
in a basis for 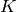 , write down the linear combination of a
basis for
, write down the linear combination of a
basis for 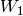 obtained by taking the first
obtained by taking the first 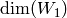 entries of
the vector
entries of
the vector 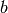 . The fact that
. The fact that 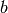 is in
is in 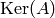 implies that the
vector we just wrote down is also in
implies that the
vector we just wrote down is also in 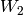 . This is because a
linear relation
. This is because a
linear relation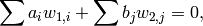
i.e., an element of that kernel, is the same as
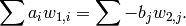
For more details, see [Coh93, Alg. 2.3.9].
Rational Reconstruction¶
Rational reconstruction is a process that allows one to sometimes lift
an integer modulo  uniquely to a bounded rational number.
uniquely to a bounded rational number.
Algorithm 7.4
Given an integer 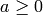 and an integer
and an integer 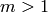 , this algorithm
computes the numerator
, this algorithm
computes the numerator  and denominator
and denominator  of the unique
rational number
of the unique
rational number 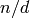 , if it exists, with
, if it exists, with
(1)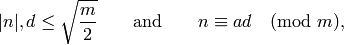
or it reports that there is no such number.
- [Reduce mod
 ] Replace
] Replace  with the least integer between
with the least integer between  and
and 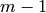 that is congruent to
that is congruent to  modulo
modulo  .
. - [Trivial Cases] If
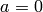 or
or 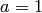 , return
, return  .
item{} [Initialize] Let
.
item{} [Initialize] Let 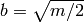 ,
, 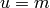 ,
,  , and set
, and set
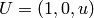 and
and 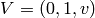 . Use the notation
. Use the notation 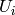 and
and 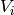 to refer to the
to refer to the 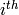 entries of
entries of 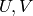 , for
, for 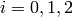 .
. - [Iterate] Do the following as long as
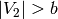 :
Set
:
Set 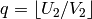 ,
set
,
set 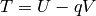 , and set
, and set 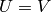 and
and 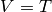 .
. - [Numerator and Denominator] Set
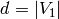 and
and 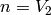 .
. - [Good?] If
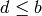 and
and 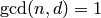 , return
, return 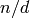 ;
otherwise report that there is no rational number as
in (1).
;
otherwise report that there is no rational number as
in (1).
Algorithm 7.4 for rational reconstruction is described (with proof) in [Knu, pgs. 656–657] as the solution to Exercise 51 on page 379 in that book. See, in particular, the paragraph right in the middle of page 657, which describes the algorithm. Knuth attributes this rational reconstruction algorithm to Wang, Kornerup, and Gregory from around 1983.
We now give an indication of why Algorithm 7.4 computes
the rational reconstruction of 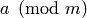 , leaving the precise
details and uniqueness to [Knu, pgs. 656–657]. At each
step in Algorithm 7.4, the
, leaving the precise
details and uniqueness to [Knu, pgs. 656–657]. At each
step in Algorithm 7.4, the  -tuple
-tuple 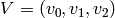 satisfies
satisfies
(2)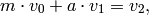
and similarly for 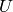 .
When computing the usual extended
.
When computing the usual extended 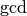 , at the end
, at the end 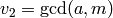 and
and 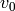 ,
, 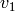 give a representation of the
give a representation of the 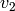 as a
as a 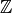 -linear
combination of
-linear
combination of  and
and  .
In Algorithm 7.4, we are instead interested
in finding a rational number
.
In Algorithm 7.4, we are instead interested
in finding a rational number 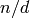 such that
such that
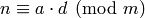 . If we set
. If we set 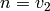 and
and 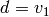 in (2) and rearrange, we obtain
in (2) and rearrange, we obtain
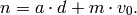
Thus at every step of the algorithm we find a rational number
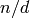 such that
such that 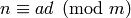 . The problem at intermediate
steps is that, e.g.,
. The problem at intermediate
steps is that, e.g., 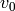 could be
could be  , or
, or  or
or  could be too large.
could be too large.
Example 7.5
We compute an example using Sage.
sage: p = 389
sage: k = GF(p)
sage: a = k(7/13); a
210
sage: a.rational_reconstruction()
7/13
Echelon Forms over  ¶
¶
A difficulty with computation of the echelon form of a matrix over the
rational numbers is that arithmetic with large rational numbers is
time-consuming; each addition potentially requires a 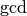 and numerous additions and multiplications of integers. Moreover, the
entries of
and numerous additions and multiplications of integers. Moreover, the
entries of  during intermediate steps of Algorithm 7.3
can be huge even though the entries of
during intermediate steps of Algorithm 7.3
can be huge even though the entries of  and the answer are small.
For example, suppose
and the answer are small.
For example, suppose  is an invertible square matrix. Then the
echelon form of
is an invertible square matrix. Then the
echelon form of  is the identity matrix, but during intermediate
steps the numbers involved could be quite large. One technique for
mitigating this is to compute the echelon form using a
multimodular method.
is the identity matrix, but during intermediate
steps the numbers involved could be quite large. One technique for
mitigating this is to compute the echelon form using a
multimodular method.
If  is a matrix with rational entries, let
is a matrix with rational entries, let 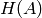 be the
height of
be the
height of  , which is the maximum of the absolute values of
the numerators and denominators of all entries of
, which is the maximum of the absolute values of
the numerators and denominators of all entries of  . If
. If 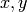 are
rational numbers and
are
rational numbers and  is a prime, we write
is a prime, we write 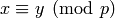 to
mean that the denominators of
to
mean that the denominators of  and
and 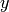 are not divisible by
are not divisible by  but
the numerator of the rational number
but
the numerator of the rational number 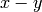 (in reduced form) is
divisible by
(in reduced form) is
divisible by  . For example, if
. For example, if 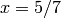 and
and 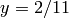 , then
, then
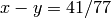 , so
, so 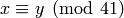 .
.
Algorithm 7.6
Given an 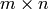 matrix
matrix  with entries in
with entries in  ,
this algorithm computes the reduced row echelon form of
,
this algorithm computes the reduced row echelon form of  .
.
Rescale the input matrix
 to have integer entries. This does
not change the echelon form and makes reduction modulo many
primes easier. We may thus assume
to have integer entries. This does
not change the echelon form and makes reduction modulo many
primes easier. We may thus assume  has integer entries.
has integer entries.Let
 be a guess for the height of the echelon form.
be a guess for the height of the echelon form.List successive primes
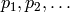 such that the product
of the
such that the product
of the 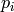 is greater than
is greater than 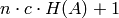 , where
, where
 is the number of columns of
is the number of columns of  .
.Compute the echelon forms
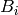 of the reduction
of the reduction 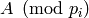 using, e.g., Algorithm 7.3 or any other echelon algorithm. %
(This is where most of the work takes place.)
using, e.g., Algorithm 7.3 or any other echelon algorithm. %
(This is where most of the work takes place.)Discard any
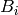 whose pivot column list is not maximal among
pivot lists of all
whose pivot column list is not maximal among
pivot lists of all 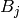 found so far. (The pivot list
associated to
found so far. (The pivot list
associated to 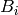 is the ordered list of integers
is the ordered list of integers  such
that the
such
that the 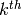 column of
column of 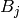 is a pivot column. We mean
maximal with respect to the following ordering on integer
sequences: shorter integer sequences are smaller, and if two
sequences have the same length, then order in reverse
lexicographic order. Thus
is a pivot column. We mean
maximal with respect to the following ordering on integer
sequences: shorter integer sequences are smaller, and if two
sequences have the same length, then order in reverse
lexicographic order. Thus ![[1,2]](_images/math/92bb4c21c8491453be13b7f2d521b1934160031f.png) is smaller than
is smaller than ![[1,2,3]](_images/math/e8dd506f76559bbb9c2095066d6957f810c5e6f4.png) ,
and
,
and ![[1,2,7]](_images/math/c8420c4644c18a2ba96be4cb91c09dafb337dfab.png) is smaller than
is smaller than ![[1,2,5]](_images/math/70945f442c2f9afa027c81f961e7889091d24286.png) . Think of maximal as
“optimal”, i.e., best possible pivot columns.)
. Think of maximal as
“optimal”, i.e., best possible pivot columns.)Use the Chinese Remainder Theorem to find a matrix
 with
integer entries such that
with
integer entries such that 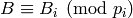 for all
for all 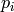 .
.Use Algorithm 7.4 to try to find a matrix
 whose
coefficients are rational numbers
whose
coefficients are rational numbers 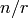 such that
such that
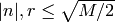 , where
, where 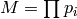 , and
, and 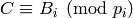 for each prime
for each prime  . If rational reconstruction fails, compute a
few more echelon forms mod the next few primes (using the above
steps) and attempt rational reconstruction again. Let
. If rational reconstruction fails, compute a
few more echelon forms mod the next few primes (using the above
steps) and attempt rational reconstruction again. Let  be
the matrix over
be
the matrix over  so obtained. (A trick here is to keep
track of denominators found so far to avoid doing very many
rational reconstructions.)
so obtained. (A trick here is to keep
track of denominators found so far to avoid doing very many
rational reconstructions.)Compute the denominator
 of
of  , i.e., the smallest positive
integer such that
, i.e., the smallest positive
integer such that 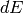 has integer entries. If
has integer entries. If(3)
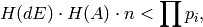
then
 is the reduced row echelon form of
is the reduced row echelon form of  . If not,
repeat the above steps with a few more primes.
. If not,
repeat the above steps with a few more primes.
Proof
We prove that if (3) is satisfied, then the
matrix  computed by the algorithm really is the reduced row
echelon form
computed by the algorithm really is the reduced row
echelon form  of
of  . First note that
. First note that  is in reduced row
echelon form since the set of pivot columns of all matrices
is in reduced row
echelon form since the set of pivot columns of all matrices 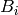 used to construct
used to construct  are the same, so the pivot columns of
are the same, so the pivot columns of  are
the same as those of any
are
the same as those of any 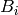 and all other entries in the
and all other entries in the 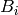 pivot columns are
pivot columns are  , so the other entries of
, so the other entries of  in the pivot
columns are also
in the pivot
columns are also  .
.
Recall from the end of Section Echelon Forms of Matrices that a matrix
whose columns are a basis for the kernel of  can be obtained from
the reduced row echelon form
can be obtained from
the reduced row echelon form  . Let
. Let 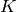 be the matrix whose
columns are the vectors in the kernel algorithm applied to
be the matrix whose
columns are the vectors in the kernel algorithm applied to  ,
so
,
so 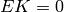 . Since the reduced row echelon form is obtained by left
multiplying by an invertible matrix, for each
. Since the reduced row echelon form is obtained by left
multiplying by an invertible matrix, for each  , there is
an invertible matrix
, there is
an invertible matrix 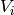 mod
mod 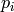 such that
such that 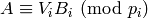 so
so
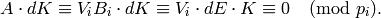
Since 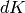 and
and  are integer matrices, the Chinese
remainder theorem implies that
are integer matrices, the Chinese
remainder theorem implies that
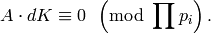
The integer entries  of
of 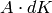 all satisfy
all satisfy
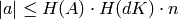 ,
where
,
where  is the number of columns of
is the number of columns of  . Since
. Since 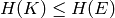 ,
the bound (3) implies that
,
the bound (3) implies that 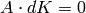 . Thus
. Thus
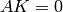 , so
, so 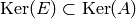 . On the other hand,
the rank of
. On the other hand,
the rank of  equals the rank of each
equals the rank of each 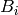 (since the pivot columns
are the same), so
(since the pivot columns
are the same), so
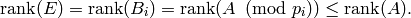
Thus 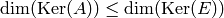 , and combining
this with the bound obtained above, we see that
, and combining
this with the bound obtained above, we see that
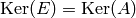 . This implies that
. This implies that  is the reduced row
echelon form of
is the reduced row
echelon form of  , since two matrices have the same kernel if
and only if they have the same reduced row echelon form
(the echelon form is an invariant of the row space, and the
kernel is the orthogonal complement of the row space).
, since two matrices have the same kernel if
and only if they have the same reduced row echelon form
(the echelon form is an invariant of the row space, and the
kernel is the orthogonal complement of the row space).
The reason for step (5) is that the matrices 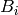 need
not be the reduction of
need
not be the reduction of  modulo
modulo 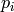 , and indeed this
reduction might not even be defined, e.g., if
, and indeed this
reduction might not even be defined, e.g., if 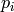 divides the
denominator of some element of
divides the
denominator of some element of  , then this reduction makes no
sense. For example, set
, then this reduction makes no
sense. For example, set 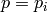 and suppose
and suppose 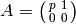 .
Then
.
Then 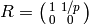 , which has no reduction modulo
, which has no reduction modulo  ; also,
the reduction of
; also,
the reduction of  modulo
modulo 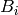 is
is 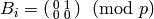 , which is already in reduced row echelon form. However if
we were to combine
, which is already in reduced row echelon form. However if
we were to combine 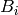 with the echelon form of
with the echelon form of  modulo another
prime, the result could never be lifted using rational reconstruction.
Thus the reason we exclude all
modulo another
prime, the result could never be lifted using rational reconstruction.
Thus the reason we exclude all 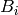 with nonmaximal pivot column
sequence is so that a rational reconstruction will exist. There are
only finitely many primes that divide denominators of entries of
with nonmaximal pivot column
sequence is so that a rational reconstruction will exist. There are
only finitely many primes that divide denominators of entries of  ,
so eventually all
,
so eventually all 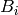 will have maximal pivot column sequences,
i.e., they are the reduction of the true reduced row echelon form
will have maximal pivot column sequences,
i.e., they are the reduction of the true reduced row echelon form  , so
the algorithm terminates.
, so
the algorithm terminates.
Remark 7.7
Algorithm 7.6, with sparse matrices seems to
work very well in practice. A simple but helpful
modification to Algorithm 7.3 in the sparse case is to
clear each column using a row with a minimal number of nonzero
entries, so as to reduce the amount of “fill in” (denseness) of
the matrix. There are much more sophisticated methods along these
lines called “intelligent Gauss elimination”. (Cryptographers are
interested in linear algebra mod  with huge sparse matrices,
since they come up in attacks on the discrete log problem and
integer factorization.)
with huge sparse matrices,
since they come up in attacks on the discrete log problem and
integer factorization.)
One can adapt Algorithm 7.6 to computation of
echelon forms of matrices  over cyclotomic fields
over cyclotomic fields 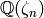 .
Assume
.
Assume  has denominator
has denominator  . Let
. Let  be a prime that splits
completely in
be a prime that splits
completely in 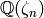 . Compute the homomorphisms
. Compute the homomorphisms
![f_i : \Z_p[\zeta_n] \to \F_p](_images/math/2e4bbd1e593ad956016d56e9d131ff5a24adf7d5.png) by finding the elements of order
by finding the elements of order  in
in
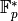 . Then compute the mod
. Then compute the mod  matrix
matrix 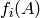 for each
for each  , and
find its reduced row echelon form. Taken together, the maps
, and
find its reduced row echelon form. Taken together, the maps 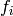 together induce an isomorphism
together induce an isomorphism ![\Psi:\F_p[X]/\Phi_n(X) \isom \F_p^d](_images/math/8450552c7c3c087b1c6b732ff780a52af265832d.png) ,
where
,
where 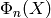 is the
is the 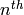 cyclotomic polynomial and
cyclotomic polynomial and  is its
degree. It is easy to compute
is its
degree. It is easy to compute 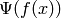 by evaluating
by evaluating 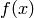 at
each element of order
at
each element of order  in
in 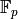 . To compute
. To compute 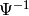 , simply
use linear algebra over
, simply
use linear algebra over 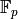 to invert a matrix that represents
to invert a matrix that represents
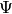 . Use
. Use 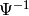 to compute the reduced row echelon form of
to compute the reduced row echelon form of
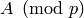 , where
, where 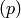 is the nonprime ideal in
is the nonprime ideal in ![\Z[\zeta_n]](_images/math/a51ab57040f45871738bba73241297da2d3f3ce7.png) generated by
generated by  . Do this for several primes
. Do this for several primes  , and use rational
reconstruction on each coefficient of each power of
, and use rational
reconstruction on each coefficient of each power of 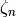 , to
recover the echelon form of
, to
recover the echelon form of  .
.
Echelon Forms via Matrix Multiplication¶
In this section we explain
how to compute echelon forms using matrix multiplication. This is
valuable because there are asymptotically fast, i.e., better than
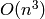 field operations, algorithms for matrix multiplication, and
implementations of linear algebra libraries often include
highly optimized matrix multiplication algorithms.
We only sketch the basic ideas
behind these asymptotically fast algorithms (following [Ste]), since more
detail would take us too far from modular forms.
field operations, algorithms for matrix multiplication, and
implementations of linear algebra libraries often include
highly optimized matrix multiplication algorithms.
We only sketch the basic ideas
behind these asymptotically fast algorithms (following [Ste]), since more
detail would take us too far from modular forms.
The naive algorithm for multiplying two 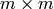 matrices requires
matrices requires
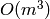 arithmetic operations in the base ring. In
[Str69], Strassen described a clever algorithm that
computes the product of two
arithmetic operations in the base ring. In
[Str69], Strassen described a clever algorithm that
computes the product of two 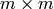 matrices in
matrices in 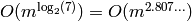 arithmetic operations in the base ring. Because
of numerical stability issues, Strassen’s algorithm is rarely used in
numerical analysis. But for matrix arithmetic over exact base rings
(e.g., the rational numbers, finite fields, etc.) it is of extreme
importance.
arithmetic operations in the base ring. Because
of numerical stability issues, Strassen’s algorithm is rarely used in
numerical analysis. But for matrix arithmetic over exact base rings
(e.g., the rational numbers, finite fields, etc.) it is of extreme
importance.
In [Str69], Strassen also sketched a new algorithm for
computing the inverse of a square matrix using matrix multiplication.
Using this algorithm, the number of operations to invert an 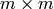 matrix is (roughly) the same as the number needed to multiply two
matrix is (roughly) the same as the number needed to multiply two
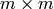 matrices.
Suppose the input matrix is
matrices.
Suppose the input matrix is 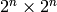 and we
write it in block form as
and we
write it in block form as 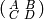 where
where 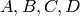 are all
are all
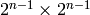 matrices. Assume that any intermediate
matrices below that we invert are invertible. Consider the augmented
matrix
matrices. Assume that any intermediate
matrices below that we invert are invertible. Consider the augmented
matrix
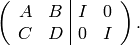
Multiply the top row by 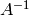 to obtain
to obtain
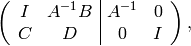
and write 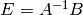 .
Subtract
.
Subtract  times the first row from the second row to get
times the first row from the second row to get
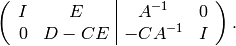
Set 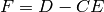 and multiply
the bottom row by
and multiply
the bottom row by 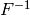 on the left to obtain
on the left to obtain
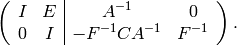
Set 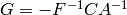 , and subtract
, and subtract  times the second from the first row to
arrive at
times the second from the first row to
arrive at
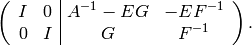
The idea listed above can, with significant work, be extended to a general algorithm (as is done in [Ste06]).
Next we very briefly sketch how to compute echelon forms of matrices using matrix multiplication and inversion. Its complexity is comparable to the complexity of matrix multiplication.
As motivation, recall the standard algorithm from undergraduate linear
algebra for inverting an invertible square matrix  : form the
augmented matrix
: form the
augmented matrix ![[A|I]](_images/math/1e8da60a7579a29f7560860be44b69ffb45a3d7d.png) , and then compute the echelon form of this
matrix, which is
, and then compute the echelon form of this
matrix, which is ![[I|A^{-1}]](_images/math/6ce82166c1225c94c1c2499e57399dc59b7cd2c5.png) . If
. If  is the transformation matrix to
echelon form, then
is the transformation matrix to
echelon form, then ![T[A|I] = [I|T]](_images/math/231a23c28054f49699b81ce7aff1be46d23e0596.png) , so
, so 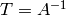 . In particular, we
could find the echelon form of
. In particular, we
could find the echelon form of ![[A|I]](_images/math/1e8da60a7579a29f7560860be44b69ffb45a3d7d.png) by multiplying on the left by
by multiplying on the left by
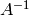 . Likewise, for any matrix
. Likewise, for any matrix  with the same number of rows
as
with the same number of rows
as  , we could find the echelon form of
, we could find the echelon form of ![[A|B]](_images/math/bf14e657075e8443b1bccb621f1526785ddb27ae.png) by multiplying on
the left by
by multiplying on
the left by 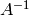 . Next we extend this idea to give
an algorithm to compute echelon forms using only matrix multiplication (and
echelon form modulo one prime).
. Next we extend this idea to give
an algorithm to compute echelon forms using only matrix multiplication (and
echelon form modulo one prime).
Algorithm 7.8
Given a matrix  over the rational numbers (or a number field),
this algorithm computes the echelon form of
over the rational numbers (or a number field),
this algorithm computes the echelon form of  .
.
1. [Find Pivots] Choose a random prime  (coprime to the
denominator of any entry of
(coprime to the
denominator of any entry of  ) and compute the echelon form of
) and compute the echelon form of
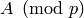 , e.g., using Algorithm 7.3. Let
, e.g., using Algorithm 7.3. Let 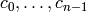 be the pivot columns of
be the pivot columns of 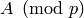 . When computing the
echelon form, save the positions
. When computing the
echelon form, save the positions 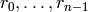 of the rows
used to clear each column.
of the rows
used to clear each column.
- [Extract Submatrix] Extract the
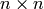 submatrix
submatrix  of
of  whose entries are
whose entries are 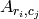 for
for 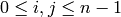 .
. - [Compute Inverse] Compute the inverse
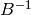 of
of  . Note
that
. Note
that  must be invertible since its reduction modulo
must be invertible since its reduction modulo  is
invertible.
is
invertible. - [Multiply] Let
 be the matrix whose rows are the rows
be the matrix whose rows are the rows
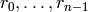 of
of  . Compute
. Compute 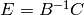 . If
. If  is
not in echelon form, go to ste (1).
is
not in echelon form, go to ste (1). - [Done?] Write down a matrix
 whose columns are a basis for
whose columns are a basis for
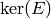 as explained in the Kernel Algorithm. Let
as explained in the Kernel Algorithm. Let  be
the matrix whose rows are the rows of
be
the matrix whose rows are the rows of  other than rows
other than rows
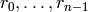 . Compute the product
. Compute the product 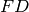 . If
. If 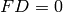 ,
output
,
output  , which is the echelon form of
, which is the echelon form of  . If
. If 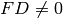 , go
to step (1)) and run the whole algorithm
again.
, go
to step (1)) and run the whole algorithm
again.
Proof
We prove both that the algorithm terminates and that when it
terminates, the matrix  is the echelon form of
is the echelon form of  .
.
First we prove that the algorithm terminates. Let  be the
echelon form of
be the
echelon form of  .
By Exercise 7.3,
for all but finitely many primes
.
By Exercise 7.3,
for all but finitely many primes  (i.e., any
prime where
(i.e., any
prime where 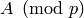 has the same rank as
has the same rank as  ) the echelon form of
) the echelon form of
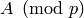 equals
equals 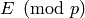 . For any such prime
. For any such prime  the pivot
columns of
the pivot
columns of 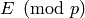 are the pivot columns of
are the pivot columns of  , so the
algorithm will terminate for that choice of
, so the
algorithm will terminate for that choice of  .
.
We next prove that when the algorithm terminates,  is the
echelon form of
is the
echelon form of  . By assumption,
. By assumption,  is in echelon form and is
obtained by multiplying
is in echelon form and is
obtained by multiplying  on the left by an invertible matrix,
so
on the left by an invertible matrix,
so  must be the echelon form of
must be the echelon form of  . The rows of
. The rows of  are a
subset of those of
are a
subset of those of  , so the rows of
, so the rows of  are a subset of the rows
of the echelon form of
are a subset of the rows
of the echelon form of  . Thus
. Thus 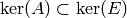 . To
show that
. To
show that  equals the echelon form of
equals the echelon form of  , we just need to verify
that
, we just need to verify
that 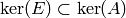 , i.e., that
, i.e., that 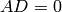 , where
, where  is as in
step (5). Since
is as in
step (5). Since  is the echelon form of
is the echelon form of  , we
know that
, we
know that 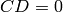 . By step (5) we also know that
. By step (5) we also know that
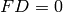 . Thus
. Thus 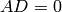 , since the rows of
, since the rows of  are the union of the
rows of
are the union of the
rows of  and
and  .
.
Example 7.9
Let  be the
be the 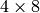 matrix
matrix
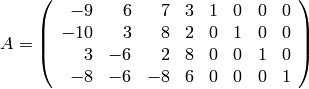
from Example 7.2.
sage: M = MatrixSpace(QQ,4,8)
sage: A = M([[-9,6,7,3,1,0,0,0],[-10,3,8,2,0,1,0,0],
[3,-6,2,8,0,0,1,0],[-8,-6,-8,6,0,0,0,1]])
First choose the “random” prime 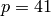 , which does not
divide any of the entries of
, which does not
divide any of the entries of  , and compute the
echelon form of the reduction of
, and compute the
echelon form of the reduction of  modulo
modulo 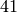 .
.
sage: A41 = MatrixSpace(GF(41),4,8)(A)
sage: E41 = A41.echelon_form()
The echelon form of 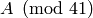 is
is
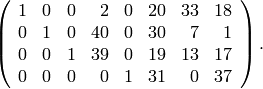
Thus we take  ,
,  ,
, 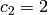 , and
, and 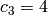 .
Also
.
Also 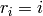 for
for 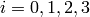 .
Next extract the submatrix
.
Next extract the submatrix  .
.
sage: B = A.matrix_from_columns([0,1,2,4])
The submatrix  is
is
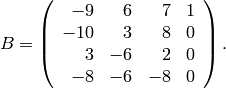
The inverse of  is
is

Multiplying by  yields
yields
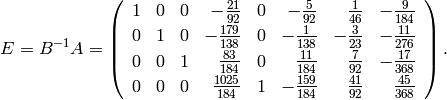
sage: E = B^(-1)*A
This is not the echelon form of  . Indeed, it is not
even in echelon form, since the last row is not
normalized so the leftmost nonzero entry is
. Indeed, it is not
even in echelon form, since the last row is not
normalized so the leftmost nonzero entry is  .
We thus choose another random prime, say
.
We thus choose another random prime, say 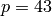 .
The echelon form mod
.
The echelon form mod 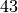 has columns
has columns 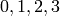 as pivot columns.
We thus extract the matrix
as pivot columns.
We thus extract the matrix
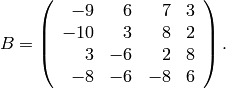
sage: B = A.matrix_from_columns([0,1,2,3])
This matrix has inverse
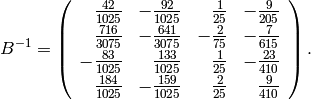
Finally, the echelon form of  is
is 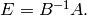 No further
checking is needed since the product so obtained is in echelon
form, and the matrix
No further
checking is needed since the product so obtained is in echelon
form, and the matrix  of the last step of the algorithm has
of the last step of the algorithm has  rows.
rows.
Remark 7.10
Above we have given only the barest sketch of asymptotically fast “block” algorithms for linear algebra. For optimized algorithms that work in the general case, please see the source code of [Ste06].
Decomposing Spaces under the Action of Matrix¶
Efficiently solving the following problem is a crucial step in computing a basis of eigenforms for a space of modular forms (see Sections Computing Using Eigenvectors and Newforms: Systems of Eigenvalues).
Problem 7.11
Suppose  is an
is an 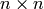 matrix with entries in a field
matrix with entries in a field 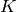 (typically a number field or finite field) and that the minimal
polynomial of
(typically a number field or finite field) and that the minimal
polynomial of  is square-free and has degree
is square-free and has degree  . View
. View  as
acting on
as
acting on 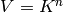 . Find a simple module decomposition
. Find a simple module decomposition 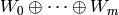 of
of  as a direct sum of simple
as a direct sum of simple ![K[T]](_images/math/7619d30d16974a3af86a1e8c76839bbba3370b99.png) -modules.
Equivalently, find an invertible matrix
-modules.
Equivalently, find an invertible matrix  such that
such that 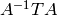 is a block direct sum of matrices
is a block direct sum of matrices 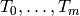 such that the
minimal polynomial of each
such that the
minimal polynomial of each 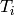 is irreducible.
is irreducible.
Remark 7.12
A generalization of Problem 7.11
to arbitrary matrices with entries in  is
finding the rational Jordan form (or rational canonical
form, or Frobenius form) of
is
finding the rational Jordan form (or rational canonical
form, or Frobenius form) of  .
This is like the usual Jordan form, but the resulting matrix is
over
.
This is like the usual Jordan form, but the resulting matrix is
over  and the summands of the matrix corresponding to
eigenvalues are replaced by matrices whose minimal polynomials
are the minimal polynomials (over
and the summands of the matrix corresponding to
eigenvalues are replaced by matrices whose minimal polynomials
are the minimal polynomials (over  ) of the eigenvalues. The
rational Jordan form was extensively studied by Giesbrecht in his
Ph.D. thesis and many successive papers, where he analyzes the
complexity of his algorithms and observes that the limiting step is
factoring polynomials over
) of the eigenvalues. The
rational Jordan form was extensively studied by Giesbrecht in his
Ph.D. thesis and many successive papers, where he analyzes the
complexity of his algorithms and observes that the limiting step is
factoring polynomials over 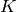 . The reason is that given a polynomial
. The reason is that given a polynomial
![f\in K[x]](_images/math/039f104206d80a9cd87a7e60701edff251773932.png) , one can easily write down a matrix
, one can easily write down a matrix  such that one can
read off the factorization of
such that one can
read off the factorization of  from the rational Jordan form of
from the rational Jordan form of
 (see also [Ste97]).
(see also [Ste97]).
Characteristic Polynomials¶
The computation of characteristic polynomials of matrices is crucial to
modular forms computations. There are many approaches to this
problems: compute 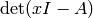 symbolically (bad), compute the traces
of the powers of
symbolically (bad), compute the traces
of the powers of  (bad), or compute the Hessenberg form modulo many
primes and use CRT (bad; see for [Coh93, Section 2.2.4] the
definition of Hessenberg form and the algorithm). A more
sophisticated method is to compute the rational canonical form of
(bad), or compute the Hessenberg form modulo many
primes and use CRT (bad; see for [Coh93, Section 2.2.4] the
definition of Hessenberg form and the algorithm). A more
sophisticated method is to compute the rational canonical form of  using Giesbrecht’s algorithm [1] (see [GS02]),
which involves computing Krylov subspaces
(see Remark Remark 7.13 below), and building up the whole
space on which
using Giesbrecht’s algorithm [1] (see [GS02]),
which involves computing Krylov subspaces
(see Remark Remark 7.13 below), and building up the whole
space on which  acts. This latter method is a generalization of
Wiedemann’s algorithm for computing minimal polynomials (see
Section Wiedemann’s Minimal Polynomial Algorithm), but with more structure to handle the
case when the characteristic polynomial is not equal to the minimal
polynomial.
acts. This latter method is a generalization of
Wiedemann’s algorithm for computing minimal polynomials (see
Section Wiedemann’s Minimal Polynomial Algorithm), but with more structure to handle the
case when the characteristic polynomial is not equal to the minimal
polynomial.
Polynomial Factorization¶
Factorization of polynomials in ![\Q[X]](_images/math/175755dc07dfb52becffdc117a4590a8d3970ac4.png) (or over number fields) is an
important step in computing an explicit basis of Hecke eigenforms for
spaces of modular forms. The best algorithm is the van Hoeij method
[BHKS06],
which uses the LLL lattice basis reduction algorithm [LLL82] in a
novel way to solve the optimization problems that come up in trying to
lift factorizations mod
(or over number fields) is an
important step in computing an explicit basis of Hecke eigenforms for
spaces of modular forms. The best algorithm is the van Hoeij method
[BHKS06],
which uses the LLL lattice basis reduction algorithm [LLL82] in a
novel way to solve the optimization problems that come up in trying to
lift factorizations mod  to
to 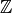 .
It has been generalized by Belebas, van Hoeij, Kl”uners, and Steel
to number fields.
.
It has been generalized by Belebas, van Hoeij, Kl”uners, and Steel
to number fields.
Wiedemann’s Minimal Polynomial Algorithm¶
In this section we describe
an algorithm due to Wiedemann for computing the
minimal polynomial of an 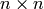 matrix
matrix  over a field.
over a field.
Choose a random vector  and compute the iterates
and compute the iterates
(4)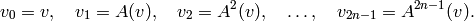
If 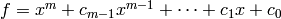 is the minimal polynomial of
is the minimal polynomial of  , then
, then
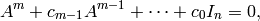
where 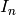 is the
is the 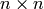 identity matrix.
For any
identity matrix.
For any 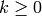 , by
multiplying both sides on the right by the vector
, by
multiplying both sides on the right by the vector 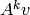 , we see that
, we see that
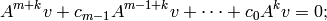
hence
Wiedemann’s idea is to observe that any single component of the
vectors 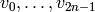 satisfies the linear recurrence with
coefficients
satisfies the linear recurrence with
coefficients 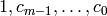 . The Berlekamp-Massey
algorithm (see Algorithm 7.14 below) was introduced in the
1960s in the context of coding theory to find the minimal polynomial
of a linear recurrence sequence
. The Berlekamp-Massey
algorithm (see Algorithm 7.14 below) was introduced in the
1960s in the context of coding theory to find the minimal polynomial
of a linear recurrence sequence 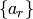 . The minimal polynomial of
this linear recurrence is by definition the unique monic
polynomial
. The minimal polynomial of
this linear recurrence is by definition the unique monic
polynomial  , such that if
, such that if 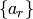 satisfies a linear recurrence
satisfies a linear recurrence
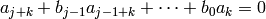 (for all
(for all 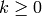 ), then
), then  divides the polynomial
divides the polynomial 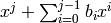 .
If we apply Berlekamp-Massey to the top coordinates of the
.
If we apply Berlekamp-Massey to the top coordinates of the 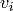 , we
obtain a polynomial
, we
obtain a polynomial 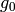 , which divides
, which divides  . We then apply it to the
second to the top coordinates and find a polynomial
. We then apply it to the
second to the top coordinates and find a polynomial 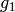 that
divides
that
divides  , etc. Taking the least common multiple of the first few
, etc. Taking the least common multiple of the first few  , we
find a divisor of the minimal polynomial of
, we
find a divisor of the minimal polynomial of  . One can show that
with “high probability” one quickly finds
. One can show that
with “high probability” one quickly finds  , instead of just a
proper divisor of
, instead of just a
proper divisor of  .
.
Remark 7.13
In the literature, techniques that involve iterating a vector as in (4) are often called Krylov methods. The subspace generated by the iterates of a vector under a matrix is called a Krylov subspace.
Algorithm 7.14
Suppose 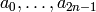 are the first
are the first 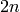 terms of a
sequence that satisfies a linear recurrence of degree at most
terms of a
sequence that satisfies a linear recurrence of degree at most  .
This algorithm computes the minimal
polynomial
.
This algorithm computes the minimal
polynomial  of the sequence.
of the sequence.
- Let
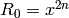 ,
, 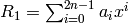 ,
,
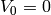 ,
, 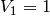 .
. - While
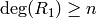 , do the following:
, do the following:- Compute
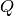 and
and  such that
such that 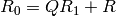 .
. - Let
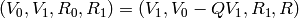 .
.
- Compute
- Let
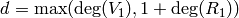 and set
and set
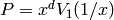 .
. - Let
 be the leading coefficient of
be the leading coefficient of 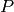 and output
and output
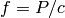 .
.
The above description of Berlekamp-Massey is taken from [AD04], which contains some additional ideas for improvements.
Now suppose  is an
is an 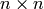 matrix as in
Problem Problem 7.11. We find the minimal polynomial of
matrix as in
Problem Problem 7.11. We find the minimal polynomial of  by
computing the minimal polynomial of
by
computing the minimal polynomial of 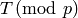 using Wiedemann’s
algorithm, for many primes
using Wiedemann’s
algorithm, for many primes  , and using the Chinese Remainder
Theorem. (One has to bound the number of primes that must be
considered; see, e.g., [Coh93].)
, and using the Chinese Remainder
Theorem. (One has to bound the number of primes that must be
considered; see, e.g., [Coh93].)
One can also compute the characteristic polynomial of  directly
from the Hessenberg form of
directly
from the Hessenberg form of  , which can be computed in
, which can be computed in 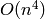 field operations, as described in [Coh93]. This is
simple but slow. Also, the
field operations, as described in [Coh93]. This is
simple but slow. Also, the  we consider will often be sparse,
and Wiedemann is particularly good when
we consider will often be sparse,
and Wiedemann is particularly good when  is sparse.
is sparse.
Example 7.15
We compute the minimal polynomial of
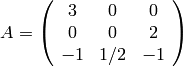
using Wiedemann’s algorithm. Let 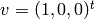 . Then
. Then
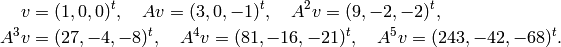
The linear recurrence sequence coming from the first entries is
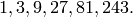
This sequence satisfies the linear recurrence
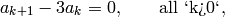
so its minimal polynomial is 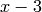 . This implies that
. This implies that
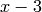 divides the minimal polynomial of the matrix
divides the minimal polynomial of the matrix  .
Next we use the sequence of second coordinates of the
iterates of
.
Next we use the sequence of second coordinates of the
iterates of  , which is
, which is
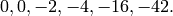
The recurrence that this sequence satisfies is slightly
less obvious, so we apply the Berlekamp-Massey algorithm
to find it, with 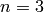 .
.
We have
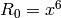 ,
, 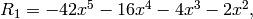
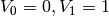 .
.Dividing
 by
by  , we find
, we find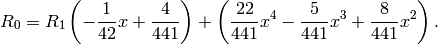
The new
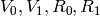 are
are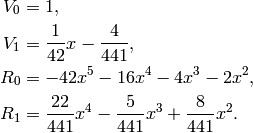
Since
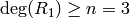 , we do the above three steps again.
, we do the above three steps again.
We repeat the above three steps.
Dividing
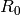 by
by 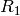 , we find
, we find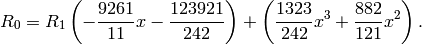
The new
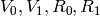 are:
are: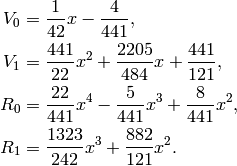
We have to repeat the steps yet again:
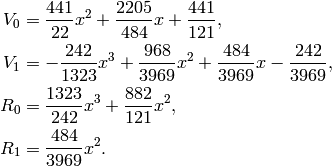
We have
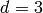 ,
so
,
so 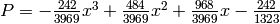 .
.Multiply through by
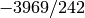 and output
and output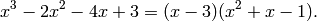
The minimal polynomial of  is
is 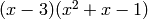 ,
since the minimal polynomial has degree at most
,
since the minimal polynomial has degree at most  and is divisible by
and is divisible by 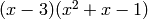 .
.
 -adic Nullspace¶
-adic Nullspace¶
We will use the following algorithm of Dixon [Dix82] to
compute  -adic approximations to solutions of linear equations
over
-adic approximations to solutions of linear equations
over  . Rational reconstruction modulo
. Rational reconstruction modulo 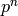 then allows us
to recover the corresponding solutions over
then allows us
to recover the corresponding solutions over  .
.
Algorithm 7.16
Given a matrix  with integer entries and nonzero kernel, this
algorithm computes a nonzero element of
with integer entries and nonzero kernel, this
algorithm computes a nonzero element of 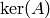 using successive
using successive  -adic approximations.
-adic approximations.
[Prime] Choose a random prime
 .
.[Echelon] Compute the echelon form of
 modulo
modulo  .
.[Done?] If
 has full rank modulo
has full rank modulo  , it has full rank,
so we terminate the algorithm.
, it has full rank,
so we terminate the algorithm.[Setup] Let
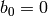 .
.[Iterate] For each
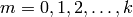 , use the echelon form of
, use the echelon form of
 modulo
modulo  to find a vector
to find a vector 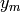 with integer entries such
that
with integer entries such
that 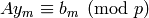 , and then set
, and then set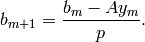
(If
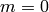 , choose
, choose 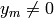 .)
.)[
 -adic Solution]
Let
-adic Solution]
Let 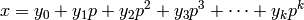 .
.[Lift] Use rational reconstruction (Algorithm 7.4) to find a vector
 with rational entries such that
with rational entries such that
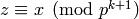 , if such a vector exists. If the vector does
not exist, increase
, if such a vector exists. If the vector does
not exist, increase  or use a different
or use a different  . Otherwise,
output
. Otherwise,
output  .
.
Proof
We verify the case 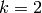 only.
We have
only.
We have 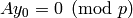 and
and 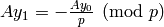 .
Thus
.
Thus
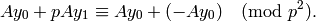
Decomposition Using Kernels¶
We now know enough to give an algorithm to solve Problem Problem 7.11.
Algorithm 7.17
Given an 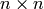 matrix
matrix  over a field
over a field 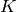 as
in Problem 7.11,
this algorithm computes the
decomposition of
as
in Problem 7.11,
this algorithm computes the
decomposition of  as a direct sum of
simple
as a direct sum of
simple ![K[T]](_images/math/7619d30d16974a3af86a1e8c76839bbba3370b99.png) modules.
modules.
- [Minimal Polynomial] Compute the minimal polynomial
 of
of  ,
e.g., using the multimodular Wiedemann algorithm.
,
e.g., using the multimodular Wiedemann algorithm. - [Factorization] Factor
 using the
algorithm in Section Polynomial Factorization.
using the
algorithm in Section Polynomial Factorization. - [Compute Kernels]
For each irreducible factor
 of
of  , compute
the following.
, compute
the following.- Compute the matrix
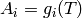 .
. - Compute
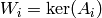 , e.g., using Algorithm 7.16.
, e.g., using Algorithm 7.16.
- Compute the matrix
- [Output Answer] Then
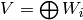 .
.
Remark 7.18
As mentioned in Remark Remark 7.12,
if one can compute such decompositions 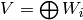 , then
one can easily factor polynomials
, then
one can easily factor polynomials  ; hence the difficulty of
polynomial factorization
is a lower bound on the complexity of writing
; hence the difficulty of
polynomial factorization
is a lower bound on the complexity of writing  as a direct sum of simples.
as a direct sum of simples.
Exercises¶
Exercise 7.1
Given a subspace  of
of 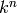 , where
, where  is a field and
is a field and
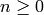 is an integer, give an algorithm to find
a matrix
is an integer, give an algorithm to find
a matrix  such that
such that 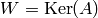 .
.
Exercise 7.2
If 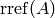 denotes the row reduced echelon form of
denotes the row reduced echelon form of  and
and  is a prime not dividing any denominator
of any entry of
is a prime not dividing any denominator
of any entry of  or of
or of 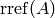 , is
, is
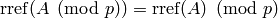 ?
?
Exercise 7.3
Let  be a matrix with entries in
be a matrix with entries in  . Prove that
for all but finitely many primes
. Prove that
for all but finitely many primes  we have
we have
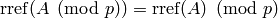 .
.
Exercise 7.4
Let
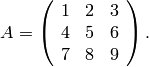
- Compute the echelon form of
 using each of Algorithm 7.3, Algorithm 7.6,
and Algorithm 7.8.
using each of Algorithm 7.3, Algorithm 7.6,
and Algorithm 7.8. - Compute the kernel of
 .
. - Find the characteristic polynomial of
 using the algorithm of Section Wiedemann’s Minimal Polynomial Algorithm.
using the algorithm of Section Wiedemann’s Minimal Polynomial Algorithm.
Exercise 7.5
The notion of echelon form extends to matrices whose entries come
from certain rings other than fields, e.g., Euclidean domains. In
the case of matrices over 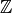 we define a matrix to be in echelon
form (or Hermite normal form) if it satisfies
we define a matrix to be in echelon
form (or Hermite normal form) if it satisfies
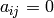 , for
, for 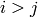 ,
,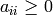 ,
,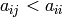 for all
for all 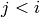 (unless
(unless 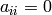 , in which case all
, in which case all 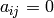 ).
).
There are algorithms for computing with finitely generated
modules over 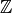 that are analogous to the ones in this chapter
for vector spaces, which depend on computation of Hermite
forms.
that are analogous to the ones in this chapter
for vector spaces, which depend on computation of Hermite
forms.
- Show that the Hermite form of
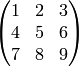 is
is
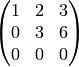 .
. - Describe an algorithm for transforming
an
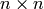 matrix
matrix  with integer entries
into Hermite form using row
operations and the Euclidean algorithm.
with integer entries
into Hermite form using row
operations and the Euclidean algorithm.
Footnotes
| [1] | Allan Steel also invented a similar algorithm. |