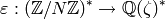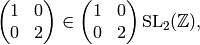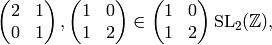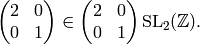General Modular Symbols¶
In this chapter we explain how to generalize the notion of modular symbols given in Chapter Modular Forms of Weight 2 to higher weight and more general level. We define Hecke operators on them and their relation to modular forms via the integration pairing. We omit many difficult proofs that modular symbols have certain properties and instead focus on how to compute with modular symbols. For more details see the references given in this section (especially [Mer94]) and [Wie05].
Modular symbols are a formalism that make it
elementary to compute with homology or cohomology related to certain
Kuga-Sato varieties (these are 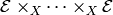 ,
where
,
where  is a modular curve and
is a modular curve and  is the universal elliptic curve
over it). It is not necessary to know anything about these Kuga-Sato
varieties in order to compute with modular symbols.
is the universal elliptic curve
over it). It is not necessary to know anything about these Kuga-Sato
varieties in order to compute with modular symbols.
This chapter is about spaces of modular symbols and how to compute with them. It is by far the most important chapter in this book. The algorithms that build on the theory in this chapter are central to all the computations we will do later in the book.
This chapter closely follows Lo”{i}c Merel’s paper [Mer94].
First we define modular symbols of weight 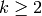 . Then we define
the corresponding Manin symbols and state a theorem of
Merel-Shokurov, which gives all relations between Manin symbols. (The
proof of the Merel-Shokurov theorem is beyond the scope of this book
but is presented nicely in [Wie05].)
Next we describe how the Hecke operators act on both modular and Manin
symbols and how to compute trace and inclusion maps between spaces of
modular symbols of different levels.
. Then we define
the corresponding Manin symbols and state a theorem of
Merel-Shokurov, which gives all relations between Manin symbols. (The
proof of the Merel-Shokurov theorem is beyond the scope of this book
but is presented nicely in [Wie05].)
Next we describe how the Hecke operators act on both modular and Manin
symbols and how to compute trace and inclusion maps between spaces of
modular symbols of different levels.
Not only are modular symbols useful for computation, but they have
been used to prove theoretical results about modular forms. For
example, certain technical calculations with modular symbols are used
in Lo”{i}c Merel’s proof of the uniform boundedness conjecture for
torsion points on elliptic curves over number fields (modular symbols
are used to understand linear independence of Hecke
operators). Another example is [Gri05], which
distills hypotheses about Kato’s Euler system in 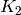 of modular
curves to a simple formula involving modular symbols (when the
hypotheses are satisfied, one obtains a lower bound on the
Shafarevich-Tate group of an elliptic curve).
of modular
curves to a simple formula involving modular symbols (when the
hypotheses are satisfied, one obtains a lower bound on the
Shafarevich-Tate group of an elliptic curve).
Modular Symbols¶
We recall from Chapter Modular Forms of Weight 2
the free abelian group 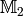 of modular symbols.
We view these as elements of the relative
homology of the extended upper half plane
of modular symbols.
We view these as elements of the relative
homology of the extended upper half plane
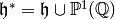 relative to the cusps.
The group
relative to the cusps.
The group 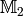 is the free abelian group on symbols
is the free abelian group on symbols 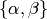 with
with
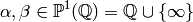
modulo the relations
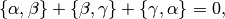
for all 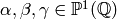 , and all torsion.
More precisely,
, and all torsion.
More precisely,
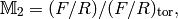
where  is the free abelian group on all pairs
is the free abelian group on all pairs
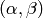 and
and  is the subgroup generated by all elements of
the form
is the subgroup generated by all elements of
the form 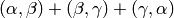 .
Note that
.
Note that 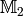 is a huge free abelian group of countable rank.
is a huge free abelian group of countable rank.
For any integer 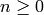 , let
, let
![\Z[X,Y]_n](_images/math/5b9e60a40ec8663f7ade0ab999dac4a8a83352eb.png) be the abelian group of homogeneous polynomials of
degree
be the abelian group of homogeneous polynomials of
degree  in two variables
in two variables 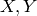 .
.
Remark 1.22
Note that ![\Z[X,Y]_n](_images/math/5b9e60a40ec8663f7ade0ab999dac4a8a83352eb.png) is isomorphic
to
is isomorphic
to 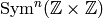 as a group, but certain natural actions are
different. In [Mer94], Merel
uses the notation
as a group, but certain natural actions are
different. In [Mer94], Merel
uses the notation ![\Z_{n}[X,Y]](_images/math/f5bd5b52ff6e9e94a97a9dd9f1644bde2ae4c4b3.png) for what we
denote by
for what we
denote by ![\Z[X,Y]_{n}](_images/math/230c3f9b9c9bf2e49ccc6721a3faa1f02ff74844.png) .
.
Now fix an integer 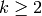 . Set
. Set
![\sM_k = \Z[X,Y]_{k-2} \tensor_\Z \sM_2,](_images/math/a8bfb4b22fc3e9022b856cb38e896c916c057b2c.png)
which is a torsion-free abelian group whose elements are
sums of expressions of the form 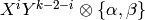 .
For example,
.
For example,
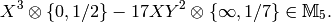
Fix a finite index subgroup  of
of  .
Define a left action of
.
Define a left action of  on
on ![\Z[X,Y]_{k-2}](_images/math/a9324272819ac453b8e5c0ca3d0c8ec01cf8a577.png) as follows. If
as follows. If
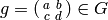 and
and ![P(X,Y)\in \Z[X,Y]_{k-2}](_images/math/e44be5318548c58384d0c35ce502fc54e1316300.png) , let
, let
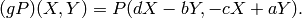
Note that if we think of 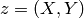 as a column vector, then
as a column vector, then
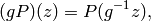
since 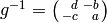 . The reason
for the inverse is so that this is a left action instead of a right
action, e.g., if
. The reason
for the inverse is so that this is a left action instead of a right
action, e.g., if 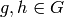 , then
, then
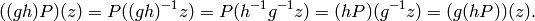
Recall that we let  act on the left on
act on the left on 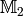 by
by
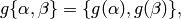
where  acts via linear fractional transformations,
so if
acts via linear fractional transformations,
so if 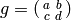 , then
, then
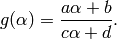
For example, useful special cases to remember are that if 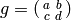 , then
, then
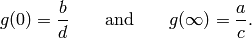
(Here we view  as
as 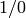 in order to describe the
action.)
in order to describe the
action.)
We now combine these two actions to obtain a left action of  on
on 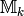 ,
which is given by
,
which is given by
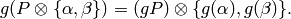
For example,
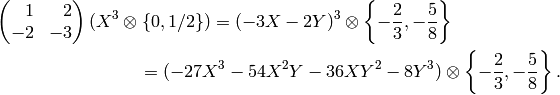
We will often write
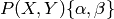 for
for 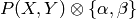 .
.
Definition 1.23
Let 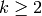 be an integer and let
be an integer and let  be a finite index subgroup of
be a finite index subgroup of  .
The space
.
The space 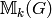 of weight
of weight  modular symbols for
modular symbols for  is the quotient of
is the quotient of
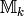 by all relations
by all relations 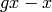 for
for 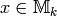 ,
, 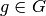 , and by any torsion.
, and by any torsion.
Note that 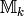 is a torsion-free abelian group, and it is a
nontrivial fact that
is a torsion-free abelian group, and it is a
nontrivial fact that 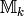 has finite rank. We denote modular
symbols for
has finite rank. We denote modular
symbols for  in exactly the same way we denote elements of
in exactly the same way we denote elements of 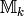 ;
the group
;
the group  will be clear from context.
will be clear from context.
The space of modular symbols over a ring  is
is
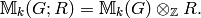
Manin Symbols¶
Let  be a finite index subgroup of
be a finite index subgroup of  and
and 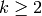 an integer.
Just as in Chapter Modular Forms of Weight 2 it is possible to compute
an integer.
Just as in Chapter Modular Forms of Weight 2 it is possible to compute
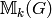 using a computer, despite that, as defined above,
using a computer, despite that, as defined above,
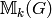 is the quotient of one infinitely generated abelian group
by another one. This section is about Manin symbols, which are a
distinguished subset of
is the quotient of one infinitely generated abelian group
by another one. This section is about Manin symbols, which are a
distinguished subset of 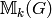 that lead to a finite presentation
for
that lead to a finite presentation
for 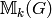 . Formulas written in terms of Manin symbols are
frequently much easier to compute using a computer than formulas in
terms of modular symbols.
. Formulas written in terms of Manin symbols are
frequently much easier to compute using a computer than formulas in
terms of modular symbols.
Suppose ![P\in \Z[X,Y]_{k-2}](_images/math/c004809fdb93273e52b7dcf7cd42a6c477a8a83a.png) and
and 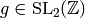 .
Then the Manin symbol associated to this
pair of elements is
.
Then the Manin symbol associated to this
pair of elements is
![[P,g] = g(P\{0,\infty\}) \in \sM_k(G).](_images/math/63419a634500f48284f39fd6e421ea3b39886b4f.png)
Notice that if 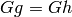 , then
, then ![[P,g] = [P,h]](_images/math/64aae1059073aa276241f2852d1099a4fcac5c60.png) , since
the symbol
, since
the symbol 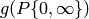 is invariant
by the action of
is invariant
by the action of  on the left (by definition,
since it is a modular symbol for
on the left (by definition,
since it is a modular symbol for  ).
Thus for a right coset
).
Thus for a right coset 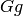 it makes sense to
write
it makes sense to
write ![[P, Gg]](_images/math/21959b833d682c8d2983050da44f60298f63be76.png) for the symbol
for the symbol ![[P,h]](_images/math/221b615b82a0f46a99cc90e371f8a3c711cdd914.png) for any
for any 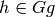 .
Since
.
Since  has finite index in
has finite index in  ,
the abelian group generated by Manin symbols is of finite rank, generated by
,
the abelian group generated by Manin symbols is of finite rank, generated by
![\bigl\{ [X^{k-2-i}Y^i, \, Gg_j] \, : \, i = 0,\ldots, k-2 \quad\text{and}\quad j = 0,\ldots, r \bigr\},](_images/math/dfe25a6139bec3bf7dc69abd111bc489692047c1.png)
where 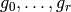 run through representatives for the
right cosets
run through representatives for the
right cosets 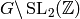 .
.
We next show that every modular symbol can be written as
a 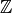 -linear combination of Manin symbols,
so they generate
-linear combination of Manin symbols,
so they generate 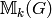 .
.
Proposition 1.24
The Manin symbols generate 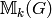 .
.
Proof
The proof if very similar to that
of Proposition 3.11 except we introduce an
extra twist to deal with the polynomial part.
Suppose that we are given a modular
symbol 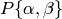 and wish to represent it as a
sum of Manin symbols. Because
and wish to represent it as a
sum of Manin symbols. Because
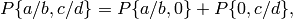
it suffices to write 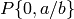 in
terms of Manin symbols.
Let
in
terms of Manin symbols.
Let
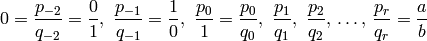
denote the continued fraction convergents of the
rational number 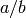 .
Then
.
Then
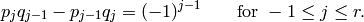
If we let
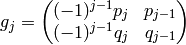 ,
then
,
then 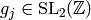 and
and
![P\{0,a/b\}
&=P\sum_{j=-1}^{r}\left\{\frac{p_{j-1}}{q_{j-1}},\frac{p_j}{q_j}\right\}\\
&=\sum_{j=-1}^{r} g_j((g_j^{-1}P)\{0,\infty\})\\
&=\sum_{j=-1}^{r} [g_j^{-1}P,\,\,g_j].](_images/math/2e266b2845256cb60a16d1fc51567dd4b4991219.png)
Since 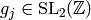 and
and 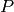 has integer coefficients,
the polynomial
has integer coefficients,
the polynomial 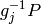 also has integer coefficients,
so we introduce no denominators.
also has integer coefficients,
so we introduce no denominators.
Now that we know the Manin symbols generate 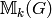 , we
next consider the relations between Manin symbols. Fortunately,
the answer is fairly simple (though the proof is not). Let
, we
next consider the relations between Manin symbols. Fortunately,
the answer is fairly simple (though the proof is not). Let
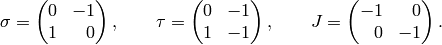
Define a right action of  on Manin symbols
as follows. If
on Manin symbols
as follows. If 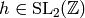 , let
, let
![[P, g]h = [h^{-1} P, gh].](_images/math/a8e843b922349d137fc6063fd055e68bb39dead9.png)
This is a right action because both 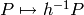 and
and 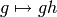 are right actions.
are right actions.
Theorem 1.25
If  is a Manin symbol, then
is a Manin symbol, then
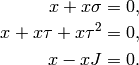
Moreover, these are all the relations between Manin symbols, in the
sense that the space 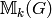 of modular symbols is isomorphic to
the quotient of the free abelian group on the finitely many symbols
of modular symbols is isomorphic to
the quotient of the free abelian group on the finitely many symbols
![[X^{i}Y^{k-2-i},Gg]](_images/math/3aff7d2fef9fdb1d42dd4728904be62bf7ce4415.png) (for
(for 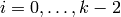 and
and
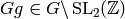 ) by the above relations and any torsion.
) by the above relations and any torsion.
Proof
First we prove that the Manin symbols satisfy the above relations. We follow Merel’s proof (see [Mer94, Section 1.2]). Note that
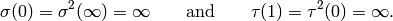
Writing ![x=[P,g]](_images/math/6b3803bc751eec0dfc102607a5790dba0838aa92.png) , we have
, we have
![[P,g] + [P,g]\sigma &=
[P,g] + [\sigma^{-1}P, g\sigma]\\
&= g(P\{0,\infty\}) + g\sigma (\sigma^{-1}P \{0,\infty\})\\
&=
(gP) \{ g(0), g(\infty) \} +
(g\sigma)(\sigma^{-1} P)\{ g\sigma(0), g\sigma(\infty)\} \\
&= (gP) \{ g(0), g(\infty) \} +
(gP)\{ g(\infty), g(0)\} \\
&= (gP)\{ g(0), g(\infty) \} + \{ g(\infty), g(0)\})\\
&= 0.](_images/math/fb61f47065c6df67ac3052f5978677163216a51a.png)
Also,
![[P,g] &+ [P,g]\tau + [P,g]\tau^2 =
[P,g] + [\tau^{-1}P, g\tau] + [\tau^{-2}P, g\tau^2]\\
&=
g(P\{0,\infty\}) +
g\tau(\tau^{-1}P \{0,\infty\})
+ g\tau^2(\tau^{-2}P \{0,\infty\}) \\
&= (gP) \{ g(0), g(\infty) \} +
(gP) \{ g \tau(0),g\tau(\infty)\}
+ (gP) \{ g\tau^2(0),\tau^2(\infty)\} \\
&= (gP) \{ g(0), g(\infty) \} +
(gP) \{ g(1),g(0)\})
+ (gP) \{ g(\infty), g(1)\} \\
&= (gP)\bigl(\{ g(0), g(\infty)\} +
\{ g(\infty), g(1)\} + \{ g(1),g(0)\}\bigr) \\
&= 0.](_images/math/31e598c5ae7d78904859b94dbcab66a1a01fbdf3.png)
Finally,
![[P,g] + [P,g]J &=
g(P\{0,\infty\}) - gJ(J^{-1} P \{gJ(0), gJ(\infty)\}\\
&= (gP)\{g(0),g(\infty)\} - (gP) \{g(0),g(\infty)\}\\
&= 0,](_images/math/35f9388a5f953580a79ab21c15c2087a3fe1f8e2.png)
where we use that 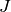 acts trivially via linear fractional
transformations. This proves that the
listed relations are all satisfied.
acts trivially via linear fractional
transformations. This proves that the
listed relations are all satisfied.
That the listed relations are all relations is more difficult to
prove. One
approach is to show (as in [Mer94, Section 1.3]) that the quotient
of Manin symbols by the above relations and torsion is isomorphic to a
space of Shokurov symbols, which is in turn isomorphic to
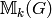 . A much better approach is to apply some results
from group cohomology, as in
[Wie05].
. A much better approach is to apply some results
from group cohomology, as in
[Wie05].
If  is a finite index subgroup and we have an algorithm to
enumerate the right cosets
is a finite index subgroup and we have an algorithm to
enumerate the right cosets 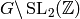 and to decide
which coset an arbitrary element of
and to decide
which coset an arbitrary element of  belongs to, then
Theorem 1.25 and the algorithms of Chapter Linear Algebra
yield an algorithm to compute
belongs to, then
Theorem 1.25 and the algorithms of Chapter Linear Algebra
yield an algorithm to compute 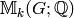 .
Note that if
.
Note that if 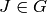 , then the relation
, then the relation 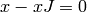 is automatic.
is automatic.
Remark 1.26
The matrices 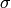 and
and 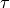 do not commute,
so in computing
do not commute,
so in computing 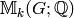 ,
one cannot first quotient out by the two-term
,
one cannot first quotient out by the two-term 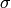 relations, then quotient out only the remaining free generators
by the
relations, then quotient out only the remaining free generators
by the 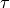 relations, and get the right answer in general.
relations, and get the right answer in general.
Coset Representatives and Manin Symbols¶
The following is analogous to Proposition 3.10:
Proposition 1.27
The right cosets 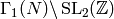 are in bijection
with pairs
are in bijection
with pairs 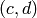 where
where 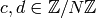 and
and 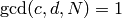 .
The coset containing
a matrix
.
The coset containing
a matrix 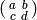 corresponds to
corresponds to 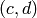 .
.
Proof
This proof is copied from [Cre92, pg. 203],
except in that paper Cremona works with
the analogue of  in
in  , so
his result is slightly different.
Suppose
, so
his result is slightly different.
Suppose  ,
for
,
for  .
We have
.
We have
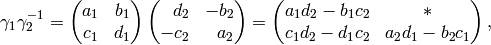
which is in  if and only if
if and only if
(1)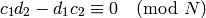
and
(2)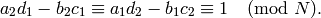
Since the 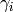 have determinant
have determinant  , if
, if 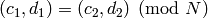 ,
then the congruences (1)–(2) hold.
Conversely, if (1)–(2) hold, then
,
then the congruences (1)–(2) hold.
Conversely, if (1)–(2) hold, then
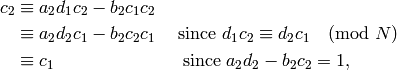
and likewise
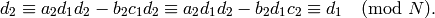
Thus we may view weight  Manin symbols for
Manin symbols for  as triples
of integers
as triples
of integers 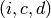 , where
, where 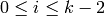 and
and 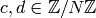 with
with 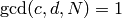 . Here
. Here 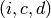 corresponds to the Manin symbol
corresponds to the Manin symbol
![[X^iY^{k-2-i}, \abcd{a}{b}{c'}{d'}]](_images/math/6b7205ff55457880f9cec011200c9955fcbc7f32.png) , where
, where 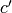 and
and 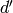 are
congruent to
are
congruent to 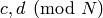 . The relations of
Theorem 1.25 become
. The relations of
Theorem 1.25 become
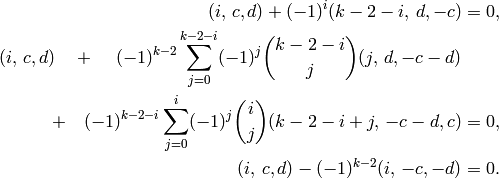
Recall that Proposition 3.10
gives a similar description for  .
.
Modular Symbols with Character¶
Suppose 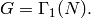 Define an action of diamond-bracket operators
Define an action of diamond-bracket operators 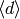 o,
with
o,
with 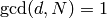 on
Manin symbols as follows:
on
Manin symbols as follows:
![\langle d \rangle ([P,(u,v)]) = \left[P,(du, dv)\right].](_images/math/b5363f8809a513dc582704c89802f4a39b5c3e46.png)
Let
be a Dirichlet character, where 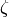 is
an
is
an 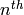 root of unity and
root of unity and  is the order of
is the order of  .
Let
.
Let 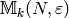 be the quotient of
be the quotient of
![\sM_k(\Gamma_1(N);\Z[\zeta])](_images/math/86b423cade7cce81c0d24ce0ef8c34314e6c4c48.png) by the relations (given
in terms of Manin symbols)
by the relations (given
in terms of Manin symbols)
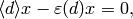
for all ![x\in \sM_k(\Gamma_1(N);\Z[\zeta])](_images/math/80c820ee478e3ab97c1058691c231f083e2edc50.png) ,
,
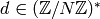 , and by any
, and by any 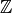 -torsion.
Thus
-torsion.
Thus 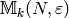 is a
is a ![\Z[\eps]](_images/math/0eea7aad9822a2bd7ceabad9ddf26ba553f62002.png) -module
that has no torsion when viewed as a
-module
that has no torsion when viewed as a 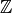 -module.
-module.
Hecke Operators¶
Suppose  is a subgroup of
is a subgroup of  of level
of level  that contains
that contains  .
Just as for modular forms, there is a commutative Hecke algebra
.
Just as for modular forms, there is a commutative Hecke algebra
![\T=\Z[T_1,T_2, \ldots]](_images/math/a10276e35a525005fbee7d9ee05ae1c88c9d012a.png) , which is the subring of
, which is the subring of 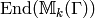 generated by all Hecke operators.
Let
generated by all Hecke operators.
Let
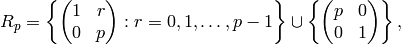
where we omit 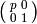 if
if 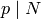 . Then
the Hecke operator
. Then
the Hecke operator  on
on 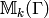 is given by
is given by
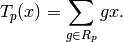
Notice when 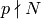 that
that  is defined by summing over
is defined by summing over
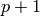 matrices that correspond to the
matrices that correspond to the 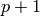 subgroups of
subgroups of 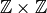 of index
of index  . This is exactly how we defined
. This is exactly how we defined  on modular forms
in Definition Definition 2.26.
on modular forms
in Definition Definition 2.26.
General Definition of Hecke Operators¶
Let  be a finite index subgroup of
be a finite index subgroup of  and suppose
and suppose
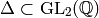
is a set such that  and
and 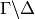 is finite. For example,
is finite. For example, 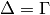 satisfies this condition. Also,
if
satisfies this condition. Also,
if 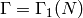 , then for any positive integer
, then for any positive integer  , the set
, the set
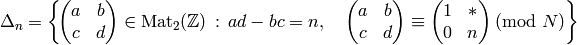
also satisfies this condition, as we will now prove.
Lemma 1.28
We have
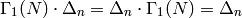
and
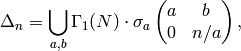
where 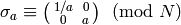 ,
the union is disjoint and
,
the union is disjoint and  with
with  ,
,  ,
and
,
and  . In particular, the set of cosets
. In particular, the set of cosets
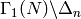 is finite.
is finite.
Proof
(This is Lemma 1 of [Mer94, Section 2.3].)
If 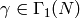 and
and 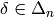 , then
, then
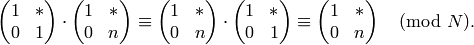
Thus 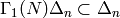 , and since
, and since  is a group,
is a group, 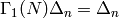 ; likewise
; likewise
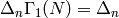 .
.
For the coset decomposition, we first prove the statement for 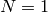 , i.e., for
, i.e., for
 . If
. If  is an arbitrary element
of
is an arbitrary element
of  with determinant
with determinant  , then using row operators on the left
with determinant
, then using row operators on the left
with determinant  , i.e., left multiplication by elements of
, i.e., left multiplication by elements of  ,
we can transform
,
we can transform  into the form
into the form 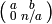 , with
, with
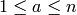 and
and 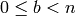 . (Just imagine applying the Euclidean
algorithm to the two entries in the first column of
. (Just imagine applying the Euclidean
algorithm to the two entries in the first column of  . Then
. Then  is the
is the 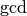 of the two entries in the first column, and the lower left
entry is
of the two entries in the first column, and the lower left
entry is  . Next subtract
. Next subtract 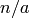 from
from 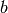 until
until 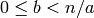 .)
.)
Next suppose  is arbitrary. Let
is arbitrary. Let 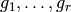 be such
that
be such
that
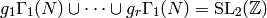
is a disjoint union. If 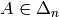 is arbitrary, then
as we showed above, there is some
is arbitrary, then
as we showed above, there is some 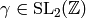 , so that
, so that
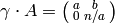 , with
, with 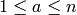 and
and
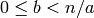 , and
, and 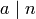 . Write
. Write 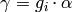 , with
, with 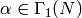 .
Then
.
Then
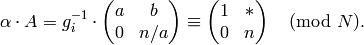
It follows that
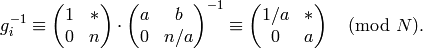
Since 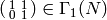 and
and 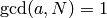 ,
there is
,
there is 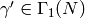 such
that
such
that
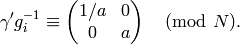
We may then choose 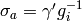 .
Thus every
.
Thus every  is of the form
is of the form
 ,
with
,
with  and
and  suitably bounded. This
proves the second claim.
suitably bounded. This
proves the second claim.
Let any element  act on the left on modular symbols
act on the left on modular symbols  by
by
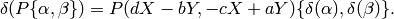
(Until now we had only defined an action of  on modular symbols.)
For
on modular symbols.)
For 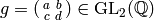 , let
, let
(3)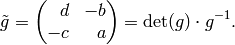
Note that 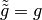 .
Also,
.
Also, 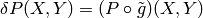 ,
where we set
,
where we set
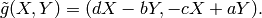
Suppose  and
and  are as above. Fix
a finite set
are as above. Fix
a finite set  of representatives for
of representatives for 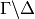 .
Let
.
Let
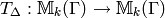
be the linear map
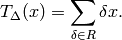
This map is well defined because
if 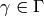 and
and 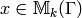 ,
then
,
then
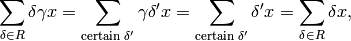
where we have used that 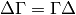 , and
, and
 acts trivially on
acts trivially on 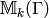 .
.
Let 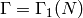 and
and 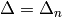 . Then the
. Then the 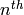 Hecke operator
Hecke operator  is
is 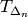 , and by Lemma 1.28,
, and by Lemma 1.28,
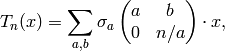
where 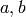 are as in Lemma 1.28.
are as in Lemma 1.28.
Given this definition, we can compute the Hecke operators on
 as follows. Write
as follows. Write  as a modular symbol
as a modular symbol
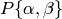 , compute
, compute 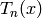 as a modular symbol,
and then convert to Manin symbols using continued fractions
expansions. This is extremely inefficient; fortunately Lo”{i}c
Merel (following [Maz73]) found a much better way, which
we now describe (see [Mer94]).
as a modular symbol,
and then convert to Manin symbols using continued fractions
expansions. This is extremely inefficient; fortunately Lo”{i}c
Merel (following [Maz73]) found a much better way, which
we now describe (see [Mer94]).
Hecke Operators on Manin Symbols¶
If  is a subset of
is a subset of 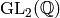 ,
let
,
let
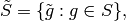
where 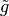 is as in (3).
Also, for any ring
is as in (3).
Also, for any ring  and any subset
and any subset 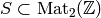 ,
let
,
let ![R[S]](_images/math/de20eacb8a083748cf5fd4fd578dbd6079d1faed.png) denote the free
denote the free  -module with basis the elements of
-module with basis the elements of  ,
so the elements of
,
so the elements of ![R[S]](_images/math/de20eacb8a083748cf5fd4fd578dbd6079d1faed.png) are the finite
are the finite  -linear combinations
of the elements of
-linear combinations
of the elements of  .
.
One of the main theorems of [Mer94] is that for any
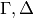 satisfying the condition at the beginning of
Section General Definition of Hecke Operators, if we can find
satisfying the condition at the beginning of
Section General Definition of Hecke Operators, if we can find ![\sum u_M M \in
\C[\Mat_2(\Z)]](_images/math/25141c42b9205d46889606e52c969c97d9ce8af1.png) and a map
and a map
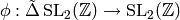
that satisfies certain conditions, then for any Manin
symbol ![[P,g] \in \M_k(\Gamma)](_images/math/bbc47b2db4d2eb2a5757d43e269619a3a9ef09c2.png) , we have
, we have
![T_\Delta([P,g]) =
\sum_{gM\in \tilde{\Delta}\SL_2(\Z)\text{ with }M\in\SL_2(\Z)} u_M
[\tilde{M}\cdot P,\,\, \phi(gM)].](_images/math/1f8cf19d57e827eec52c6b817157e458f3ad6ec6.png)
The paper
[Mer94] contains many examples of 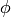 and
and ![\sum u_M M \in
\C[\Mat_2(\Z)]](_images/math/25141c42b9205d46889606e52c969c97d9ce8af1.png) that satisfy all of the conditions.
that satisfy all of the conditions.
When 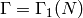 , the complicated list of conditions becomes
simpler. Let
, the complicated list of conditions becomes
simpler. Let 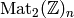 be the set of
be the set of 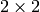 matrices with determinant
matrices with determinant  .
An element
.
An element
![h = \sum u_M [M] \in \C[\Mat_2(\Z)_n]](_images/math/b994a0129c22881338daa6eb10a2cdeebc774e28.png)
satisfies condition 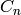 if for every
if for every 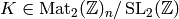 , we have that
, we have that
(4)![\sum_{M \in K} u_M([M\infty] - [M 0 ]) = [\infty] - [0]
\in \C[P^1(\Q)].](_images/math/a6173339113c58a10fabb23cce6433c344396a34.png)
If 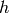 satisfies condition
satisfies condition  , then for any Manin symbol
, then for any Manin symbol
![[P,g] \in M_k(\Gamma_1(N))](_images/math/2c5fc45e9d696ea113824e44e499729de1f7393e.png) , Merel proves that
, Merel proves that
(5)![T_n([P,(u,v)]) = \sum_{M} u_M [P(aX+bY, \, cX+dY), (u,v)M].](_images/math/c5771b3cefd87429dafe6bdbe0646d9b4ab80a3b.png)
Here 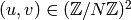 corresponds via Proposition 1.27
to a coset of
corresponds via Proposition 1.27
to a coset of  in
in  , and
if
, and
if 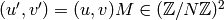 and
and 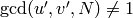 ,
then we omit the corresponding summand.
,
then we omit the corresponding summand.
For example, we will now check directly that the element
![h_2 = \left[\mtwo{2}{0}{0}{1}\right] +
\left[\mtwo{1}{0}{0}{2}\right] +
\left[\mtwo{2}{1}{0}{1}\right] +
\left[\mtwo{1}{0}{1}{2}\right]](_images/math/7009d290f8b9589319ec50f095491bfa0eb9798e.png)
satisfies condition 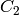 .
We have, as in the proof of Lemma 1.28
(but using elementary column operations), that
.
We have, as in the proof of Lemma 1.28
(but using elementary column operations), that
To verify condition  , we consider in turn each of the three
elements of
, we consider in turn each of the three
elements of  and check that (4)
holds. We have that
and check that (4)
holds. We have that
and
Thus if  , the left
sum of (4) is
, the left
sum of (4) is
![[\abcd{1}{0}{0}{2}(\infty)] - [\abcd{1}{0}{0}{2}(0)] = [\infty]-[0]](_images/math/33bf2e6f6cd021e4134a4630782e88e35cbbc160.png) ,
as required. If
,
as required. If 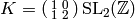 , then
the left side of (4) is
, then
the left side of (4) is
![[\abcd{2}{1}{0}{1}(\infty)] &- [\abcd{2}{1}{0}{1}(0)]
+ [\abcd{1}{0}{1}{2}(\infty)] - [\abcd{1}{0}{1}{2}(0)] \\
&= [\infty] - [1] + [1] - [0] = [\infty] - [0].](_images/math/45cfc80497c7c4e6f1ec57c199a5d67d2402b904.png)
Finally, for 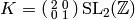 we also have
we also have
![[\abcd{2}{0}{0}{1}(\infty)] - [\abcd{2}{0}{0}{1}(0)] = [\infty]-[0]](_images/math/1d8be5ae4c73aa3b071b79c8b825012a68c4f2d4.png) ,
as required.
Thus by (5) we can compute
,
as required.
Thus by (5) we can compute  on any Manin
symbol, by summing over the action
of the four matrices
on any Manin
symbol, by summing over the action
of the four matrices
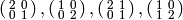 .
.
Proposition 1.29
The element
![\sum_{\substack{a>b\geq 0\\d>c\geq 0\\ad-bc=n}}
\left[\mtwo{a}{b}{c}{d}\right] \in \Z[\Mat_2(\Z)_n]](_images/math/3472e0c1346ecd84617df08dcddf0d9139d2f038.png)
satisfies condition 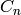 .
.
Merel’s two-page proof of Proposition 1.29 is fairly elementary.
Remark 1.30
In [Cre97a, Section 2.4], Cremona discusses the work of Merel
and Mazur on Heilbronn matrices in the special cases
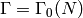 and weight
and weight  . He gives a simple proof
that the action of
. He gives a simple proof
that the action of  on Manin symbols can be computed by summing
the action of some set
on Manin symbols can be computed by summing
the action of some set 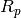 of matrices of determinant
of matrices of determinant  . He
then describes the set
. He
then describes the set 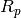 and gives an efficient continued
fractions algorithm for computing it (but he does not prove
that his
and gives an efficient continued
fractions algorithm for computing it (but he does not prove
that his 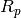 satisfy Merel’s hypothesis).
satisfy Merel’s hypothesis).
Remarks on Complexity¶
Merel gives another family 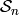 of matrices
that satisfy condition
of matrices
that satisfy condition 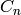 , and he proves that
as
, and he proves that
as 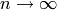 ,
,
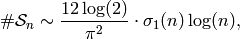
where 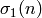 is the sum of the divisors of
is the sum of the divisors of  .
Thus for a fixed space
.
Thus for a fixed space 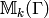 of modular symbols,
one can compute
of modular symbols,
one can compute  using
using
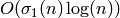 arithmetic operations.
Note that we have fixed
arithmetic operations.
Note that we have fixed 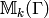 , so we ignore
the linear algebra involved in computation of a presentation; also, adding
elements takes a bounded number of field operations when the space
is fixed. Thus, using Manin symbols
the complexity of computing
, so we ignore
the linear algebra involved in computation of a presentation; also, adding
elements takes a bounded number of field operations when the space
is fixed. Thus, using Manin symbols
the complexity of computing  , for
, for  prime, is
prime, is 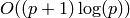 field operations, which is exponential in the number of digits
of
field operations, which is exponential in the number of digits
of  .
.
Basmaji’s Trick¶
There is a trick of Basmaji (see [Bas96]) for computing
a matrix of  on
on 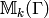 , when
, when  is very large, and it is more
efficient than one might naively expect. Basmaji’s trick does not
improve the big-oh complexity for a fixed space, but it
does improve the
complexity by a constant factor of the dimension of
is very large, and it is more
efficient than one might naively expect. Basmaji’s trick does not
improve the big-oh complexity for a fixed space, but it
does improve the
complexity by a constant factor of the dimension of 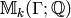 .
Suppose we are interested in computing the matrix for
.
Suppose we are interested in computing the matrix for  for some massive
integer
for some massive
integer  and that
and that 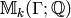 has large dimension.
The trick is as follows. Choose a list
has large dimension.
The trick is as follows. Choose a list
![x_1 =[P_1,g_1],\ldots,x_r = [P_r,g_r] \in V = \sM_k(\Gamma;\Q)](_images/math/61f5419ee928e6c9c6b67edd841c9543169d13fc.png)
of Manin symbols such that the map 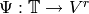 given by
given by
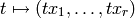
is injective. In practice, it is often possible to do this with  “very small”.
Also, we emphasize that
“very small”.
Also, we emphasize that 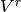 is a
is a  -vector space of dimension
-vector space of dimension
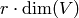 .
.
Next find Hecke operators 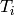 , with
, with  small,
whose images form a basis for the image of
small,
whose images form a basis for the image of 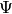 .
Now with the above data precomputed, which only required working with
Hecke operators
.
Now with the above data precomputed, which only required working with
Hecke operators 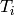 for small
for small  , we are ready to compute
, we are ready to compute  with
with  huge. Compute
huge. Compute 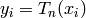 , for each
, for each 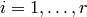 ,
which we can compute using Heilbronn matrices since each
,
which we can compute using Heilbronn matrices since each
![x_i=[P_i,g_i]](_images/math/dd0eca2526d8754efbda36f4cb40e155a9a7a5c5.png) is a Manin symbol. We thus obtain
is a Manin symbol. We thus obtain 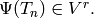 Since we have precomputed Hecke operators
Since we have precomputed Hecke operators 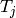 such that
such that
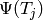 generate
generate 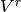 , we can find
, we can find 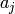 such that
such that
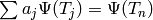 . Then since
. Then since 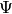 is injective, we have
is injective, we have 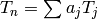 , which gives
the full matrix of
, which gives
the full matrix of  on
on 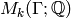 .
.
Cuspidal Modular Symbols¶
Let 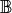 be the free abelian group on symbols
be the free abelian group on symbols 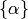 ,
for
,
for 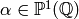 , and set
, and set
![\sB_k = \Z[X,Y]_{k-2}\tensor\sB.](_images/math/ddca2f3bf432936e42f9e44a6f31a65701cb4561.png)
Define a left action of  on
on 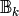 by
by
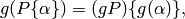
for 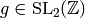 .
For any finite index subgroup
.
For any finite index subgroup 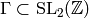 ,
let
,
let
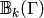 be the quotient of
be the quotient of 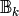 by the relations
by the relations
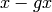 for all
for all 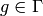 and by any torsion. Thus
and by any torsion. Thus
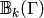 is a torsion-free abelian group.
is a torsion-free abelian group.
The boundary map is the map
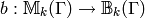
given by extending the map
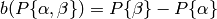
linearly.
The space 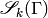 of cuspidal modular symbols
is the kernel
of cuspidal modular symbols
is the kernel
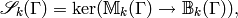
so we have an exact sequence
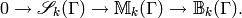
One can prove that when 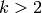 ,
this sequence is exact on the right.
,
this sequence is exact on the right.
Next we give a presentation of 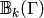 in terms of
“boundary Manin symbols”.
in terms of
“boundary Manin symbols”.
Boundary Manin Symbols¶
We give an explicit description of the boundary
map in terms of Manin symbols for
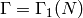 , then describe an
efficient way to compute the boundary map.
, then describe an
efficient way to compute the boundary map.
Let 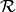 be the equivalence relation
on
be the equivalence relation
on 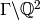 given by
given by
![[\Gamma\smallvtwo{\lambda u}{\lambda v}] \sim
\sign(\lambda)^k[\Gamma\smallvtwo{u}{v}],](_images/math/fcacefbd41a72692db1b7c6361accb82c698c1a6.png)
for any 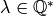 . Denote by
. Denote by 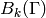 the finite-dimensional
the finite-dimensional  -vector space
with basis the equivalence classes
-vector space
with basis the equivalence classes
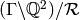 .
The following two propositions are proved in [Mer94].
.
The following two propositions are proved in [Mer94].
Proposition 1.31
The map
![\mu:\sB_k(\Gamma)\ra B_k(\Gamma),
\qquad P\left\{\frac{u}{v}\right\}\mapsto
P(u,v)\left[\Gamma\vtwo{u}{v}\right]](_images/math/9559cf5b615be0e86100a208d28fa2fffe8586f1.png)
is well defined and injective.
Here 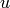 and
and  are assumed coprime.
are assumed coprime.
Thus the kernel of 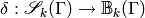 is the same as the kernel of
is the same as the kernel of 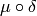 .
.
Proposition 1.32
Let 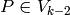 and
and 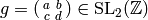 . We have
. We have
![\mu\circ\delta([P,(c,d)])
= P(1,0)[\Gamma\smallvtwo{a}{c}]
-P(0,1)[\Gamma\smallvtwo{b}{d}].](_images/math/d18d366f2bb5581342c7baa2bbd9ffa0439431af.png)
We next describe how to explicitly compute
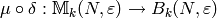 by generalizing the algorithm of [Cre97a, Section 2.2].
To compute the image of
by generalizing the algorithm of [Cre97a, Section 2.2].
To compute the image of ![[P,(c,d)]](_images/math/7ee56748b3815f654fd127c6f4fb0420331cfed4.png) , with
, with
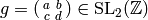 ,
we must compute the class of
,
we must compute the class of ![[\smallvtwo{a}{c}]](_images/math/12560333bc7439a91fe0623e008f6836b93e3f84.png) and of
and of
![[\smallvtwo{b}{d}]](_images/math/26869b643da3caa086a9fad68012b97aafc6ba9f.png) .
Instead of finding a canonical form for cusps, we
use a quick test for equivalence modulo scalars.
In the following algorithm, by the
.
Instead of finding a canonical form for cusps, we
use a quick test for equivalence modulo scalars.
In the following algorithm, by the  symbol we mean
the
symbol we mean
the  basis vector for a basis of
basis vector for a basis of 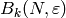 . This
basis is constructed as the algorithm is called successively.
We first give the algorithm, and then prove the facts
used by the algorithm in testing equivalence.
. This
basis is constructed as the algorithm is called successively.
We first give the algorithm, and then prove the facts
used by the algorithm in testing equivalence.
Algorithm 1.33
Given a boundary Manin symbol ![[\smallvtwo{u}{v}],](_images/math/694f8e5701fe7de3d787b83d633af21910bd14b0.png) this algorithm outputs an integer
this algorithm outputs an integer  and a
scalar
and a
scalar 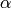 such that
such that ![[\smallvtwo{u}{v}]](_images/math/493bbe978d5477aa4f8cede37b08d420eff2ba7d.png) is equivalent to
is equivalent to 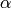 times the
times the 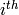 symbol found so far. (We call this algorithm
repeatedly and maintain a running list of cusps seen so far.)
symbol found so far. (We call this algorithm
repeatedly and maintain a running list of cusps seen so far.)
- Use Proposition 3.21 to check
whether or not
![[\smallvtwo{u}{v}]](_images/math/493bbe978d5477aa4f8cede37b08d420eff2ba7d.png) is equivalent, modulo scalars, to
any cusp found. If so, return the representative, its
index, and the scalar. If not, record
is equivalent, modulo scalars, to
any cusp found. If so, return the representative, its
index, and the scalar. If not, record 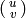 in the
representative list.
in the
representative list. - Using Proposition 1.37,
check whether or not
![[\smallvtwo{u}{v}]](_images/math/493bbe978d5477aa4f8cede37b08d420eff2ba7d.png) is forced to equal
is forced to equal  by the
relations. If it does not equal
by the
relations. If it does not equal  , return its position in the list
and the scalar
, return its position in the list
and the scalar  . If it equals
. If it equals  , return the scalar
, return the scalar  and the
position
and the
position  ; keep
; keep 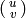 in the list, and record that it
is equivalent to
in the list, and record that it
is equivalent to  .
.
The case considered in Cremona’s book [Cre97a] only involve the trivial character, so no cusp classes are forced to vanish. Cremona gives the following two criteria for equivalence.
Proposition 1.34
Consider 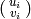 ,
, 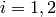 , with
, with 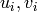 integers such
that
integers such
that 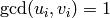 for each
for each  .
.
There exists
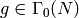 such that
such that
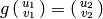 if and only if
if and only if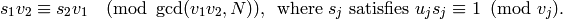
There exists
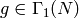 such that
such that
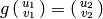 if and only if
if and only if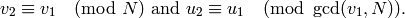
Algorithm 1.35
Suppose 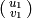 and
and
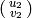 are equivalent modulo
are equivalent modulo  .
This algorithm computes a matrix
.
This algorithm computes a matrix 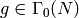 such
that
such
that 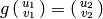 .
.
- Let
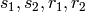 be solutions to
be solutions to
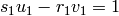 and
and
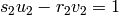 .
. - Find integers
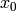 and
and 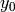 such
that
such
that 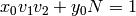 .
. - Let
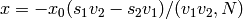 and
and 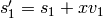 .
. - Output
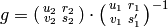 ,
which sends
,
which sends 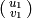 to
to 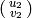 .
.
Proof
See the proof of [Cre97a, Prop. 8.13].
The  relations can make the situation more
complicated, since it is possible that
relations can make the situation more
complicated, since it is possible that
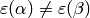 but
but
![\eps(\alp)\left[\vtwo{u}{v}\right] =\left[\gamma_\alp \vtwo{u}{v}\right]=
\left[\gamma_\beta \vtwo{u}{v}\right]=\eps(\beta)\left[\vtwo{u}{v}\right].](_images/math/36b0cc57157698a76d6984c4df7cc86e74ee0217.png)
One way out of this difficulty is to construct
the cusp classes for  , and then quotient
out by the additional
, and then quotient
out by the additional  relations using
Gaussian elimination. This is far too
inefficient to be useful in practice because the number of
relations using
Gaussian elimination. This is far too
inefficient to be useful in practice because the number of
 cusp classes can be unreasonably large.
Instead, we give a quick test to determine whether or not
a cusp vanishes modulo the
cusp classes can be unreasonably large.
Instead, we give a quick test to determine whether or not
a cusp vanishes modulo the  -relations.
-relations.
Lemma 1.36
Suppose 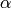 and
and 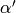 are integers
such that
are integers
such that 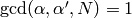 .
Then there exist integers
.
Then there exist integers 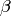 and
and 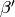 ,
congruent to
,
congruent to 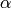 and
and 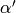 modulo
modulo  , respectively,
such that
, respectively,
such that 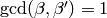 .
.
Proof
By Exercise 1.12 the map
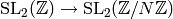 is surjective.
By the Euclidean algorithm, there exist
integers
is surjective.
By the Euclidean algorithm, there exist
integers  ,
,  and
and  such that
such that
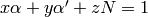 .
Consider the matrix
.
Consider the matrix
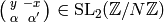 and take
and take 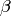 ,
, 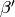 to be the bottom
row of a lift of this matrix to
to be the bottom
row of a lift of this matrix to  .
.
Proposition 1.37
Let  be a positive integer and
be a positive integer and  a Dirichlet
character of modulus
a Dirichlet
character of modulus  .
Suppose
.
Suppose 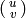 is a cusp with
is a cusp with 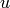 and
and  coprime.
Then
coprime.
Then 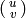 vanishes modulo the relations
vanishes modulo the relations
![\left[\gamma\smallvtwo{u}{v}\right]=
\eps(\gamma)\left[\smallvtwo{u}{v}\right],\qquad
\text{all $\gamma\in\Gamma_0(N)$},](_images/math/c9edd7837260f937bc532809ea7032fa9c7bd104.png)
if and only if there exists 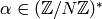 ,
with
,
with 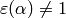 , such that
, such that
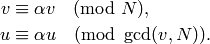
Proof
First suppose such an 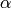 exists.
By Lemma 1.36
there exists
exists.
By Lemma 1.36
there exists 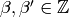 lifting
lifting
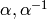 such that
such that 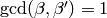 .
The cusp
.
The cusp 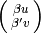 has coprime coordinates so,
by Proposition 1.34 and our
congruence conditions on
has coprime coordinates so,
by Proposition 1.34 and our
congruence conditions on 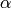 , the cusps
, the cusps
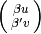 and
and 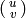 are equivalent by
an element of
are equivalent by
an element of  .
This implies that
.
This implies that ![\left[\smallvtwo{\beta{}u}{\beta'{}v}\right]
=\left[\smallvtwo{u}{v}\right]](_images/math/cd67f0f112bd578d2c3ee985203c072e087f4c9f.png) .
Since
.
Since ![\left[\smallvtwo{\beta{}u}{\beta'{}v}\right]
= \eps(\alp)\left[\smallvtwo{u}{v}\right]](_images/math/47ee1721d0c8c1083e2967dcfa0582d8d2899bc7.png) and
and 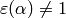 , we have
, we have ![\left[\smallvtwo{u}{v}\right]=0](_images/math/b039b2c8608916f5b455971844e755c53ce7bfe7.png) .
.
Conversely, suppose ![\left[\smallvtwo{u}{v}\right]=0](_images/math/b039b2c8608916f5b455971844e755c53ce7bfe7.png) .
Because all relations are two-term relations and the
.
Because all relations are two-term relations and the
 -relations identify
-relations identify  -orbits,
there must exists
-orbits,
there must exists 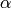 and
and 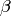 with
with
![\left[\gamma_\alp \vtwo{u}{v}\right]
=\left[\gamma_\beta \vtwo{u}{v}\right]
\qquad\text{ and }\eps(\alp)\ne \eps(\beta).](_images/math/3876ea7329cbbcd61acf5af05d487075376c5030.png)
Indeed, if this did not occur,
then we could mod out by the  relations by writing
each
relations by writing
each ![\left[\gamma_\alp \smallvtwo{u}{v} \right]](_images/math/805f1c5ca7264745717f41d590f554baa4a4a397.png) in terms of
in terms of ![\left[\smallvtwo{u}{v}\right]](_images/math/00e466ff071d039b32e3cf1b80d2546c398caa85.png) , and there would
be no further relations left to kill
, and there would
be no further relations left to kill
![\left[\smallvtwo{u}{v}\right]](_images/math/00e466ff071d039b32e3cf1b80d2546c398caa85.png) .
Next observe that
.
Next observe that
![\left[\gamma_{\beta^{-1}\alp}
\vtwo{u}{v}\right]
&= \left[\gamma_{\beta^{-1}}\gamma_\alp
\vtwo{u}{v}\right]\\
&= \eps(\beta^{-1})\left[\gamma_\alp
\vtwo{u}{v}\right]
= \eps(\beta^{-1})\left[\gamma_\beta
\vtwo{u}{v}\right]
= \left[\vtwo{u}{v}\right].](_images/math/cd694666885caf7a9f1f3e981b4ac41f8b7b032a.png)
Applying Proposition 1.34 and
noting that 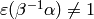 shows
that
shows
that 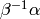 satisfies the properties
of the ”
satisfies the properties
of the ” 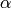 ” in the statement of the
proposition.
” in the statement of the
proposition.
We enumerate the possible 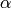 appearing
in Proposition 1.37 as follows.
Let
appearing
in Proposition 1.37 as follows.
Let 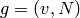 and list the
and list the
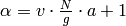 , for
, for 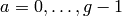 ,
such that
,
such that 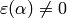 .
.
Pairing Modular Symbols and Modular Forms¶
In this section we define a pairing between modular symbols and modular forms that the Hecke operators respect. We also define an involution on modular symbols and study its relationship with the pairing. This pairing is crucial in much that follows, because it gives rise to period maps from modular symbols to certain complex vector spaces.
Fix an integer weight 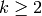 and a finite index subgroup
and a finite index subgroup
 of
of  . Let
. Let 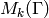 denote the space
of holomorphic modular forms of weight
denote the space
of holomorphic modular forms of weight  for
for  ,
and let
,
and let 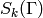 denote its cuspidal subspace.
Following [Mer94, Section 1.5], let
denote its cuspidal subspace.
Following [Mer94, Section 1.5], let
(6)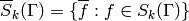
denote the space of antiholomorphic cusp forms. Here
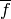 is the function on
is the function on 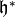 given by
given by
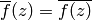 .
.
Define a pairing
(7)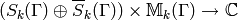
by letting
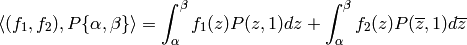
and extending linearly. Here the integral is a complex
path integral along a simple path from 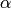 to
to 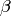 in
in  (so, e.g., write
(so, e.g., write 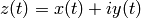 ,
where
,
where 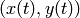 traces out the path and consider
two real integrals).
traces out the path and consider
two real integrals).
Proposition 1.38
The integration pairing is well defined, i.e., if we
replace 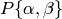 by an equivalent modular symbol
(equivalent modulo the left action of
by an equivalent modular symbol
(equivalent modulo the left action of  ), then the integral
is the same.
), then the integral
is the same.
Proof
This follows from the change of variables formulas
for integration and the fact that 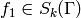 and
and
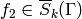 . For example, if
. For example, if 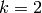 ,
,
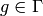 and
and 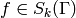 , then
, then
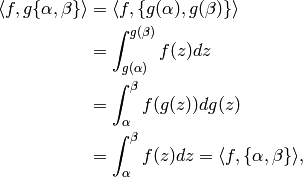
where 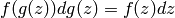 because
because
 is a weight
is a weight  modular form.
For the case of arbitrary weight
modular form.
For the case of arbitrary weight 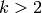 , see
Exercise 1.14.
, see
Exercise 1.14.
The integration pairing is very relevant to the
study of special values of
 -functions. The
-functions. The  -function
of a cusp form
-function
of a cusp form 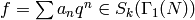 is
is
(8)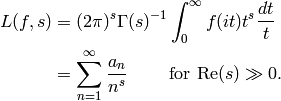
The equality of the integral and the
Dirichlet series follows
by switching the order of summation and integration,
which is justified using standard estimates on 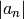 (see, e.g., [Kna92, Section VIII.5]).
(see, e.g., [Kna92, Section VIII.5]).
For each integer 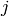 with
with 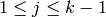 , we have,
setting
, we have,
setting 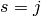 and making the change of variables
and making the change of variables 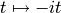 in (8), that
in (8), that
(9)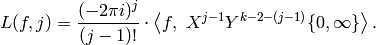
The integers 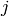 as above are called critical integers.
When
as above are called critical integers.
When  is an eigenform, they have deep
conjectural significance (see [BK90, Sch90]).
One can approximate
is an eigenform, they have deep
conjectural significance (see [BK90, Sch90]).
One can approximate 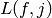 to any desired precision
by computing the above pairing explicitly using
the method described in Chapter Computing Periods.
Alternatively, [Dok04] contains
methods for computing special values of very
general
to any desired precision
by computing the above pairing explicitly using
the method described in Chapter Computing Periods.
Alternatively, [Dok04] contains
methods for computing special values of very
general  -functions, which can be used for
approximating
-functions, which can be used for
approximating 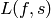 for arbitrary
for arbitrary  , in addition
to just the critical integers
, in addition
to just the critical integers 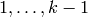 .
.
Theorem 1.39
The pairing
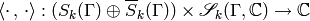
is a nondegenerate pairing of complex vector spaces.
Corollary 1.40
We have
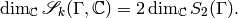
The pairing is also compatible with Hecke operators. Before proving
this, we define an action of Hecke operators on  and
on
and
on 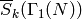 . The definition is similar to the one
we gave in Section Hecke Operators for modular forms of level
. The definition is similar to the one
we gave in Section Hecke Operators for modular forms of level  .
For a positive integer
.
For a positive integer  , let
, let 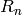 be a set of coset
representatives for
be a set of coset
representatives for 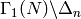 from
Lemma 1.28. For any
from
Lemma 1.28. For any 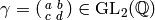 and
and 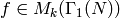 set
set
![f^{[\gamma]_k} = \det(\gamma)^{k-1} (cz+d)^{-k} f(\gamma(z)).](_images/math/bff7a83af850b2fdab4cb1b4e8046e96f6f77d5d.png)
Also, for 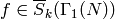 , set
, set
![f^{[\gamma]_k'} = \det(\gamma)^{k-1} (c\zbar+d)^{-k} f(\gamma(z)).](_images/math/48de977b97539384d3146dcc82bbf62a2ffc6aaf.png)
Then for 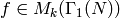 ,
,
![T_n(f) = \sum_{\gamma\in R_n} f^{[\gamma]_k}](_images/math/107c047c94d6c915422bf209aa4a1868afa9fb41.png)
and for 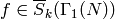 ,
,
![T_n(f) = \sum_{\gamma\in R_n} f^{[\gamma]_k'}.](_images/math/8f2c5ba1e839ace16f527fb48cee5ffcd14ae2fb.png)
This agrees with the definition from Section Hecke Operators
when 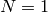 .
.
Remark 1.41
If  is an arbitrary finite index subgroup of
is an arbitrary finite index subgroup of  ,
then we can define operators
,
then we can define operators 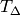 on
on 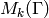 for any
for any  with
with 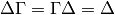 and
and 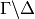 finite. For concreteness we
do not do the general case here or in the theorem below, but
the proof is exactly the same (see [Mer94, Section 1.5]).
finite. For concreteness we
do not do the general case here or in the theorem below, but
the proof is exactly the same (see [Mer94, Section 1.5]).
Finally we prove the promised Hecke compatibility of the pairing. This proof should convince you that the definition of modular symbols is sensible, in that they are natural objects to integrate against modular forms.
Theorem 1.42
If
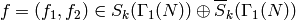
and 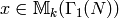 , then for any
, then for any  ,
,
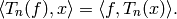
Proof
We follow [Mer94, Section 2.1] (but with more details) and will
only prove the theorem when 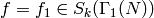 , the proof
in the general case being the same.
, the proof
in the general case being the same.
Let 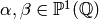 ,
, ![P\in \Z[X,Y]_{k-2}](_images/math/c004809fdb93273e52b7dcf7cd42a6c477a8a83a.png) ,
and for
,
and for 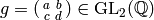 , set
, set
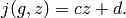
Let  be any positive integer,
and let
be any positive integer,
and let 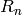 be a set of coset
representatives for
be a set of coset
representatives for 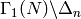 from
Lemma 1.28.
from
Lemma 1.28.
We have
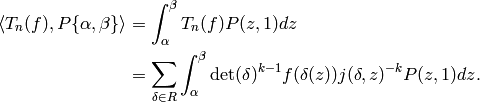
Now for each summand corresponding to the 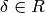 ,
make the change of variables
,
make the change of variables 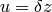 . Thus we
make
. Thus we
make  change of variables.
Also, we will use the notation
change of variables.
Also, we will use the notation
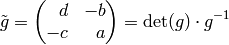
for  .
We have
.
We have
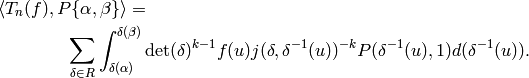
We have 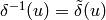 ,
since a linear fractional transformation is unchanged
by a nonzero rescaling of a matrix that induces it.
Thus by the quotient rule, using that
,
since a linear fractional transformation is unchanged
by a nonzero rescaling of a matrix that induces it.
Thus by the quotient rule, using that 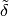 has determinant
has determinant 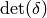 , we see that
, we see that
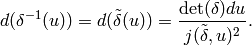
We next show that
(10)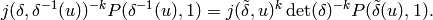
From the definitions, and again using that 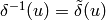 , we see that
, we see that
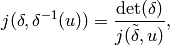
which proves that (10) holds. Thus
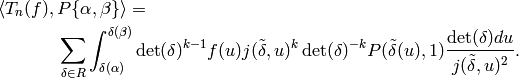
Next we use that
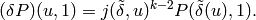
To see this, note that 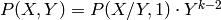 .
Using this we see that
.
Using this we see that
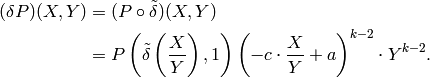
Now substituting 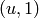 for
for 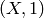 , we see that
, we see that
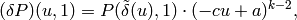
as required. Thus finally
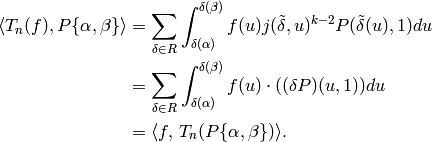
Suppose that  is a finite index
subgroup of
is a finite index
subgroup of  such that
if
such that
if 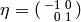 , then
, then
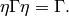
For example, 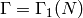 satisfies this condition.
There is an involution
satisfies this condition.
There is an involution 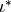 on
on 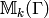 given by
given by
(11)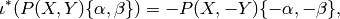
which we call the star involution.
On Manin symbols, 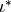 is
is
(12)![\iota^*[P,(u,v)] = -[P(-X,Y), (-u,v)].](_images/math/bf0bd00c3d527d0e21eb74748e3b1bf7913af18a.png)
Let 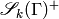 be the
be the 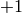 eigenspace for
eigenspace for
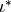 on
on 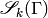 , and let
, and let 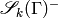 be the
be the 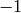 eigenspace.
There is also a map
eigenspace.
There is also a map  on modular forms, which
is adjoint to
on modular forms, which
is adjoint to 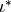 .
.
Remark 1.43
Notice the minus sign in front of 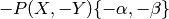 in
(11). This sign is missing in [Cre97a],
which is a potential source of confusion (this is not a mistake,
but a different choice of convention).
in
(11). This sign is missing in [Cre97a],
which is a potential source of confusion (this is not a mistake,
but a different choice of convention).
We now state the final result about the pairing, which explains how modular symbols and modular forms are related.
Theorem 1.44
The integration pairing 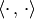 induces
nondegenerate Hecke compatible bilinear pairings
induces
nondegenerate Hecke compatible bilinear pairings
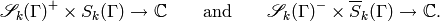
Remark 1.45
We make some remarks about computing
the boundary map of Section Boundary Manin Symbols when working
in the 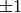 quotient.
Let
quotient.
Let  be a sign, either
be a sign, either 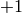 or
or 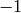 . To compute
. To compute 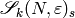 , it is necessary to replace
, it is necessary to replace
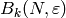 by its quotient modulo the additional relations
by its quotient modulo the additional relations ![\left[
\smallvtwo{-u}{\hfill v}\right] = s \left[\smallvtwo{u}{v}\right]](_images/math/d81c3ef673b68efeca983038c1b41517fb841327.png) for all cusps
for all cusps 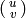 . Algorithm 1.33 can be
modified to deal with this situation as follows. Given a cusp
. Algorithm 1.33 can be
modified to deal with this situation as follows. Given a cusp
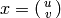 , proceed as in Algorithm 1.33 and
check if either
, proceed as in Algorithm 1.33 and
check if either 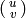 or
or 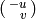 is
equivalent (modulo scalars) to any cusp seen so far. If not, use the
following trick to determine whether the
is
equivalent (modulo scalars) to any cusp seen so far. If not, use the
following trick to determine whether the  and
and  -relations kill
the class of
-relations kill
the class of 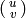 : use the unmodified
Algorithm 1.33 to compute the scalars
: use the unmodified
Algorithm 1.33 to compute the scalars 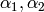 and indices
and indices 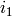 ,
, 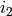 associated to
associated to 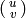 and
and
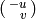 , respectively. The
, respectively. The  -relation kills the
class of
-relation kills the
class of 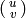 if and only if
if and only if 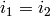 but
but 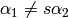 .
.
Degeneracy Maps¶
In this section, we describe natural maps between spaces of modular symbols with character of different levels. We consider spaces with character, since they are so important in applications.
Fix a positive integer  and a Dirichlet
character
and a Dirichlet
character
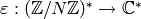 . Let
. Let  be a positive divisor
of
be a positive divisor
of  that is divisible by the conductor of
that is divisible by the conductor of  , in the sense
that
, in the sense
that  factors through
factors through 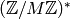 via the natural map
via the natural map
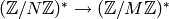 composed with some uniquely defined
character
composed with some uniquely defined
character 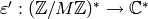 . For any positive divisor
. For any positive divisor 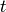 of
of
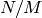 , let
, let 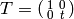 and fix a choice
and fix a choice 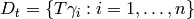 of coset representatives for
of coset representatives for 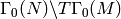 .
.
Remark 1.46
Note that [Mer94, Section 2.6] contains a typo:
The quotient ” 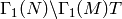 ” should be replaced
by ”
” should be replaced
by ” 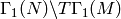 “.
“.
Proposition 1.47
For each divisor 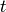 of
of 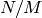 there are well-defined linear maps
there are well-defined linear maps
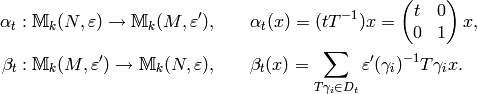
Furthermore,
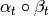 is multiplication by
is multiplication by
![t^{k-2}\cdot [\Gamma_0(M) : \Gamma_0(N)].](_images/math/3d7cfe7d71374bdc3a5a5410c79a119d672b63f0.png)
Proof
To show that 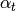 is well defined, we must show that for
each
is well defined, we must show that for
each 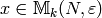 and
and 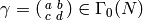 ,
we have
,
we have
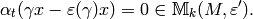
We have
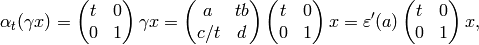
so
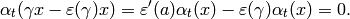
We next verify that 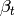 is well defined.
Suppose that
is well defined.
Suppose that 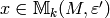 and
and 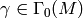 ;
then
;
then 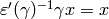 , so
, so
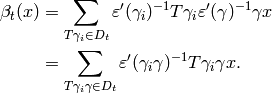
This computation shows that the definition of 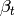 does not depend on the choice
does not depend on the choice 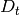 of coset representatives.
To finish the proof that
of coset representatives.
To finish the proof that 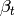 is well defined,
we must show that, for
is well defined,
we must show that, for 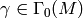 , we have
, we have
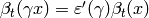 so that
so that 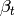 respects the relations that define
respects the relations that define 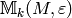 .
Using that
.
Using that 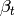 does not depend on the choice of
coset representative, we find that for
does not depend on the choice of
coset representative, we find that for 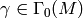 ,
,
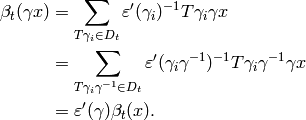
To compute 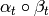 , we use
that
, we use
that ![\#D_t = [\Gamma_0(N) : \Gamma_0(M)]](_images/math/a1f72960e556153105329f88cdbe912fa45a1ea7.png) :
:
![\alp_t(\beta_t(x)) &=
\alp_t \left(\sum_{T\gamma_i}
\eps'(\gamma_i)^{-1}T\gamma_i x\right)\\
&= \sum_{T\gamma_i}
\eps'(\gamma_i)^{-1}(tT^{-1})T\gamma_i x\\
&= t^{k-2}\sum_{T\gamma_i}
\eps'(\gamma_i)^{-1}\gamma_i x\\
&= t^{k-2}\sum_{T\gamma_i} x \\
&= t^{k-2} \cdot [\Gamma_0(N) : \Gamma_0(M)] \cdot x.](_images/math/d0bfeb913223cf3cd16e11dee6a2fe5862102c64.png)
The scalar factor of  appears instead
of
appears instead
of 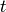 , because
, because 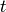 is acting on
is acting on  as an element of
as an element of 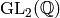 and not as an an element of
and not as an an element of  .
.
Definition 1.48
The space 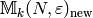 of new modular symbols is the
intersection of the kernels of the
of new modular symbols is the
intersection of the kernels of the 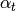 as
as 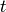 runs through all positive divisors of
runs through all positive divisors of 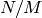 and
and  runs through positive divisors of
runs through positive divisors of  strictly less than
strictly less than  and divisible by the conductor of
and divisible by the conductor of  .
The subspace
.
The subspace 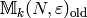 of old modular symbols
is the subspace generated by the images of the
of old modular symbols
is the subspace generated by the images of the 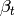 where
where 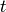 runs through all positive divisors of
runs through all positive divisors of 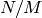 and
and  runs through positive divisors of
runs through positive divisors of  strictly less than
strictly less than  and divisible by the conductor of
and divisible by the conductor of  .
The new and old subspaces of cuspidal modular
symbols are the intersections of the above spaces
with
.
The new and old subspaces of cuspidal modular
symbols are the intersections of the above spaces
with 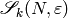 .
.
Example 1.49
The new and old subspaces need not be disjoint, as the following
example illustrates! (This contradicts [Mer94, pg. 80].)
Consider, for example, the case 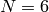 ,
, 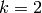 , and trivial character.
The spaces
, and trivial character.
The spaces 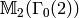 and
and 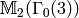 are each of
dimension
are each of
dimension  , and each is generated by the modular symbol
, and each is generated by the modular symbol
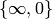 . The space
. The space 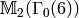 is of dimension
is of dimension  and is generated by the three modular symbols
and is generated by the three modular symbols 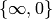 ,
,
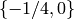 , and
, and 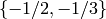 . The space generated by the two
images of
. The space generated by the two
images of 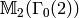 under the two degeneracy maps has
dimension
under the two degeneracy maps has
dimension  , and likewise for
, and likewise for 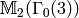 . Together
these images generate
. Together
these images generate 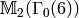 , so
, so 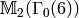 is equal to its old subspace. However, the new subspace is
nontrivial because the two degeneracy maps
is equal to its old subspace. However, the new subspace is
nontrivial because the two degeneracy maps 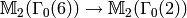 are equal, as are the two degeneracy maps
are equal, as are the two degeneracy maps
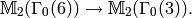
In particular, the
intersection of the kernels of the degeneracy maps has dimension at
least  (in fact, it equals
(in fact, it equals  ).
We verify some of the above claims using Sage.
).
We verify some of the above claims using Sage.
sage: M = ModularSymbols(Gamma0(6)); M
Modular Symbols space of dimension 3 for Gamma_0(6)
of weight 2 with sign 0 over Rational Field
sage: M.new_subspace()
Modular Symbols subspace of dimension 1 of Modular
Symbols space of dimension 3 for Gamma_0(6) of weight
2 with sign 0 over Rational Field
sage: M.old_subspace()
Modular Symbols subspace of dimension 3 of Modular
Symbols space of dimension 3 for Gamma_0(6) of weight
2 with sign 0 over Rational Field
Explicitly Computing 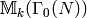 ¶
¶
In this section we explicitly compute 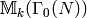 for various
for various
 and
and  . We represent Manin symbols for
. We represent Manin symbols for  as triples
of integers
as triples
of integers 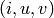 , where
, where 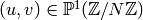 , and
, and 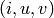 corresponds
to
corresponds
to ![[X^i Y^{k-2-i}, (u,v)]](_images/math/6d24bb9e2eff0259b7df365055c0ee30730f1ba7.png) in the usual notation. Also, recall from
Proposition 3.10 that
in the usual notation. Also, recall from
Proposition 3.10 that 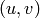 corresponds to the right
coset of
corresponds to the right
coset of  that contains a matrix
that contains a matrix
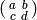 with
with 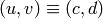 as elements of
as elements of
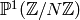 , i.e., up to rescaling by an element of
, i.e., up to rescaling by an element of  .
.
Computing 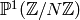 ¶
¶
In this section we give an algorithm to compute a canonical
representative for each element of 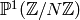 . This algorithm is
extremely important because modular symbols implementations use it a
huge number of times. A more naive approach would be to store all
pairs
. This algorithm is
extremely important because modular symbols implementations use it a
huge number of times. A more naive approach would be to store all
pairs 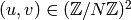 and a fixed reduced representative, but
this wastes a huge amount of memory. For example, if
and a fixed reduced representative, but
this wastes a huge amount of memory. For example, if 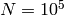 ,
we would store an array of
,
we would store an array of
Another approach to enumerating 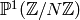 is described at the end
of [Cre97a, Section 2.2]. It uses the fact that is easy to
test whether two pairs
is described at the end
of [Cre97a, Section 2.2]. It uses the fact that is easy to
test whether two pairs 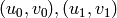 define the same element
of
define the same element
of 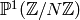 ; they do if and only if we have equality of cross
terms
; they do if and only if we have equality of cross
terms 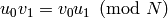 (see
[Cre97a, Prop. 2.2.1]). So we consider the
(see
[Cre97a, Prop. 2.2.1]). So we consider the
 -based list of elements
-based list of elements
(13)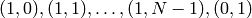
concatenated with the list of nonequivalent elements
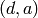 for
for 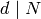 and
and
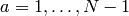 , checking each time we add a new element to our
list (of
, checking each time we add a new element to our
list (of 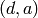 ) whether we have already seen it.
) whether we have already seen it.
Given a random pair 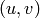 , the problem
is then to find the index of the element of our list of the equivalent
representative in
, the problem
is then to find the index of the element of our list of the equivalent
representative in 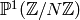 .
We use the following
algorithm, which finds a canonical representative for each element of
.
We use the following
algorithm, which finds a canonical representative for each element of
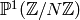 . Given an arbitrary
. Given an arbitrary
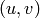 , we first find the canonical equivalent elements
, we first find the canonical equivalent elements 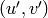 .
If
.
If 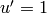 , then the index is
, then the index is 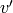 . If
. If
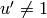 , we find the corresponding element
in an explicit sorted list, e.g., using binary search.
, we find the corresponding element
in an explicit sorted list, e.g., using binary search.
In the following algorithm, 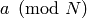 denotes the residue of
denotes the residue of  modulo
modulo  that satisfies
that satisfies 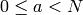 .
Note that we never create and store the
list (13) itself in memory.
.
Note that we never create and store the
list (13) itself in memory.
Algorithm 1.50
Given 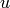 and
and  and a positive integer
and a positive integer  ,
this algorithm outputs
a pair
,
this algorithm outputs
a pair 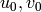 such that
such that 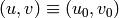 as
elements of
as
elements of 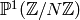 and
and 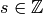 such that
such that 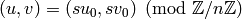 .
Moreover, the element
.
Moreover, the element 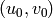 does not
depend on the class of
does not
depend on the class of 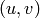 , i.e., for any
, i.e., for any  with
with 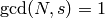 the input
the input 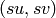 also outputs
also outputs 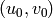 .
If
.
If 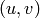 is not in
is not in 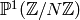 , this algorithm
outputs
, this algorithm
outputs 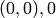 .
.
- [Reduce] Reduce both
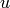 and
and  modulo
modulo  .
. - [Easy
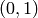 Case] If
Case] If 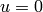 , check that
, check that 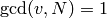 .
If so, return
.
If so, return 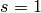 and
and 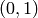 ; otherwise return
; otherwise return  .
. - [GCD] Compute
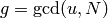 and
and 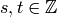 such that
such that 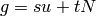 .
. - [Not in
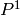 ?] We have
?] We have 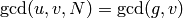 , so if
, so if
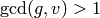 , then
, then 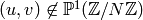 ,
and we return
,
and we return  .
. - [Pseudo-Inverse]
Now
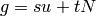 , so we may think of
, so we may think of  as “pseudo-inverse”
of
as “pseudo-inverse”
of 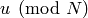 , in the sense that
, in the sense that 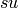 is as close as possible to
being
is as close as possible to
being  modulo
modulo  . Note that since
. Note that since 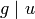 , changing
, changing  modulo
modulo
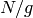 does not change
does not change 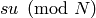 . We can adjust
. We can adjust  modulo
modulo 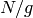 so it is coprime to
so it is coprime to  (by adding multiples of
(by adding multiples of
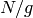 to
to  ). (This is because
). (This is because 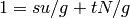 , so
, so
 is a unit mod
is a unit mod 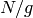 , and the map
, and the map 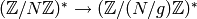 is surjective, e.g., as we saw in the proof of
Algorithm 4.28.)
is surjective, e.g., as we saw in the proof of
Algorithm 4.28.) - [Multiply by
 ] Multiply
] Multiply 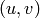 by
by  , and replace
, and replace
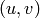 by the
equivalent element
by the
equivalent element 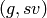 of
of  .
. - [Normalize]
Compute the unique pair
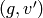 equivalent to
equivalent to 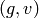 that
minimizes
that
minimizes  , as follows:
, as follows:- [Easy Case] If
 , this pair is
, this pair is  .
. - [Enumerate and Find Best]
Otherwise, note that if
 and
and
 , then
, then 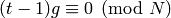 , so
, so 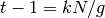 for some
for some  with
with 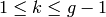 . Then for
. Then for 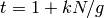 coprime to
coprime to  ,
we have
,
we have 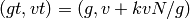 . So we compute
all pairs
. So we compute
all pairs 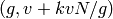 and pick out the one that minimizes the
least nonnegative residue of
and pick out the one that minimizes the
least nonnegative residue of 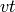 modulo
modulo  .
. - [Invert
 and Output]
The
and Output]
The  that we computed in the above steps multiplies
the input
that we computed in the above steps multiplies
the input 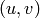 to give the output
to give the output  . Thus we
invert it, since the scalar we output
multiplies
. Thus we
invert it, since the scalar we output
multiplies  to give
to give  .
.
- [Easy Case] If
Remark 1.51
In the above algorithm, there are many gcd’s with  so one should
create a table of the gcd’s of
so one should
create a table of the gcd’s of  with
with  .
.
Remark 1.52
Another approach is to instead use that
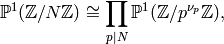
where 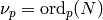 ,
and that it is relatively easy to enumerate the
elements of
,
and that it is relatively easy to enumerate the
elements of 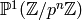 for a prime power
for a prime power 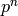 .
.
Algorithm 1.53
Given an integer  , this algorithm makes a sorted list of the
distinct representatives
, this algorithm makes a sorted list of the
distinct representatives  of
of  with
with
 , as output by Algorithm 1.50.
, as output by Algorithm 1.50.
- For each
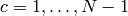 with
with 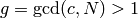 do the
following:
do the
following:- Use Algorithm 1.50 to compute
the canonical representative
 equivalent to
equivalent to  ,
and include it in the list.
,
and include it in the list. - If
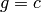 , for each
, for each 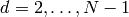 with
with 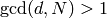 and
and 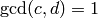 , append the normalized representative
of
, append the normalized representative
of  to the list.
to the list.
- Use Algorithm 1.50 to compute
the canonical representative
- Sort the list.
- Pass through the sorted list and delete any duplicates.
Explicit Examples¶
Explicit detailed examples are crucial when implementing modular symbols algorithms from scratch. This section contains a number of such examples.
Examples of Computation of 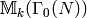 ¶
¶
In this section, we compute 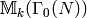 explicitly in a few cases.
explicitly in a few cases.
Example 1.54
We compute 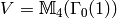 . Because
. Because 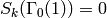 and
and 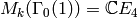 , we expect
, we expect  to have dimension
to have dimension  and for each integer
and for each integer  the Hecke operator
the Hecke operator  to have eigenvalue the
sum
to have eigenvalue the
sum 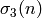 of the cubes of positive divisors of
of the cubes of positive divisors of  .
.
The Manin symbols are
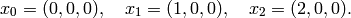
The relation matrix is
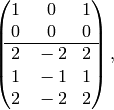
where the first two rows correspond to  -relations and the second
three to
-relations and the second
three to  -relations.
Note that we do not include all
-relations.
Note that we do not include all  -relations, since it is obvious
that some are redundant, e.g.,
-relations, since it is obvious
that some are redundant, e.g., 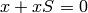 and
and 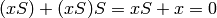 are the same since
are the same since  has order
has order  .
.
The echelon form of the relation matrix is
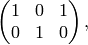
where we have deleted the zero rows from the bottom. Thus we may replace the above complicated list of relations with the following simpler list of relations:
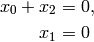
from which we immediately read off that the second generator 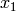 is
is
 and
and 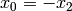 . Thus
. Thus 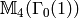 has dimension
has dimension  , with
basis the equivalence class of
, with
basis the equivalence class of 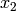 (or of
(or of 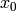 ).
).
Next we compute the Hecke operator  on
on  .
The Heilbronn matrices
of determinant
.
The Heilbronn matrices
of determinant  from Proposition 1.29
are
from Proposition 1.29
are
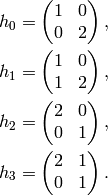
To compute  , we apply each of these matrices to
, we apply each of these matrices to 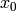 ,
then reduce modulo the relations.
We have
,
then reduce modulo the relations.
We have
![x_2\mtwo{1}{0}{0}{2} &= [X^2,(0,0)] \mtwo{1}{0}{0}{2}
x_2,\\
x_2 \mtwo{1}{0}{1}{2} &= [X^2,(0,0)] = x_2,\\
x_2 \mtwo{2}{0}{0}{1} &= [(2X)^2,(0,0)] = 4x_2,\\
x_2 \mtwo{2}{1}{0}{1} &= [(2X+1)^2,(0,0)] = x_0 + 4x_1 + 4x_2
\sim 3x_2.](_images/math/85819d95e89c3c4432b878e054e14036ee482fcd.png)
Summing we see that 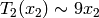 in
in 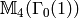 .
Notice that
.
Notice that
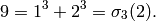
The Heilbronn matrices of determinant  from
Proposition 1.29 are
from
Proposition 1.29 are
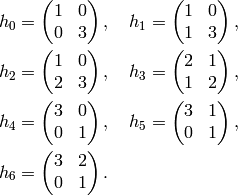
We have
![x_2 \mtwo{1}{0}{0}{3} &= [X^2,(0,0)] \mtwo{1}{0}{0}{3} =
x_2,\\
x_2 \mtwo{1}{0}{1}{3} &= [X^2,(0,0)] = x_2,\\
x_2 \mtwo{1}{0}{2}{3} &= [X^2,(0,0)] = x_2,\\
x_2 \mtwo{2}{1}{2}{2} &= [(2X+1)^2,(0,0)] = x_0 + 4x_1 + 4x_2
\sim 3x_2,\\
x_2 \mtwo{3}{0}{0}{1} &= [(3X)^2,(0,0)] = 9x_2,\\
x_2 \mtwo{3}{1}{0}{1} &= [(3X+1)^2,(0,0)] = x_0 + 6x_1 + 9x_2 \sim 8x_2,\\
x_2 \mtwo{3}{2}{0}{1} &= [(3X+2)^2,(0,0)] = 4x_0 + 12x_1 + 9x_2 \sim 5x_2.\\](_images/math/9da02b509402fcdc72a38cede41ccf4b3e0e933e.png)
Summing we see that
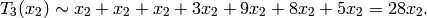
Notice that
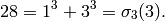
Example 1.55
Next we compute  explicitly.
The Manin symbol generators are
explicitly.
The Manin symbol generators are
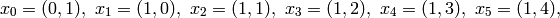
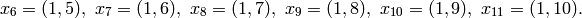
The relation matrix is as follows, where the  -relations
are above the line and the
-relations
are above the line and the  -relations
are below it:
-relations
are below it:

In weight  , two out of three
, two out of three  -relations are redundant, so we
do not include them.
The reduced row echelon form of the relation matrix is
-relations are redundant, so we
do not include them.
The reduced row echelon form of the relation matrix is
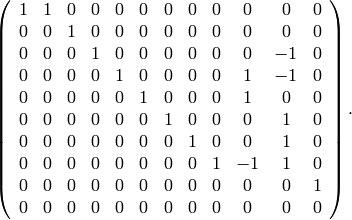
From the echelon form we see that every symbol
is equivalent to a combination of
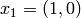 ,
, 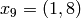 , and
, and  .
(Notice that columns
.
(Notice that columns  ,
,  , and
, and  are the pivot
columns, where we index columns starting at
are the pivot
columns, where we index columns starting at  .)
.)
To compute  , we apply each of the Heilbronn
matrices of determinant
, we apply each of the Heilbronn
matrices of determinant  from Proposition 1.29
to
from Proposition 1.29
to 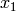 , then to
, then to 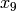 , and finally to
, and finally to 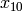 .
The matrices are as in Example 1.54 above.
We have
.
The matrices are as in Example 1.54 above.
We have
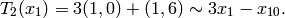
Applying  to
to 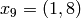 , we get
, we get
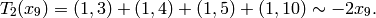
Applying  to
to 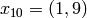 , we get
, we get
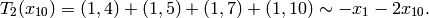
Thus the matrix of  with respect to this basis is
with respect to this basis is
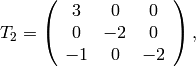
where we write the matrix as an operator on the left on vectors
written in terms of  ,
,  , and
, and  .
The matrix
.
The matrix  has characteristic polynomial
has characteristic polynomial
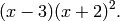
The 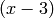 factor corresponds to the weight
factor corresponds to the weight  Eisenstein
series, and the
Eisenstein
series, and the 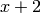 factor corresponds to the elliptic
curve
factor corresponds to the elliptic
curve  , which has
, which has
Example 1.56
In this example, we compute  ,
which illustrates both weight greater than
,
which illustrates both weight greater than  and level greater than
and level greater than  .
We have the following generating Manin symbols:
.
We have the following generating Manin symbols:
![x_{0} &= [XY^4,(0,1)],\qquad x_{1} = [XY^4,(1,0)],\\
x_{2} &= [XY^4,(1,1)], \qquad x_{3} = [XY^4,(1,2)],\\
x_{4} &= [XY^3,(0,1)], \qquad x_{5} = [XY^3,(1,0)],\\
x_{6} &= [XY^3,(1,1)], \qquad
x_{7} = [XY^3,(1,2)],\\
x_{8} &= [X^2Y^2,(0,1)], \qquad
\!\!x_{9} = [X^2Y^2,(1,0)],\\
x_{10} &= [X^2Y^2,(1,1)], \qquad
\!\!\!\!x_{11} = [X^2Y^2,(1,2)],\\
x_{12} &= [X^3Y,(0,1)], \qquad
x_{13} = [X^3Y,(1,0)],\\
x_{14} &= [X^3Y,(1,1)], \qquad
x_{15} = [X^3Y,(1,2)],\\
x_{16} &= [X^4Y,(0,1)], \qquad
x_{17} = [X^4Y,(1,0)],\\
x_{18} &= [X^4Y,(1,1)], \qquad
x_{19} = [X^4Y,(1,2)].\\](_images/math/c23c748c064afa76e3d39429a3f1d1ebe1719542.png)
The relation matrix is already very large
for  . It is as follows, where the
. It is as follows, where the  -relations
are before the line and the
-relations
are before the line and the  -relations after it:
-relations after it:
The reduced row echelon form of the relations matrix, with zero rows removed is

Since these relations are equivalent to the original
relations, we see how
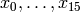 can be expressed in
terms of
can be expressed in
terms of 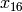 ,
, 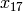 ,
, 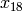 , and
, and 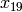 .
Thus
.
Thus 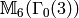 has dimension
has dimension 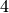 .
For example,
.
For example,
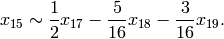
Notice that the number of relations is already quite large. It is
perhaps surprising how complicated the presentation is already for
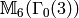 . Because there are denominators in the
relations, the above calculation is only a computation of
. Because there are denominators in the
relations, the above calculation is only a computation of
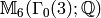 . Computing
. Computing 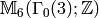 involves
finding a
involves
finding a 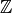 -basis for the kernel of the relation matrix
(see Exercise 7.5).
-basis for the kernel of the relation matrix
(see Exercise 7.5).
As before, we find that with respect to the basis
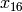 ,
, 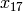 ,
, 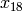 , and
, and 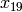

Notice that there are denominators in the matrix for
 with respect to this basis. It is clear from
the definition of
with respect to this basis. It is clear from
the definition of  acting on Manin symbols that
acting on Manin symbols that
 preserves the
preserves the  -module
-module 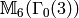 ,
so there is some basis for
,
so there is some basis for 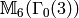 such that
such that  is given by an integer matrix. Thus
the characteristic polynomial
is given by an integer matrix. Thus
the characteristic polynomial  of
of  will have integer
coefficients; indeed,
will have integer
coefficients; indeed,
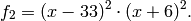
Note the factor 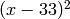 , which comes from the two images
of the Eisenstein series
, which comes from the two images
of the Eisenstein series  of level
of level  . The
factor
. The
factor 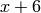 comes from the cusp form
comes from the cusp form
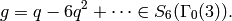
By computing more Hecke operators  , we
can find more coefficients of
, we
can find more coefficients of  .
For example, the charpoly of
.
For example, the charpoly of  is
is
 , and the matrix of
, and the matrix of  is
is
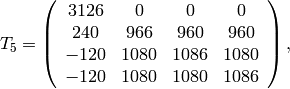
which has characteristic polynomial
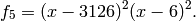
The matrix of  is
is
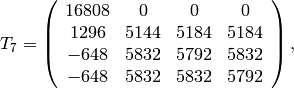
with characteristic polynomial
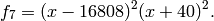
One can put this information together to deduce that
Example 1.57
Consider  , which has dimension
, which has dimension  .
With respect to the symbols
.
With respect to the symbols
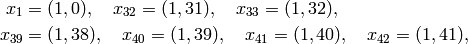
the matrix of  is
is
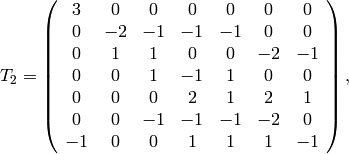
which has characteristic polynomial
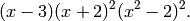
There is one Eisenstein series and there are three cusp forms
with 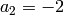 and
and 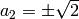 .
.
Example 1.58
To compute
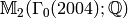 , we first make
a list of the
, we first make
a list of the
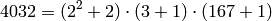
elements 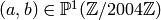 using Algorithm 1.50.
The list looks like this:
using Algorithm 1.50.
The list looks like this:
For each of the symbols  , we consider the
, we consider the  -relations
and
-relations
and  -relations.
Ignoring the redundant relations, we find
-relations.
Ignoring the redundant relations, we find 
 -relations and
-relations and
 -relations. It is simple to quotient out by the
-relations. It is simple to quotient out by the
 -relations, e.g., by identifying
-relations, e.g., by identifying 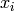 with
with 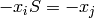 for
some
for
some 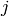 (or setting
(or setting 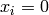 if
if 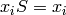 ). Once we have taken
the quotient by the
). Once we have taken
the quotient by the  -relations, we take the image of all
-relations, we take the image of all
 of the
of the  -relations modulo the
-relations modulo the  -relations and quotient out by
those relations. Because
-relations and quotient out by
those relations. Because  and
and  do not commutate, we cannot
only quotient out by
do not commutate, we cannot
only quotient out by  -relations
-relations 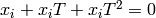 where
the
where
the 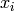 are the basis after quotienting out by the
are the basis after quotienting out by the  -relations.
The relation matrix has rank
-relations.
The relation matrix has rank 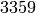 , so
, so 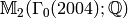 has
dimension
has
dimension  .
.
If we instead compute the quotient  of
of 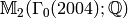 by the subspace of elements
by the subspace of elements 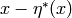 ,
we include relations
,
we include relations 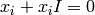 , where
, where 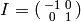 .
There are now 2016
.
There are now 2016  -relations, 2024
-relations, 2024 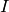 -relations,
and 1344
-relations,
and 1344  -relations. Again, it is relatively easy to quotient
out by the
-relations. Again, it is relatively easy to quotient
out by the  -relations by identifying
-relations by identifying 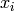 and
and 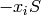 .
We then take the image of all
.
We then take the image of all 
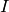 -relations modulo the
-relations modulo the
 -relations, and again directly quotient out by the
-relations, and again directly quotient out by the 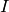 -relations
by identifying
-relations
by identifying ![[x_i]](_images/math/487e544a359d32cf1d604be8c662ffb928535bd1.png) with
with ![-[x_iI]=-[x_j]](_images/math/0db15655aa8691e5c33046015df3730d3a4a76fe.png) for some
for some  , where
by
, where
by ![[x_i]](_images/math/487e544a359d32cf1d604be8c662ffb928535bd1.png) we mean the class of
we mean the class of 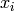 modulo the
modulo the  -relations.
Finally, we quotient out by the
-relations.
Finally, we quotient out by the 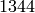
 -relations, which involves
sparse Gauss elimination on a matrix with
-relations, which involves
sparse Gauss elimination on a matrix with 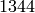 rows
and at most three nonzero entries per row.
The dimension of
rows
and at most three nonzero entries per row.
The dimension of 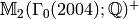 is
is 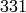 .
.
Refined Algorithm for the Presentation¶
Algorithm 1.59
This is an algorithm to compute 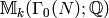 or
or
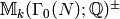 , which
only requires doing generic sparse linear algebra to deal
with the three term
, which
only requires doing generic sparse linear algebra to deal
with the three term  -relations.
-relations.
Let
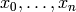 by a list of all Manin symbols.
by a list of all Manin symbols.Quotient out the two-term
 -relations and if the
-relations and if the  quotient is desired, by the two-term
quotient is desired, by the two-term 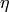 -relations.
(Note that this is more subtle than
just “identifying symbols in pairs”,
since complicated relations can cause generators to surprisingly
equal
-relations.
(Note that this is more subtle than
just “identifying symbols in pairs”,
since complicated relations can cause generators to surprisingly
equal  .)
Let
.)
Let ![[x_i]](_images/math/487e544a359d32cf1d604be8c662ffb928535bd1.png) denote the class of
denote the class of 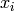 after this quotienting
process.
after this quotienting
process.Create a sparse matrix
 with
with  columns, whose rows
encode the relations
columns, whose rows
encode the relations![[x_i] + [x_iT] + [x_iT^2] = 0.](_images/math/f05aefe6b28554d38ddb235662923d34e8667ff7.png)
For example, there are about
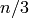 such rows when
such rows when
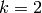 .
The number of nonzero entries per row is at most
.
The number of nonzero entries per row is at most 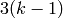 .
Note that we must include rows for all
.
Note that we must include rows for all  , since
even if
, since
even if ![[x_i] = [x_j]](_images/math/c0a83ea46386d0ca4de420a7027e6e01c33c1e7d.png) , it need not be the case that
, it need not be the case that
![[x_i T] = [x_jT]](_images/math/55465c71c6bbd80a9d32d036ebde7f2d2fbd7ef5.png) , since the matrices
, since the matrices  and
and  do not commute.
However, we have an a priori formula for the dimension
of the quotient by all these relations, so we could omit
many relations and just check that there are enough at the
end—if there are not, we add in more.
do not commute.
However, we have an a priori formula for the dimension
of the quotient by all these relations, so we could omit
many relations and just check that there are enough at the
end—if there are not, we add in more.Compute the reduced row echelon form of
 using
Algorithm 7.6. For
using
Algorithm 7.6. For 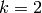 , this is the echelon
form of a matrix with size about
, this is the echelon
form of a matrix with size about 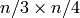 .
.Use what we have done above to read off a sparse matrix
 that expresses each of the
that expresses each of the  Manin symbols in terms of
a basis of Manin symbols, modulo the relations.
Manin symbols in terms of
a basis of Manin symbols, modulo the relations.
Applications¶
Later in This Book¶
We sketch some of the ways in which we will apply the modular symbols algorithms of this chapter later in this book.
Cuspidal modular symbols are in Hecke-equivariant duality with
cuspidal modular forms, and as such we can compute modular forms by
computing systems of eigenvalues for the Hecke operators acting on
modular symbols. By the Atkin-Lehner-Li theory of newforms (see,
e.g., Theorem 9.4), we can construct 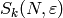 for
any
for
any  , any
, any  , and
, and 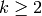 using this method. See
Chapter Modular Forms for more details.
using this method. See
Chapter Modular Forms for more details.
Once we can compute spaces of modular symbols, we move to computing
the corresponding modular forms. We
define inclusion and trace maps from modular symbols of one level  to modular symbols of level a multiple or divisor of
to modular symbols of level a multiple or divisor of  . Using these,
we compute the quotient
. Using these,
we compute the quotient  of the new subspace of cuspidal modular
symbols on which a “star involution” acts as
of the new subspace of cuspidal modular
symbols on which a “star involution” acts as 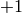 . The Hecke
operators act by diagonalizable commuting matrices on this space, and
computing the systems of Hecke eigenvalues is equivalent
to computing newforms
. The Hecke
operators act by diagonalizable commuting matrices on this space, and
computing the systems of Hecke eigenvalues is equivalent
to computing newforms 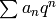 . In this way, we
obtain a list of all newforms (normalized eigenforms) in
. In this way, we
obtain a list of all newforms (normalized eigenforms) in
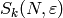 for any
for any  ,
,  , and
, and 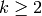 .
.
In Chapter Computing Periods, we compute with the period mapping from
modular symbols to  attached to a newform
attached to a newform 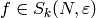 .
When
.
When 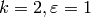 and
and  has rational Fourier coefficients, this
gives a method to compute the period lattice associated to a modular
elliptic curve attached to a newform (see
Section All Elliptic Curves of Given Conductor). In general, computation of this map
is important when finding equations for modular
has rational Fourier coefficients, this
gives a method to compute the period lattice associated to a modular
elliptic curve attached to a newform (see
Section All Elliptic Curves of Given Conductor). In general, computation of this map
is important when finding equations for modular  -curves, CM
curves, and curves with a given modular Jacobian. It is also
important for computing special values of the
-curves, CM
curves, and curves with a given modular Jacobian. It is also
important for computing special values of the  -function
-function 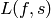 at
integer points in the critical strip.
at
integer points in the critical strip.
Discussion of the Literature and Research¶
Modular symbols were introduced by Birch [Bir71] for
computations in support of the Birch and Swinnerton-Dyer conjecture.
Manin [Man72] used modular symbols to
prove rationality results about special values of  -functions.
-functions.
Merel’s paper [Mer94] builds on work of Shokurov (mainly
[Sho80a]), which develops a higher-weight
generalization of Manin’s work partly to understand rationality
properties of special values of  -functions. Cremona’s book
[Cre97a] discusses how to compute the space of
weight
-functions. Cremona’s book
[Cre97a] discusses how to compute the space of
weight  modular symbols for
modular symbols for  , in connection with the
problem of enumerating all elliptic curves of given conductor, and his
article [Cre92] discusses the
, in connection with the
problem of enumerating all elliptic curves of given conductor, and his
article [Cre92] discusses the  case and
computation of modular symbols with character.
case and
computation of modular symbols with character.
There have been several Ph.D. theses about modular symbols.
Basmaji’s thesis [Bas96] contains tricks to efficiently
compute Hecke operators  , with
, with  very large (see
Section Basmaji’s Trick), and also discusses how to compute spaces
of half integral weight modular forms building on what one can get
from modular symbols of integral weight. The author’s Ph.D. thesis
[Ste00] discusses higher-weight modular
symbols and applies modular symbols to study Shafarevich-Tate groups
(see also [Aga00]). Martin’s thesis [Mar01] is
about an attempt to study an analogue of analytic modular symbols for
weight
very large (see
Section Basmaji’s Trick), and also discusses how to compute spaces
of half integral weight modular forms building on what one can get
from modular symbols of integral weight. The author’s Ph.D. thesis
[Ste00] discusses higher-weight modular
symbols and applies modular symbols to study Shafarevich-Tate groups
(see also [Aga00]). Martin’s thesis [Mar01] is
about an attempt to study an analogue of analytic modular symbols for
weight  . Gabor Wiese’s thesis [Wie05] uses modular
symbols methods to study weight 1 modular forms modulo
. Gabor Wiese’s thesis [Wie05] uses modular
symbols methods to study weight 1 modular forms modulo  . Lemelin’s
thesis [Lem01] discusses modular symbols for quadratic
imaginary fields in the context of
. Lemelin’s
thesis [Lem01] discusses modular symbols for quadratic
imaginary fields in the context of  -adic analogues of the Birch and
Swinnerton-Dyer conjecture. See also the survey paper
[FM99], which discusses computation with weight
-adic analogues of the Birch and
Swinnerton-Dyer conjecture. See also the survey paper
[FM99], which discusses computation with weight  modular symbols in the context of modular abelian
varieties.
modular symbols in the context of modular abelian
varieties.
The appendix of this book is about
analogues of modular symbols for groups besides
finite index subgroups of  , e.g., for subgroup
of higher rank groups such as
, e.g., for subgroup
of higher rank groups such as 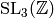 .
There has also been work on computing Hilbert
modular forms, e.g., by Lassina Dembel’e [Dem05] Hilbert modular forms are functions on a product of copies of
.
There has also been work on computing Hilbert
modular forms, e.g., by Lassina Dembel’e [Dem05] Hilbert modular forms are functions on a product of copies of  , and
, and
 is replaced by a group of matrices with entries in a
totally real field.
is replaced by a group of matrices with entries in a
totally real field.
Glenn Stevens, Robert Pollack and Henri Darmon (see
[DP04]) have worked for many years to develop an
analogue of modular symbols in a rigid analytic context, which is
helpful for questions about computing with overconvergent
 -adic modular forms or proving results about
-adic modular forms or proving results about  -adic
-adic
 -functions.
-functions.
Finally we mention that Barry Mazur and some other authors
use the term “modular symbol”
in a different way than we do.
They use the term in a way that is dual
to our usage; for example, they attach a “modular symbol” to
a modular form or elliptic curve.
See [MTT86] for an extensive discussion
of modular symbols from this point of view, where they are used to
construct  -adic
-adic  -functions.
-functions.
Exercises¶
Exercise 1.11
Suppose  is an integer multiple of
is an integer multiple of  . Prove
that the natural map
. Prove
that the natural map 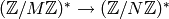 is surjective.
is surjective.
Exercise 1.12
Prove that 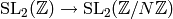 is surjective
(see Lemma 1.36).
is surjective
(see Lemma 1.36).
Exercise 1.13
Compute 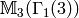 . List
each Manin symbol the relations they satisfy, compute
the quotient, etc. Find the matrix of
. List
each Manin symbol the relations they satisfy, compute
the quotient, etc. Find the matrix of  .
(Check: The dimension of
.
(Check: The dimension of 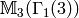 is
is  , and
the characteristic polynomial of
, and
the characteristic polynomial of  is
is 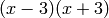 .)
.)
Exercise 1.14
Finish the proof of Proposition 1.38.
Exercise 1.15
- Show that if
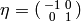 , then
, then
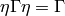 for
for 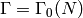 and
and 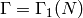 .
. - (*) Give an example of a finite index
subgroup
 such that
such that 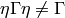 .
.