Modular Forms of Level 1¶
In this chapter we study in detail the structure of level  modular
forms, i.e., modular forms on
modular
forms, i.e., modular forms on 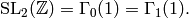 We assume some complex analysis (e.g., the residue theorem),
linear algebra, and that the reader has
read Chapter Modular Forms.
We assume some complex analysis (e.g., the residue theorem),
linear algebra, and that the reader has
read Chapter Modular Forms.
Examples of Modular Forms of Level 1¶
In this section we will finally see some examples of modular forms of
level  ! We first introduce the Eisenstein series and
then define
! We first introduce the Eisenstein series and
then define  , which is a cusp form of weight
, which is a cusp form of weight 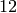 . In
Section Structure Theorem for Level 1 Modular Forms we prove the structure theorem,
which says that all modular forms of level
. In
Section Structure Theorem for Level 1 Modular Forms we prove the structure theorem,
which says that all modular forms of level  are polynomials
in Eisenstein series.
are polynomials
in Eisenstein series.
For an even integer 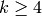 , the
nonnormalized weight
, the
nonnormalized weight  Eisenstein series is the
function on the extended upper half plane
Eisenstein series is the
function on the extended upper half plane
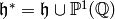 given by
given by
(1)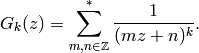
The star on top of the sum symbol means that
for each  the sum is over all
the sum is over all 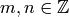 such that
such that
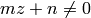 .
.
Proposition 2.1
The function 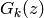 is a modular form of weight
is a modular form of weight  , i.e.,
, i.e.,
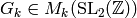 .
.
Proof
See [Ser73, Section VII.2.3] for a proof
that 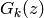 defines a holomorphic function on
defines a holomorphic function on 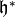 .
To see that
.
To see that 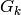 is modular, observe that
is modular, observe that
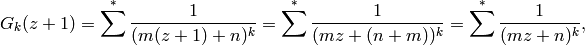
where for the last equality we use that the map
 on
on  is invertible.
Also,
is invertible.
Also,
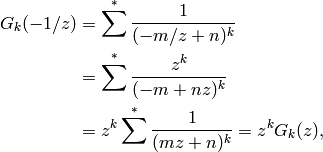
where we use that 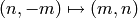 is invertible.
is invertible.
Proposition 2.2
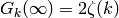 , where
, where 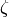 is the Riemann zeta
function.
is the Riemann zeta
function.
Proof
As 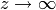 (along the imaginary axis) in (1),
the terms that involve
(along the imaginary axis) in (1),
the terms that involve  with
with 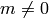 go to
go to  .
Thus
.
Thus
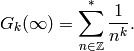
This sum is twice 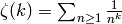 ,
as claimed.
,
as claimed.
The Cusp Form  ¶
¶
Suppose 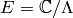 is an elliptic curve over
is an elliptic curve over  , viewed as a
quotient of
, viewed as a
quotient of  by a lattice
by a lattice 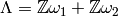 , with
, with
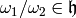 (see [DS05, Section 1.4]).
The Weierstrass
(see [DS05, Section 1.4]).
The Weierstrass 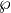 -function of
the lattice
-function of
the lattice 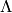 is
is
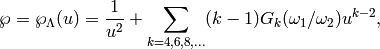
where the sum is over even integers 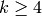 .
It satisfies the differential equation
.
It satisfies the differential equation
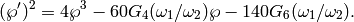
If we set 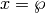 and
and 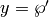 , the above is an (affine) equation of
the form
, the above is an (affine) equation of
the form 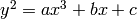 for an elliptic curve that is complex
analytically isomorphic to
for an elliptic curve that is complex
analytically isomorphic to 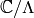 (see [Ahl78, pg. 277]
for why the cubic has distinct roots).
(see [Ahl78, pg. 277]
for why the cubic has distinct roots).
The discriminant of the cubic
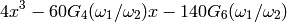
is 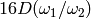 , where
, where
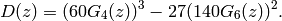
Since 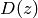 is the difference of two modular forms of
weight
is the difference of two modular forms of
weight 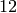 it has weight
it has weight 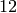 . Morever,
. Morever,
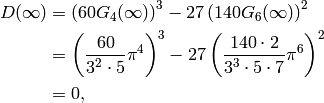
so  is a cusp form of weight
is a cusp form of weight 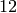 .
.
Let
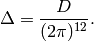
Lemma 2.3
If 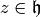 , then
, then 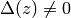 .
.
Proof
Let 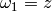 and
and 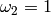 .
Since
.
Since 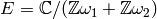 is an elliptic curve,
it has nonzero discriminant
is an elliptic curve,
it has nonzero discriminant
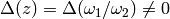 .
.
Proposition 2.4
We have 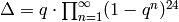 .
.
Proof
See [Ser73, Thm. 6, pg. 95].
Remark 2.5
Sage computes the  -expansion of
-expansion of  efficiently
to high precision using the command delta_qexp:
efficiently
to high precision using the command delta_qexp:
sage: delta_qexp(6)
q - 24*q^2 + 252*q^3 - 1472*q^4 + 4830*q^5 + O(q^6)
Fourier Expansions of Eisenstein Series¶
Recall from (?) that elements  of
of 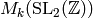 can be
expressed as formal power series in terms of
can be
expressed as formal power series in terms of 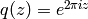 and
that this expansion is called the Fourier expansion of
and
that this expansion is called the Fourier expansion of  .
The following proposition gives the Fourier expansion of the
Eisenstein series
.
The following proposition gives the Fourier expansion of the
Eisenstein series 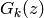 .
.
Definition 2.6
For any integer 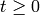 and any positive integer
and any positive integer  ,
the sigma function
,
the sigma function

is the sum of the 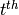 powers of the positive divisors of
powers of the positive divisors of  .
Also, let
.
Also, let 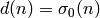 , which is the number
of divisors of
, which is the number
of divisors of  , and let
, and let 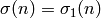 .
For example, if
.
For example, if  is prime, then
is prime, then 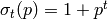 .
.
Proposition 2.7
For every even integer 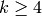 , we have
, we have

Proof
See [Ser73, Section VII.4], which uses clever manipulations of series, starting with the identity
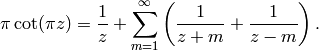
From a computational point of view, the  -expansion of
Proposition 2.7 is unsatisfactory because it involves
transcendental numbers. To understand these numbers, we introduce the
Bernoulli numbers
-expansion of
Proposition 2.7 is unsatisfactory because it involves
transcendental numbers. To understand these numbers, we introduce the
Bernoulli numbers 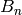 for
for 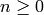 defined by the
following equality of formal power series:
defined by the
following equality of formal power series:
(2)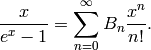
Expanding the power series, we have
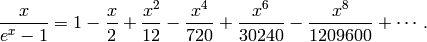
As this expansion suggests, the Bernoulli numbers 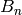 with
with 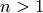 odd
are
odd
are  (see Exercise 2.2). Expanding the series further,
we obtain the following table:
(see Exercise 2.2). Expanding the series further,
we obtain the following table:
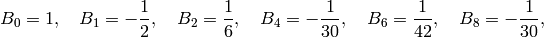
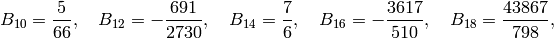
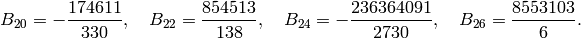
See Section Fast Computation of Bernoulli Numbers for a discussion of fast (analytic) methods for computing Bernoulli numbers.
We compute some Bernoulli numbers in Sage:
sage: bernoulli(12)
-691/2730
sage: bernoulli(50)
495057205241079648212477525/66
sage: len(str(bernoulli(10000)))
27706
A key fact is that Bernoulli numbers are
rational numbers and they are connected to values of 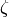 at
positive even integers.
at
positive even integers.
Proposition 2.8
If 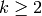 is an even integer, then
is an even integer, then
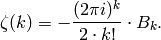
Proof
This is proved
by manipulating a series expansion of 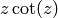 (see [Ser73, Section VII.4]).
(see [Ser73, Section VII.4]).
Definition 2.9
The normalized Eisenstein series of even weight 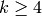 is
is
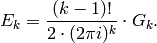
Combining Proposition 2.7 and Proposition 2.8, we see that
(3)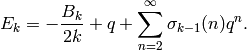
Warning
Our series 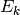 is normalized so that the coefficient of
is normalized so that the coefficient of  is
is  , but often in the literature
, but often in the literature 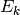 is normalized so that the
constant coefficient is
is normalized so that the
constant coefficient is  . We use the normalization with the
coefficient of
. We use the normalization with the
coefficient of  equal to
equal to  , because then the eigenvalue of the
, because then the eigenvalue of the
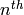 Hecke operator (see Section Hecke Operators) is the
coefficient of
Hecke operator (see Section Hecke Operators) is the
coefficient of 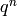 . Our normalization is also convenient when
considering congruences between cusp forms and Eisenstein series.
. Our normalization is also convenient when
considering congruences between cusp forms and Eisenstein series.
Structure Theorem for Level 1 Modular Forms¶
In this section we describe a structure theorem for modular
forms of level  .
If
.
If  is a nonzero meromorphic function on
is a nonzero meromorphic function on  and
and 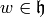 , let
, let
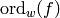 be the largest integer
be the largest integer  such that
such that 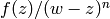 is
holomorphic at
is
holomorphic at 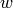 . If
. If 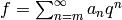 with
with
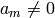 , we set
, we set 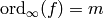 . We will use the following
theorem to give a presentation for the vector space of modular forms
of weight
. We will use the following
theorem to give a presentation for the vector space of modular forms
of weight  ; this presentation yields an algorithm
to compute this space.
; this presentation yields an algorithm
to compute this space.
Let 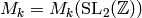 denote the complex vector space of modular
forms of weight
denote the complex vector space of modular
forms of weight  for
for  . The
standard fundamental domain
. The
standard fundamental domain 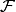 for
for  is the set of
is the set of 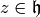 with
with 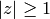 and
and 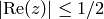 . Let
. Let
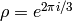 .
.
Theorem 2.11
Let  be any integer and
suppose
be any integer and
suppose 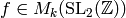 is nonzero. Then
is nonzero. Then
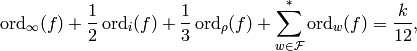
where 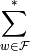 is the sum over elements of
is the sum over elements of 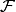 other than
other than  and
and 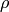 !.
!.
Proof
The proof in [Ser73, Section VII.3] uses the residue theorem.
Let 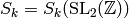 index{
index{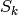 }
denote the subspace of weight
}
denote the subspace of weight  cusp forms for
cusp forms for  . We have
an exact sequence
. We have
an exact sequence
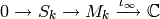
that sends 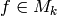 to
to 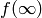 . When
. When 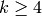 is even, the
space
is even, the
space 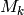 contains the Eisenstein series
contains the Eisenstein series 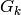 , and
, and
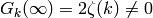 , so the map
, so the map 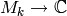 is surjective.
This proves the following lemma.
is surjective.
This proves the following lemma.
Lemma 2.12
If 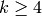 is even, then
is even, then 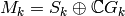 and the following sequence is exact:
and the following sequence is exact:
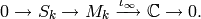
Proposition 2.13
For 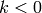 and
and 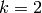 , we have
, we have 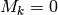 .
.
Proof
Suppose 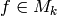 is nonzero yet
is nonzero yet 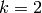 or
or 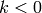 . By
Theorem 2.11,
. By
Theorem 2.11,
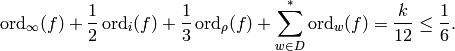
This is not possible because each quantity on the left is nonnegative so
whatever the sum is, it is too big (or  , in which case
, in which case 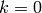 ).
).
Theorem 2.14
Multiplication by  defines an isomorphism
defines an isomorphism 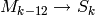 .
.
Proof
By Lemma 2.3,  is not identically
is not identically  , so
because
, so
because  is holomorphic, multiplication
by
is holomorphic, multiplication
by  defines an injective map
defines an injective map 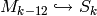 .
To see that this map is surjective, we show that if
.
To see that this map is surjective, we show that if 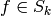 , then
, then
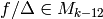 .
Since
.
Since  has weight
has weight 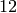 and
and 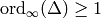 ,
Theorem 2.11 implies that
,
Theorem 2.11 implies that  has a simple
zero at
has a simple
zero at  and does not vanish on
and does not vanish on  .
Thus if
.
Thus if 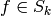 and if we let
and if we let 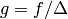 , then
, then  is holomorphic
and satisfies the appropriate transformation formula, so
is holomorphic
and satisfies the appropriate transformation formula, so 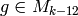 .
.
Corollary 2.15
For 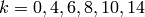 , the space
, the space 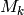 has dimension
has dimension  , with
basis
, with
basis  ,
, 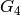 ,
, 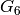 ,
, 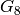 ,
, 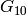 , and
, and 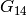 , respectively, and
, respectively, and
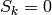 .
.
Proof
Combining Proposition 2.13 with
Theorem 2.14, we see that the spaces 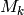 for
for
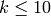 cannot have dimension greater than
cannot have dimension greater than  , since otherwise
, since otherwise
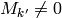 for some
for some 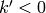 . Also
. Also 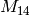 has dimension at most
has dimension at most  , since
, since
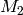 has dimension
has dimension  . Each of the indicated spaces of weight
. Each of the indicated spaces of weight
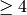 contains the indicated Eisenstein series and so has
dimension
contains the indicated Eisenstein series and so has
dimension  , as claimed.
, as claimed.
Corollary 2.16
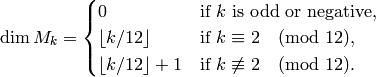
Here 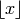 is the biggest integer
is the biggest integer 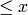 .
.
Proof
As we have already seen above, the formula is true when 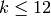 .
By Theorem 2.14, the dimension increases by
.
By Theorem 2.14, the dimension increases by  when
when  is replaced by
is replaced by 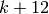 .
.
Theorem 2.17
The space 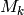 has as basis the modular forms
has as basis the modular forms 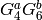 , where
, where
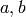 run over all pairs of nonnegative integers such that
run over all pairs of nonnegative integers such that
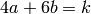 .
.
Proof
Fix an even integer  . We first prove by induction that the
modular forms
. We first prove by induction that the
modular forms 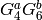 generate
generate 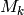 ; the cases
; the cases 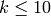 and
and
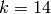 follow from the above arguments (e.g., when
follow from the above arguments (e.g., when 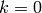 , we have
, we have 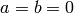 and
basis
and
basis  ). Choose some pair of nonnegative integers
). Choose some pair of nonnegative integers 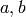 such that
such that 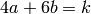 . The form
. The form
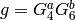 is not a cusp form, since it is nonzero at
is not a cusp form, since it is nonzero at  .
Now suppose
.
Now suppose 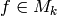 is arbitrary. Since
is arbitrary. Since 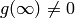 , there
exists
, there
exists 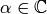 such that
such that 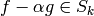 . Then by
Theorem 2.14, there is
. Then by
Theorem 2.14, there is 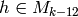 such that
such that 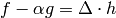 . By induction,
. By induction, 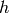 is a polynomial in
is a polynomial in
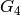 and
and 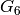 of the required type, and so is
of the required type, and so is  , so
, so  is
as well. Thus
is
as well. Thus
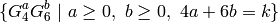
spans 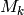 .
.
Suppose there is a nontrivial linear relation between the 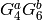 for a given
for a given  . By multiplying the linear relation by a
suitable power of
. By multiplying the linear relation by a
suitable power of 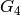 and
and 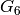 , we may assume that we have
such a nontrivial relation with
, we may assume that we have
such a nontrivial relation with 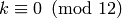 . Now divide the
linear relation by the weight
. Now divide the
linear relation by the weight  form
form 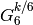 to see that
to see that
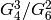 satisfies a polynomial with coefficients in
satisfies a polynomial with coefficients in  (see Exercise 2.4). Hence
(see Exercise 2.4). Hence
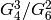 is a root of a polynomial, hence a constant, which is a
contradiction since the
is a root of a polynomial, hence a constant, which is a
contradiction since the  -expansion of
-expansion of 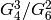 is not
constant.
is not
constant.
Algorithm 2.18
Given integers  and
and  , this algorithm computes
a basis of
, this algorithm computes
a basis of  -expansions for the complex vector
space
-expansions for the complex vector
space 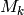 mod
mod 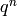 . The
. The  -expansions output
by this algorithm have coefficients in
-expansions output
by this algorithm have coefficients in  .
.
- [Simple Case] If
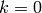 , output the basis with just
, output the basis with just  in it and
terminate; otherwise if
in it and
terminate; otherwise if 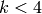 or
or  is odd, output the empty
basis and terminate.
is odd, output the empty
basis and terminate. - [Power Series] Compute
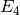 and
and 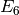 mod
mod 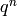 using the
formula from (3) and Section Fast Computation of Bernoulli Numbers.
using the
formula from (3) and Section Fast Computation of Bernoulli Numbers. - [Initialize] Set
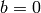 .
. - [Enumerate Basis] For each integer
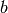 between
between  and
and
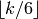 , compute
, compute 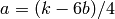 .
If
.
If  is an integer, compute and output the basis
element
is an integer, compute and output the basis
element 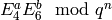 . When computing
. When computing
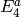 , find
, find
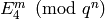 for each
for each 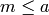 , and save these
intermediate powers, so they can be reused later, and
likewise for powers of
, and save these
intermediate powers, so they can be reused later, and
likewise for powers of 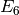 .
.
Proof
This is simply a translation of Theorem 2.17
into an algorithm, since 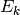 is a nonzero scalar multiple
of
is a nonzero scalar multiple
of 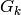 . That the
. That the  -expansions have coefficients
in
-expansions have coefficients
in  follows from (3).
follows from (3).
Example 2.19
We compute a basis for 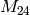 , which is the space with
smallest weight whose dimension is greater than
, which is the space with
smallest weight whose dimension is greater than  .
It has as basis
.
It has as basis 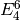 ,
, 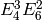 , and
, and 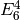 , whose explicit
expansions are
, whose explicit
expansions are
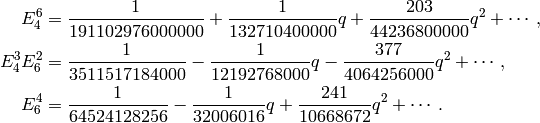
We compute this basis in Sage as follows:
sage: E4 = eisenstein_series_qexp(4, 3)
sage: E6 = eisenstein_series_qexp(6, 3)
sage: E4^6
1/191102976000000 + 1/132710400000*q
+ 203/44236800000*q^2 + O(q^3)
sage: E4^3*E6^2
1/3511517184000 - 1/12192768000*q
- 377/4064256000*q^2 + O(q^3)
sage: E6^4
1/64524128256 - 1/32006016*q + 241/10668672*q^2 + O(q^3)
In Section The Miller Basis, we will discuss the
reduced echelon form basis for 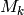 .
.
The Miller Basis¶
Lemma 2.20
The space 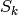 has a basis
has a basis 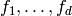 such
that if
such
that if 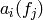 is the
is the 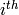 coefficient of
coefficient of 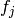 , then
, then
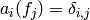 for
for 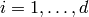 . Moreover
the
. Moreover
the 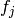 all lie in
all lie in ![\Z[[q]]](_images/math/30d204f5b49a5587d441b79d89f4914df9d5461a.png) . We call this basis the
Miller basis for
. We call this basis the
Miller basis for 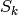 .
.
This is a straightforward construction involving 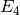 ,
, 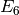 and
and
 . The following proof very closely follows
[Lan95, Ch. X,Thm. 4.4], which in turn follows the
first lemma of V. Miller’s thesis.
. The following proof very closely follows
[Lan95, Ch. X,Thm. 4.4], which in turn follows the
first lemma of V. Miller’s thesis.
Proof
Let 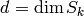 . Since
. Since 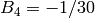 and
and 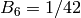 , we note that
, we note that
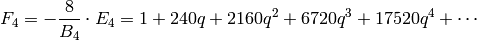
and
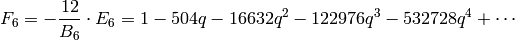
have  -expansions in
-expansions in ![\Z[[q]]](_images/math/30d204f5b49a5587d441b79d89f4914df9d5461a.png) with leading coefficient
with leading coefficient  .
Choose integers
.
Choose integers  such that
such that
with  when
when 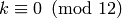 , and let
, and let
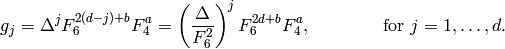
Then it is elementary to check that 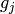 has weight
has weight 
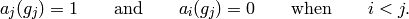
Hence the 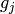 are linearly independent over
are linearly independent over  , so form
a basis for
, so form
a basis for 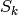 . Since
. Since 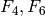 , and
, and  are all in
are all in ![\Z[[q]]](_images/math/30d204f5b49a5587d441b79d89f4914df9d5461a.png) ,
so are the
,
so are the 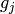 . The
. The 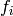 may then be constructed from the
may then be constructed from the 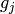 by Gauss elimination. The coefficients of the resulting power series lie in
by Gauss elimination. The coefficients of the resulting power series lie in
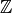 because each time we clear a column we use the power series
because each time we clear a column we use the power series
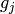 whose leading coefficient is
whose leading coefficient is  (so no denominators are introduced).
(so no denominators are introduced).
Remark 2.21
The basis coming from Miller’s lemma is “canonical”“,
since it is just the reduced row echelon form of any basis.
Also the set of all integral linear combinations of
the elements of the Miller basis are precisely
the modular forms of level  with integral
with integral  -expansion.
-expansion.
We extend the Miller basis to all 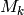 by taking
a multiple of
by taking
a multiple of 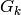 with constant term
with constant term  and subtracting
off the
and subtracting
off the 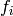 from the Miller basis so that the
coefficients of
from the Miller basis so that the
coefficients of 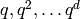 of
the resulting expansion are
of
the resulting expansion are  . We call the extra basis
element
. We call the extra basis
element 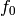 .
.
Example 2.22
If 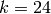 , then
, then 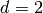 . Choose
. Choose 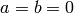 , since
, since 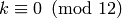 .
Then
.
Then
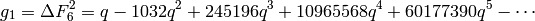
and
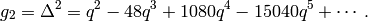
We let 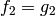 and
and
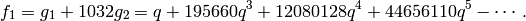
Example 2.23
When 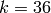 , the Miller basis including
, the Miller basis including 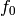 is
is
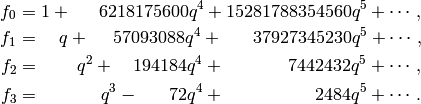
Example 2.24
The Sage command victor_miller_basis computes the Miller
basis to any desired precision given  .
.
sage: victor_miller_basis(28,5)
[
1 + 15590400*q^3 + 36957286800*q^4 + O(q^5),
q + 151740*q^3 + 61032448*q^4 + O(q^5),
q^2 + 192*q^3 - 8280*q^4 + O(q^5)
]
Remark 2.25
To write 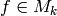 as a polynomial in
as a polynomial in 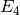 and
and 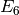 ,
it is wasteful to compute the Miller basis. Instead,
use the upper triangular (but not echelon!) basis
,
it is wasteful to compute the Miller basis. Instead,
use the upper triangular (but not echelon!) basis 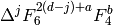 , and match coefficients from
, and match coefficients from 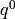 to
to 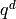 .
.
Hecke Operators¶
In this section we define Hecke operators on level  modular forms and
derive their basic properties. We will not give proofs of the
analogous properties for Hecke operators on higher level modular
forms, since the proofs are clearest in the level
modular forms and
derive their basic properties. We will not give proofs of the
analogous properties for Hecke operators on higher level modular
forms, since the proofs are clearest in the level  case, and the
general case is similar (see, e.g., [Lan95]).
case, and the
general case is similar (see, e.g., [Lan95]).
For any positive integer  , let
, let
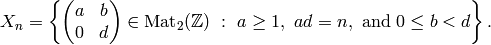
Note that the set 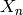 is in bijection with the set of subgroups of
is in bijection with the set of subgroups of
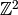 of index
of index  , where
, where 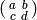 corresponds to
corresponds to
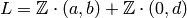 , as one can see using
Hermite normal form, which is the analogue over
, as one can see using
Hermite normal form, which is the analogue over 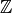 of
echelon form (see Exercise 7.5).
of
echelon form (see Exercise 7.5).
Recall from (?) that
if 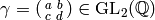 , then
, then
![f^{[\gamma]_k} = \det(\gamma)^{k-1} (cz+d)^{-k} f(\gamma(z)).](_images/math/bff7a83af850b2fdab4cb1b4e8046e96f6f77d5d.png)
Definition 2.26
The 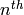 Hecke operator
Hecke operator 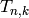 of weight
of weight  is the operator on the set of functions on
is the operator on the set of functions on  defined by
defined by
![T_{n,k}(f) = \sum_{\gamma \in X_n}
f^{[\gamma]_k}.](_images/math/2975551bab9235dcc02d45318fe540c1837257ba.png)
Remark 2.27
It would make more sense to write 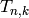 on the right, e.g.,
on the right, e.g.,
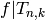 , since
, since 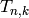 is defined using
a right group action.
However, if
is defined using
a right group action.
However, if 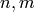 are integers, then the action of
are integers, then the action of 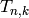 and
and
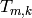 on weakly modular functions commutes (by
Proposition 2.29 below), so it makes no difference
whether we view the Hecke operators of given weight
on weakly modular functions commutes (by
Proposition 2.29 below), so it makes no difference
whether we view the Hecke operators of given weight  as
acting on the right or left.
as
acting on the right or left.
Proposition 2.28
If  is a weakly modular function of weight
is a weakly modular function of weight  , then so is
, then so is
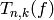 ; if
; if  is a modular function, then so is
is a modular function, then so is 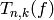 .
.
Proof
Suppose 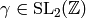 . Since
. Since 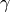 induces an automorphism of
induces an automorphism of 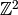 ,
X_n \cdot \gamma = \{ \delta \gamma : \delta\in X_n\}
is also in bijection with the subgroups
of
,
X_n \cdot \gamma = \{ \delta \gamma : \delta\in X_n\}
is also in bijection with the subgroups
of 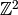 of index
of index  .
For each element
.
For each element 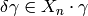 , there
is
, there
is 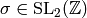 such that
such that 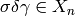 (the
element
(the
element 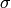 transforms
transforms 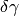 to Hermite normal form),
and the set of elements
to Hermite normal form),
and the set of elements 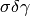 is thus equal to
is thus equal to 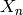 .
Thus
.
Thus
![T_{n,k}(f) = \sum_{\sigma\delta\gamma\in X_n} f^{[\sigma\delta\gamma]_k}
= \sum_{\delta\in X_n} f^{[\delta\gamma]_k}
= T_{n,k}(f)^{[\gamma]_k}.](_images/math/e062631401777247317d291efa1866f952a4f144.png)
A finite sum of meromorphic function is
meromorphic, so 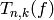 is weakly modular.
If
is weakly modular.
If  is holomorphic on
is holomorphic on  , then
each
, then
each ![f^{[\delta]_k}](_images/math/b4038f97856102c91ed970b75d1e4e69bda3dcac.png) is holomorphic on
is holomorphic on  for
for 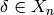 .
A finite sum of holomorphic functions is holomorphic,
so
.
A finite sum of holomorphic functions is holomorphic,
so 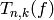 is holomorphic.
is holomorphic.
We will frequently drop  from the notation in
from the notation in 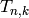 , since
the weight
, since
the weight  is implicit in the modular function to which
we apply the Hecke operator. Henceforth we make the
convention that if we write
is implicit in the modular function to which
we apply the Hecke operator. Henceforth we make the
convention that if we write 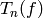 and if
and if  is modular,
then we mean
is modular,
then we mean 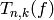 , where
, where  is the weight of
is the weight of  .
.
Proposition 2.29
On weight  modular functions we have
modular functions we have
(4)
and
(5)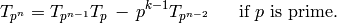
Proof
Let  be a subgroup of index
be a subgroup of index 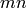 . The quotient
. The quotient 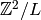 is an
abelian group of order
is an
abelian group of order 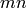 , and
, and 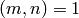 , so
, so 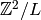 decomposes
uniquely as a direct sum of a subgroup of order
decomposes
uniquely as a direct sum of a subgroup of order  with a subgroup of
order
with a subgroup of
order  . Thus there exists a unique subgroup
. Thus there exists a unique subgroup 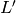 such that
such that
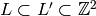 , and
, and 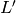 has index
has index  in
in 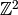 . The
subgroup
. The
subgroup 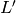 corresponds to an element of
corresponds to an element of 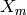 , and the index
, and the index  subgroup
subgroup 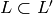 corresponds to multiplying that element on
the right by some uniquely determined element of
corresponds to multiplying that element on
the right by some uniquely determined element of 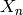 . We thus
have
. We thus
have
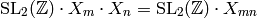
i.e., the set products of elements in 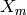 with elements of
with elements of 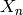 equal the elements of
equal the elements of 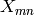 , up to
, up to  -equivalence.
Thus for any
-equivalence.
Thus for any  , we have
, we have
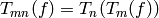 . Applying this formula with
. Applying this formula with  and
and  swapped yields the equality
swapped yields the equality 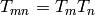 .
.
We will show that 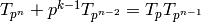 .
Suppose
.
Suppose  is a weight
is a weight  weakly modular function.
Using that
weakly modular function.
Using that
![f^{[\abcd{p}{0}{0}{p}]_k} = (p^2)^{k-1}p^{-k} f = p^{k-2} f](_images/math/a0c72b82e67f74ba14cb69254e42a41e2f04dd00.png) ,
we have
,
we have
![\sum_{x\in X_{p^n}} f^{[x]_k}\,\, +\,\, p^{k-1}\!\!\! \sum_{x\in
X_{p^{n-2}}} f^{[x]_k}
= \sum_{x\in X_{p^n}} f^{[x]_k} \,\,\,+\, p\!\!\!\! \sum_{x\in pX_{p^{n-2}}}
f^{[x]_k}.](_images/math/7c8f9950a3cfd59fa16b60111ce8315954949be6.png)
Also
![T_p T_{p^{n-1}}(f) = \sum_{y\in X_p} \sum_{x\in X_{p^{n-1}}}
(f^{[x]_k})^{[y]_k} = \sum_{x \in X_{p^{n-1}}\cdot X_p}
f^{[x]_k}.](_images/math/c9a5138e7976e44cedb64f4a91556a57ec24b5e0.png)
Thus it suffices to show that 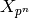 disjoint union
disjoint union  copies
of
copies
of 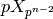 is equal to
is equal to 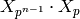 , where we
consider elements with multiplicities and up to left
, where we
consider elements with multiplicities and up to left
 -equivalence (i.e., the left action of
-equivalence (i.e., the left action of  ).
).
Suppose  is a subgroup of
is a subgroup of 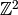 of index
of index 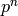 , so
, so  corresponds to an element of
corresponds to an element of 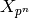 . First suppose
. First suppose  is not
contained in
is not
contained in 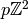 . Then the image of
. Then the image of  in
in 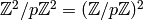 is of order
is of order  , so if
, so if 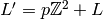 , then
, then
![[\Z^2:L']=p](_images/math/622433093ac24748be582aaa4e6c33180dd595ac.png) and
and ![[L:L']=p^{n-1}](_images/math/88dfabd0870de05840df7d28f33609e3b01d3d3f.png) , and
, and 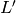 is the only subgroup
with this property. Second, suppose that
is the only subgroup
with this property. Second, suppose that 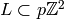 if of
index
if of
index 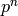 and that
and that 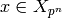 corresponds to
corresponds to  . Then every
one of the
. Then every
one of the 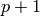 subgroups
subgroups 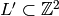 of index
of index  contains
contains  . Thus there are
. Thus there are 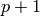 chains
chains 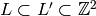 with
with ![[\Z^2:L']=p](_images/math/622433093ac24748be582aaa4e6c33180dd595ac.png) .
.
The chains 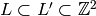 with
with ![[\Z^2:L']=p](_images/math/622433093ac24748be582aaa4e6c33180dd595ac.png) and
and
![[\Z^2:L]=p^{n-1}](_images/math/342dacddc04c5b8e4d3a46dea8035f0b056ea7ef.png) are in bijection with the elements of
are in bijection with the elements of
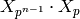 . On the other hand the union of
. On the other hand the union of 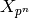 with
with
 copies of
copies of 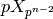 corresponds to the subgroups
corresponds to the subgroups  of index
of index
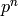 , but with those that contain
, but with those that contain 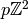 counted
counted 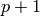 times. The
structure of the set of chains
times. The
structure of the set of chains 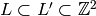 that we
derived in the previous paragraph gives the result.
that we
derived in the previous paragraph gives the result.
Corollary 2.30
The Hecke operator 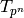 , for prime
, for prime  , is a polynomial
in
, is a polynomial
in  with integer coefficients, i.e.,
with integer coefficients, i.e., ![T_{p^n}\in\Z[T_p]](_images/math/14242ccaa8ee4a0a3d343e971ab3d103b0d148e6.png) .
If
.
If 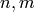 are any integers, then
are any integers, then 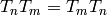
Proof
The first statement follows from (5) of
Proposition 2.29. It then follows that
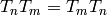 when
when  and
and  are both powers of a single prime
are both powers of a single prime  .
Combining this with (4) gives the second
statement in general.
.
Combining this with (4) gives the second
statement in general.
Proposition 2.31
Let 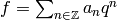 be a modular function
of weight
be a modular function
of weight  .
Then
.
Then
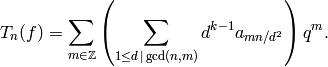
In particular, if 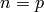 is prime, then
is prime, then
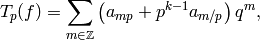
where 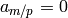 if
if 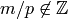 .
.
Proof
This is proved in [Ser73, Section VII.5.3] by writing
out 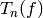 explicitly and using that
explicitly and using that
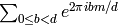 is
is  if
if 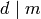 and
and  otherwise.
otherwise.
Corollary 2.32
The Hecke operators preserve 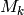 and
and 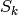 .
.
Remark 2.33
Alternatively, for 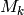 the above corollary is
Proposition 2.28, and for
the above corollary is
Proposition 2.28, and for 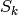 we see from the
definitions that if
we see from the
definitions that if 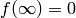 , then
, then 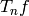 also vanishes
at
also vanishes
at  .
.
Example 2.34
Recall from (3) that
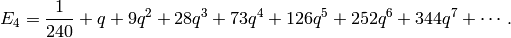
Using the formula of Proposition 2.31, we see that
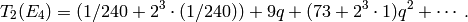
Since 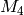 has dimension
has dimension  and since we have proved that
and since we have proved that  preserves
preserves 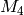 , we know that
, we know that  acts as a scalar. Thus
we know just from the constant coefficient of
acts as a scalar. Thus
we know just from the constant coefficient of 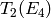 that
that
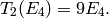
More generally, for  prime we see by inspection of
the constant coefficient of
prime we see by inspection of
the constant coefficient of 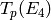 that
that
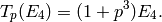
In fact
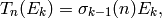
for any integer 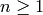 and even weight
and even weight 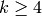 .
.
Example 2.35
By Corollary Corollary 2.32, the Hecke operators  also
preserve the subspace
also
preserve the subspace 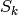 of
of 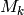 . Since
. Since 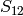 has dimension
has dimension
 (spanned by
(spanned by  ), we see that
), we see that  is an eigenvector
for every
is an eigenvector
for every  . Since the coefficient of
. Since the coefficient of  in the
in the  -expansion
of
-expansion
of  is
is  , the eigenvalue of
, the eigenvalue of  on
on  is the
is the 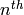 coefficient of
coefficient of  . Since
. Since 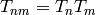 for
for 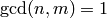 ,
we have proved the nonobvious fact that the
Ramanujan function
,
we have proved the nonobvious fact that the
Ramanujan function 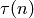 that gives the
that gives the 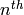 coefficient of
coefficient of  is a multiplicative function, i.e.,
if
is a multiplicative function, i.e.,
if 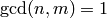 , then
, then 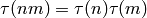 .
.
Remark 2.36
The Hecke operators respect the decomposition
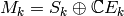 , i.e., for all
, i.e., for all  the series
the series 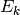 are
eigenvectors for all
are
eigenvectors for all  .
.
Computing Hecke Operators¶
This section is about how to compute matrices
of Hecke operators on 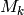 .
.
Algorithm 2.37
This algorithm computes the matrix of the Hecke operator  on the
Miller basis for
on the
Miller basis for 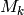 .
.
[Dimension] Compute
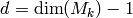 using
Corollary 2.16.
using
Corollary 2.16.[Basis] Using Lemma 2.20, compute the echelon basis
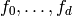 for
for 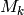
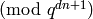 .
.[Hecke operator] Using Proposition 2.31, compute for each
 the image
the image 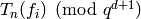 .
.[Write in terms of basis] The elements
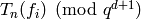 determine linear combinations of
determine linear combinations of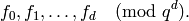
These linear combinations are easy to find once we compute
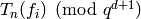 , since our basis of
, since our basis of 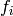 is in
echelon form. The linear combinations are just the coefficients
of the power series
is in
echelon form. The linear combinations are just the coefficients
of the power series 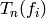 up to and including
up to and including 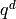 .
.[Write down matrix] The matrix of
 acting from the right
relative to the basis
acting from the right
relative to the basis 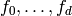 is the matrix whose
rows are the linear combinations found in the previous step,
i.e., whose rows are the coefficients of
is the matrix whose
rows are the linear combinations found in the previous step,
i.e., whose rows are the coefficients of 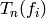 .
.
Proof
By Proposition 2.31, the 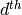 coefficient
of
coefficient
of 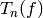 involves only
involves only 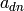 and smaller-indexed coefficients
of
and smaller-indexed coefficients
of  . We need only compute a modular form
. We need only compute a modular form  modulo
modulo 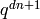 in
order to compute
in
order to compute 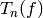 modulo
modulo 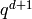 .
Uniqueness in step (4) follows from Lemma 2.20
above.
.
Uniqueness in step (4) follows from Lemma 2.20
above.
Example 2.38
We compute the Hecke operator  on
on 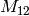 using the above
algorithm.
using the above
algorithm.
[Compute dimension] We have
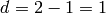 .
.[Compute basis] Compute up to (but not including) the coefficient of
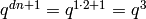 . As given in
the proof of Lemma 2.20, we have
. As given in
the proof of Lemma 2.20, we have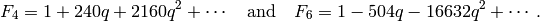
Thus $M_{12}$ has basis
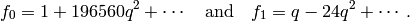
Sage does the arithmetic in the above calculation as follows:
sage: R.<q> = QQ[['q']] sage: F4 = 240 * eisenstein_series_qexp(4,3) sage: F6 = -504 * eisenstein_series_qexp(6,3) sage: F4^3 1 + 720*q + 179280*q^2 + O(q^3) sage: Delta = (F4^3 - F6^2)/1728; Delta q - 24*q^2 + O(q^3) sage: F4^3 - 720*Delta 1 + 196560*q^2 + O(q^3)
[Compute Hecke operator] In each case letting
 denote
the
denote
the  coefficient of
coefficient of 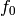 or
or 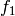 , respectively, we
have
, respectively, we
have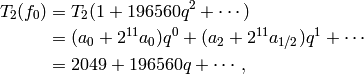
and
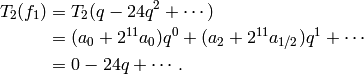
(Note that
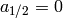 .)
.)[Write in terms of basis] We read off at once that
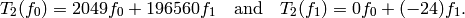
[Write down matrix] Thus the matrix of
 , acting from the
right on the basis
, acting from the
right on the basis 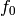 ,
, 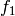 , is
, is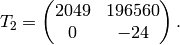
As a check note that the characteristic polynomial of  is
is
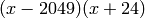 and that
and that 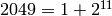 is the sum of the
is the sum of the
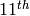 powers of the divisors of
powers of the divisors of  .
.
Example 2.39
The Hecke operator  on
on 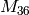 with respect to the echelon
basis is
with respect to the echelon
basis is
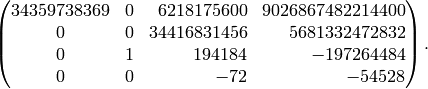
It has characteristic polynomial
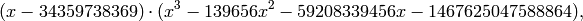
where the cubic factor is irreducible.
The echelon_form command creates the space of modular forms but with basis in echelon form (which is not the default).
sage: M = ModularForms(1,36, prec=6).echelon_form()
sage: M.basis()
[
1 + 6218175600*q^4 + 15281788354560*q^5 + O(q^6),
q + 57093088*q^4 + 37927345230*q^5 + O(q^6),
q^2 + 194184*q^4 + 7442432*q^5 + O(q^6),
q^3 - 72*q^4 + 2484*q^5 + O(q^6)
]
Next we compute the matrix of the Hecke operator  .
.
sage: T2 = M.hecke_matrix(2); T2
[34359738369 0 6218175600 9026867482214400]
[ 0 0 34416831456 5681332472832]
[ 0 1 194184 -197264484]
[ 0 0 -72 -54528]
Finally we compute and factor its characteristic polynomial.
sage: T2.charpoly().factor()
(x - 34359738369) * (x^3 - 139656*x^2 - 59208339456*x - 1467625047588864)
The following is a famous open problem about Hecke operators on
modular forms of level  . It generalizes our above observation that
the characteristic polynomial of
. It generalizes our above observation that
the characteristic polynomial of  on
on 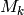 , for
, for 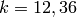 ,
factors as a product of a linear factor and an irreducible factor.
,
factors as a product of a linear factor and an irreducible factor.
Conjuecture 2.40
The characteristic polynomial of  on
on 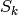 is irreducible for
any
is irreducible for
any  .
.
Kevin Buzzard observed that in several specific cases the Galois group of
the characteristic polynomial of  is the full symmetric group
(see [Buz96]). See also [FJ02] for more
evidence for the following conjecture:
is the full symmetric group
(see [Buz96]). See also [FJ02] for more
evidence for the following conjecture:
Conjuecture 2.41
For all primes  and all even
and all even 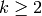 the characteristic
polynomial of
the characteristic
polynomial of 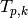 acting on
acting on 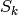 is irreducible.
is irreducible.
Fast Computation of Fourier Coefficients¶
How difficult is it to compute prime-indexed coefficients of
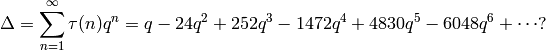
Theorem 2.42
Let  be a prime. There is a probabilistic algorithm to compute
be a prime. There is a probabilistic algorithm to compute
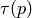 , for prime
, for prime  , that has expected running time polynomial
in
, that has expected running time polynomial
in 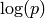
Proof
See [ECdJ+06].
More generally, if 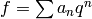 is an eigenform in some space
is an eigenform in some space
 , where
, where 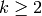 , then one expects that there is an
algorithm to compute
, then one expects that there is an
algorithm to compute 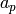 in time polynomial in
in time polynomial in 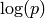 . Bas
Edixhoven, Jean-Marc Couveignes and Robin de Jong have proved that
. Bas
Edixhoven, Jean-Marc Couveignes and Robin de Jong have proved that
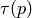 can be computed in polynomial time; their approach involves
sophisticated techniques from arithmetic geometry (e.g., ‘etale
cohomology, motives, Arakelov theory). The ideas they use are inspired
by the ones introduced by Schoof, Elkies and Atkin for quickly
counting points on elliptic curves over finite fields (see
[Sch95]).
can be computed in polynomial time; their approach involves
sophisticated techniques from arithmetic geometry (e.g., ‘etale
cohomology, motives, Arakelov theory). The ideas they use are inspired
by the ones introduced by Schoof, Elkies and Atkin for quickly
counting points on elliptic curves over finite fields (see
[Sch95]).
Edixhoven describes (in an email to the author) the strategy as follows:
- We compute the mod
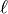 Galois representation
Galois representation 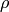 associated
to
associated
to  . In particular, we produce a polynomial
. In particular, we produce a polynomial  such that
such that
![\Q[x]/(f)](_images/math/a27f547d7ccef1a3d0d72faf6ea89c499211f71a.png) is the fixed field of
is the fixed field of 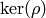 . This is then used
to obtain
. This is then used
to obtain 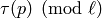 and to do a Schoof-like algorithm
for computing
and to do a Schoof-like algorithm
for computing 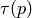 .
. - We compute the field of definition of suitable points of
order
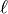 on the modular Jacobian
on the modular Jacobian 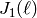 to do part (1) (see
[DS05, Ch. 6] for the definition of
to do part (1) (see
[DS05, Ch. 6] for the definition of 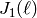 ).
). - The method is to approximate the polynomial
 in some sense
(e.g., over the complex numbers or modulo many small primes
in some sense
(e.g., over the complex numbers or modulo many small primes  )
and to use an estimate from Arakelov theory to determine a
precision that will suffice.
)
and to use an estimate from Arakelov theory to determine a
precision that will suffice.
Fast Computation of Bernoulli Numbers¶
This section, which was written jointly with Kevin McGown, is about
computing the Bernoulli numbers 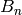 , for
, for 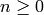 , defined in
Section Fourier Expansions of Eisenstein Series by
, defined in
Section Fourier Expansions of Eisenstein Series by
(6)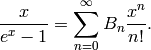
One way to compute 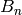 is to multiply both sides of
(?) by
is to multiply both sides of
(?) by 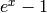 and equate coefficients of
and equate coefficients of
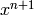 to obtain the recurrence
to obtain the recurrence
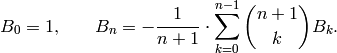
This recurrence provides a straightforward and easy-to-implement
method for calculating 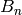 if one is interested in
computing
if one is interested in
computing 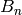 for all
for all  up to some bound.
For example,
up to some bound.
For example,
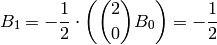
and
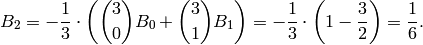
However, computing 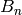 via the recurrence is slow; it requires
summing over many large terms, it requires storing the numbers
via the recurrence is slow; it requires
summing over many large terms, it requires storing the numbers
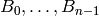 , and it takes only limited advantage of
asymptotically fast arithmetic algorithms. There is also an inductive
procedure to compute Bernoulli numbers that resembles Pascal’s
triangle called the Akiyama-Tanigawa algorithm (see
[Kan00]).
, and it takes only limited advantage of
asymptotically fast arithmetic algorithms. There is also an inductive
procedure to compute Bernoulli numbers that resembles Pascal’s
triangle called the Akiyama-Tanigawa algorithm (see
[Kan00]).
Another approach to computing 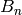 is to use Newton
iteration and asymptotically fast polynomial arithmetic to approximate
is to use Newton
iteration and asymptotically fast polynomial arithmetic to approximate
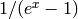 . This method yields a very fast algorithm to compute
. This method yields a very fast algorithm to compute
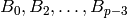 modulo
modulo  .
See [BCS92] for an application of this
method modulo a prime
.
See [BCS92] for an application of this
method modulo a prime  to the verification of
Fermat’s last theorem for irregular primes up to one million.
to the verification of
Fermat’s last theorem for irregular primes up to one million.
Example 2.43
David Harvey implemented the algorithm of [BCS92] in Sage as the command bernoulli_mod_p:
sage: bernoulli_mod_p(23)
[1, 4, 13, 17, 13, 6, 10, 5, 10, 9, 15]
A third way to compute 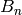 uses
an algorithm based on Proposition 2.8,
which we explain below (Algorithm 2.45).
This algorithm appears to
have been independently invented by several people: by Bernd C.
Kellner (see [Kel06]); by Bill Dayl; and by H. Cohen and
K. Belabas.
uses
an algorithm based on Proposition 2.8,
which we explain below (Algorithm 2.45).
This algorithm appears to
have been independently invented by several people: by Bernd C.
Kellner (see [Kel06]); by Bill Dayl; and by H. Cohen and
K. Belabas.
We compute 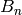 as an exact rational number
by approximating
as an exact rational number
by approximating 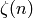 to very high precision using
Proposition 2.8, the
Euler product
to very high precision using
Proposition 2.8, the
Euler product
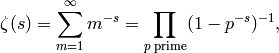
and the following theorem:
Theorem 2.44
For even 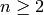 ,
,
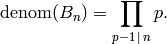
Proof
See [Lan95, Ch. X, Thm. 2.1].
The Number of Digits of 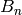 ¶
¶
The following is a new quick way to compute the number of digits of
the numerator of 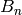 . For example, using it we can compute the
number of digits of
. For example, using it we can compute the
number of digits of 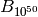 in less than a second.
in less than a second.
By Theorem 2.44 we have
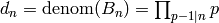 . The number of digits of
the numerator is thus
. The number of digits of
the numerator is thus
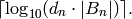
But
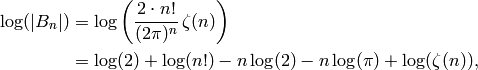
and 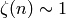 so
so 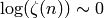 .
Finally, Stirling’s formula (see [Ahl78, pg. 198–206])
gives a fast way to compute
.
Finally, Stirling’s formula (see [Ahl78, pg. 198–206])
gives a fast way to compute 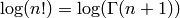 :
:
(7)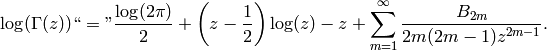
We put quotes around the equality sign because 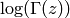 does
not converge to its Laurent series. Indeed, note that for any fixed
value of
does
not converge to its Laurent series. Indeed, note that for any fixed
value of  the summands on the right side go to
the summands on the right side go to  as
as
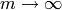 ! Nonetheless, we can use this formula to very efficiently
compute
! Nonetheless, we can use this formula to very efficiently
compute 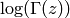 , since if we truncate the sum, then the
error is smaller than the next term in the infinite sum.
, since if we truncate the sum, then the
error is smaller than the next term in the infinite sum.
Computing 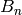 Exactly¶
Exactly¶
We return to the problem of computing 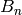 . Let
. Let
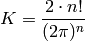
so 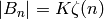 . Write
. Write
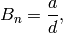
with 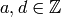 ,
, 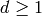 , and
, and 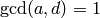 .
It is elementary
to show that
.
It is elementary
to show that 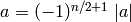 for even
for even 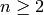 .
Suppose that using the Euler product we approximate
.
Suppose that using the Euler product we approximate
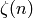 from below by a number
from below by a number  such that
such that
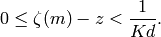
Then 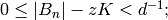 hence
hence 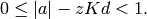 It follows that
It follows that 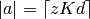 and hence
and hence 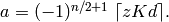
It remains to compute  .
Consider the following problem:
given
.
Consider the following problem:
given 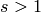 and
and
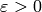 , find
, find 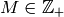 so that
so that
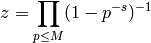
satisfies 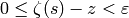 .
We always have
.
We always have 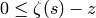 .
Also,
.
Also,
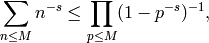
so
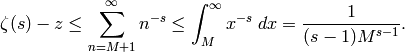
Thus if 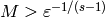 , then
, then
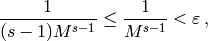
so 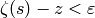 , as required.
For our purposes, we have
, as required.
For our purposes, we have  and
and 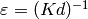 ,
so it suffices to take
,
so it suffices to take 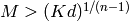 .
.
Algorithm 2.45
Given an integer 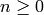 , this algorithm computes
the Bernoulli number
, this algorithm computes
the Bernoulli number 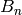 as an exact rational number.
as an exact rational number.
- [Special cases] If
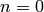 , return
, return  ; if
; if 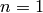 , return
, return 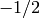 ;
if
;
if 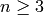 is odd, return
is odd, return  .
. - [Factorial factor] Compute
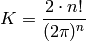 to sufficiently many digits of precision so
the ceiling in step (6) is uniquely determined
(this precision can be determined using
Section The Number of Digits of ).
to sufficiently many digits of precision so
the ceiling in step (6) is uniquely determined
(this precision can be determined using
Section The Number of Digits of ). - [Denominator] Compute
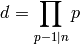 .
. - [Bound] Compute
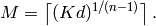
- [Approximate
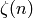 ] Compute
] Compute
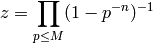 .
. - [Numerator] Compute
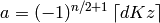 .
. - [Output
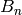 ] Return
] Return 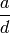 .
.
In step (5) use a sieve to compute all primes
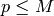 efficiently (which is fast, since
efficiently (which is fast, since  is so small). In
step (4) we may replace
is so small). In
step (4) we may replace  by any integer greater
than the one specified by the formula, so we do not have to compute
by any integer greater
than the one specified by the formula, so we do not have to compute
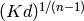 to very high precision.
to very high precision.
In Section Computing Generalized Bernoulli Numbers Analytically below we will generalize the above algorithm.
Example 2.46
We illustrate Algorithm 2.45 by computing 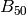 .
Using 135 binary digits of precision, we compute
.
Using 135 binary digits of precision, we compute
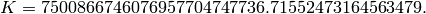
The divisors of  are
are 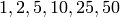 , so
, so
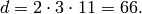
We find 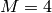 and compute
and compute
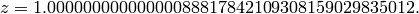
Finally we compute
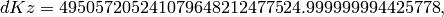
so
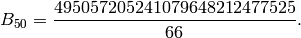
Exercises¶
Exercise 2.1
Using Proposition 2.8 and the table found here, compute
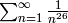 explicitly.
explicitly.
Exercise 2.2
Prove that if 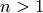 is odd, then the Bernoulli number
is odd, then the Bernoulli number 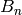 is
is  .
.
Exercise 2.3
Use (3) to write down the coefficients of  ,
,  ,
,
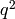 , and
, and 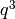 of the Eisenstein series
of the Eisenstein series 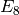 .
.
Exercise 2.4
Suppose  is a positive integer with
is a positive integer with 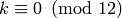 .
Suppose
.
Suppose 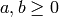 are integers with
are integers with 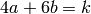 .
.
- Prove
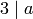 .
. - Show that
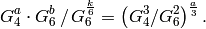
Exercise 2.5
Compute the Miller basis for 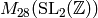 with precision
with precision
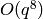 . Your answer will look like Example 2.23.
. Your answer will look like Example 2.23.
Exercise 2.6
Consider the cusp form 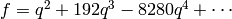 in
in
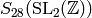 . Write
. Write  as a polynomial in
as a polynomial in 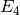 and
and 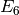 (see Remark 2.25).
(see Remark 2.25).
Exercise 2.7
Let 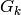 be the weight
be the weight  Eisenstein series from
equation (1). Let
Eisenstein series from
equation (1). Let  be the complex number so that the
constant coefficient of the
be the complex number so that the
constant coefficient of the  -expansion of
-expansion of 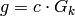 is
is  . Is it always the case that the
. Is it always the case that the  -expansion of
-expansion of  lies
in
lies
in ![\Z[[q]]](_images/math/30d204f5b49a5587d441b79d89f4914df9d5461a.png) ?
?
Exercise 2.8
Compute the matrix of the Hecke operator  on the Miller basis
for
on the Miller basis
for 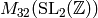 . Then compute its characteristic
polynomial and verify it factors as a product of two irreducible
polynomials.
. Then compute its characteristic
polynomial and verify it factors as a product of two irreducible
polynomials.
What Next? Much of the rest of this book is about methods for
computing subspaces of  for general
for general  and
and  .
These general methods are more complicated than the methods presented
in this chapter, since there are many more modular forms of small
weight and it can be difficult to obtain them. Forms of level
.
These general methods are more complicated than the methods presented
in this chapter, since there are many more modular forms of small
weight and it can be difficult to obtain them. Forms of level  have subtle connections with elliptic curves, abelian varieties, and
motives. Read on for more!
have subtle connections with elliptic curves, abelian varieties, and
motives. Read on for more!