Modular Forms¶
This chapter introduces modular forms and congruence subgroups, which
are central objects in this book. We first introduce the upper half
plane and the group  then recall some definitions from
complex analysis. Next we define modular forms of level
then recall some definitions from
complex analysis. Next we define modular forms of level  followed
by modular forms of general level. In Section Remarks on Congruence Subgroups we
discuss congruence subgroups and explain a
simple way to compute generators for them and determine element
membership. Section Applications of Modular Forms lists applications of
modular forms.
followed
by modular forms of general level. In Section Remarks on Congruence Subgroups we
discuss congruence subgroups and explain a
simple way to compute generators for them and determine element
membership. Section Applications of Modular Forms lists applications of
modular forms.
We assume familiarity with basic number theory, group theory, and complex analysis. For a deeper understanding of modular forms, the reader is urged to consult the standard books in the field, e.g., [Lan95, Ser73, DI95, Miy89, Shi94, Kob84]. See also [DS05], which is an excellent first introduction to the theoretical foundations of modular forms.
Basic Definitions¶
The group
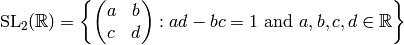
acts on the complex upper half plane
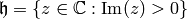
by linear fractional transformations, as follows.
If 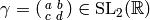 , then for any
, then for any 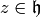 we let
we let
(1)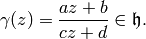
Definition 1.1
The modular group is the group of all matrices
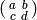 with
with 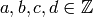 and
and 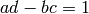 .
.
For example, the matrices
(2)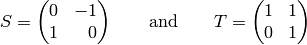
are both elements of  ; the matrix
; the matrix  induces the function
induces the function
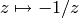 on
on  , and
, and  induces the function
induces the function 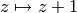 .
.
Theorem 1.2
The group  is generated by
is generated by  and
and  .
.
Proof
See e.g. [Ser73, Section VII.1].
In Sage we compute the group  and its generators as
follows:
and its generators as
follows:
sage: G = SL(2,ZZ); G
Modular Group SL(2,Z)
sage: S, T = G.gens()
sage: S
[ 0 -1]
[ 1 0]
sage: T
[1 1]
[0 1]
Definition 1.3
Let  be an open subset of
be an open subset of  . A function
. A function 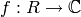 is
holomorphic if
is
holomorphic if  is complex differentiable at every point
is complex differentiable at every point
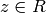 , i.e., for each
, i.e., for each 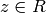 the limit
the limit
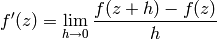
exists, where 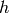 may approach
may approach  along any path. A function
along any path. A function
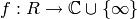 is meromorphic if it is holomorphic
except (possibly) at a discrete set
is meromorphic if it is holomorphic
except (possibly) at a discrete set  of points in
of points in  , and at
each
, and at
each 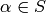 there is a positive integer
there is a positive integer  such that
such that
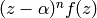 is holomorphic at
is holomorphic at 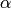 .
.
The function 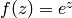 is a holomorphic function on
is a holomorphic function on  ; in
contrast,
; in
contrast, 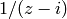 is meromorphic on
is meromorphic on  but not holomorphic
since it has a pole at
but not holomorphic
since it has a pole at  . The function
. The function 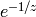 is not
even meromorphic on
is not
even meromorphic on  .
.
Modular forms are holomorphic functions on  that transform in a
particular way under a certain subgroup of
that transform in a
particular way under a certain subgroup of  . Before
defining general modular forms, we define modular forms of level
. Before
defining general modular forms, we define modular forms of level  .
.
Modular Forms of Level  ¶
¶
Definition 1.4
A weakly modular function of weight 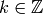 is a
meromorphic function
is a
meromorphic function  on
on  such that for all
such that for all
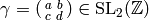 and all
and all 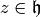 we have
we have
(3)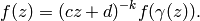
The constant functions are weakly modular of weight  .
There are no nonzero weakly modular functions of odd weight
(see Exercise 1.4), and it is
not obvious that there are any weakly modular functions
of even weight
.
There are no nonzero weakly modular functions of odd weight
(see Exercise 1.4), and it is
not obvious that there are any weakly modular functions
of even weight 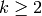 (but there are, as we will see!).
The product of two weakly modular functions of weights
(but there are, as we will see!).
The product of two weakly modular functions of weights 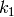 and
and 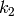 is a weakly modular function of weight
is a weakly modular function of weight 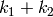 (see Exercise 1.3).
(see Exercise 1.3).
When  is even, (3) has a possibly
more conceptual interpretation; namely
(3) is the same as
is even, (3) has a possibly
more conceptual interpretation; namely
(3) is the same as
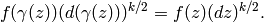
Thus (3) simply says that
the weight  “differential form”
“differential form” 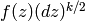 is fixed under the action of every element of
is fixed under the action of every element of
 .
.
By Theorem 1.2, the group  is generated by
the matrices
is generated by
the matrices  and
and  of (2), so to show that a
meromorphic function
of (2), so to show that a
meromorphic function  on
on  is a weakly modular function,
all we have to do is show that for all
is a weakly modular function,
all we have to do is show that for all 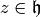 we have
we have
(4)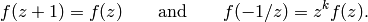
Suppose  is a weakly modular function of weight
is a weakly modular function of weight  . A
Fourier expansion of
. A
Fourier expansion of  , if it exists, is a representation of
, if it exists, is a representation of
 as
as 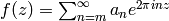 , for all
, for all
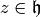 . Let
. Let 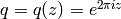 , which we view as a holomorphic
function on
, which we view as a holomorphic
function on  . Let
. Let 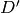 be the open unit disk with the origin
removed, and note that
be the open unit disk with the origin
removed, and note that  defines a map
defines a map 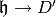 . By
(4) we have
. By
(4) we have 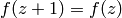 , so there is a function
, so there is a function
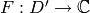 such that
such that 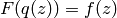 . This function
. This function  is a
complex-valued function on
is a
complex-valued function on 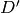 , but it may or may not be well behaved
at
, but it may or may not be well behaved
at  .
.
Suppose that  is well behaved at
is well behaved at  , in the sense that for some
, in the sense that for some
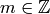 and all
and all  in a neighborhood of
in a neighborhood of  we have the equality
we have the equality
(5)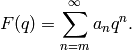
If this is the case, we say that  is
meromorphic at
is
meromorphic at  . If, moreover,
. If, moreover,
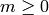 , we say
that
, we say
that  is holomorphic at
is holomorphic at  . We also
call (5) the
. We also
call (5) the  -expansion of
-expansion of  about
about  .
.
Definition 1.5
A modular function of weight  is a weakly modular function
of weight
is a weakly modular function
of weight  that is meromorphic at
that is meromorphic at  .
.
Definition 1.6
A modular form of weight  (and
level
(and
level  ) is a modular function of weight
) is a modular function of weight  that is
holomorphic on
that is
holomorphic on  and at
and at  .
.
If  is a modular form, then there are numbers
is a modular form, then there are numbers
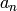 such that for all
such that for all 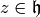 ,
,
(6)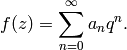
Proposition 1.7
The above series converges for all 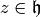 .
.
Proof
The function 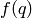 is holomorphic on
is holomorphic on  , so its Taylor series
converges absolutely in
, so its Taylor series
converges absolutely in  .
.
Since 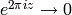 as
as 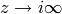 ,
we set
,
we set 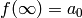 .
.
Definition 1.8
A cusp form of weight  (and level
(and level  ) is a
modular form of weight
) is a
modular form of weight  such that
such that 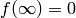 , i.e.,
, i.e., 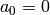 .
.
Let ![\C[[q]]](_images/math/b3805b7f50690462269faabe42010b170a4c021c.png) be the ring of all formal power series in
be the ring of all formal power series in  .
If
.
If 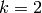 , then
, then 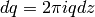 , so
, so 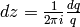 . If
. If 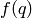 is a cusp form of weight
is a cusp form of weight  , then
, then
![2\pi i f(z) dz
= f(q) \frac{dq}{q} = \frac{f(q)}{q} dq \in \C[[q]] dq.](_images/math/4da7e09ab1cdd7c05885ae85dc67a3e070caa5b0.png)
Thus the differential 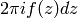 is holomorphic at
is holomorphic at  ,
since
,
since  is a local parameter at
is a local parameter at  .
.
Modular Forms of Any Level¶
In this section we define spaces of modular forms of arbitrary level.
Definition 1.9
A congruence subgroup of
 is any subgroup of
is any subgroup of  that contains
that contains
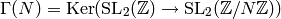
for some positive integer  . The smallest such
. The smallest such  is the
level of
is the
level of  .
.
The most important congruence subgroups in this book are 
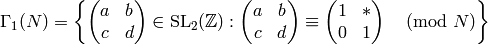
and 
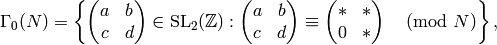
where  means any element. Both groups have level
means any element. Both groups have level  (see
Exercise 1.6).
(see
Exercise 1.6).
Let  be an integer.
Define the weight
be an integer.
Define the weight  right action of
right action of 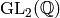 on
the set of all functions
on
the set of all functions 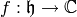 as follows.
If
as follows.
If 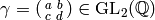 , let
, let
(7)![(f^{[\gamma]_k})(z) = \det(\gamma)^{k-1} (cz+d)^{-k} f(\gamma(z)).](_images/math/41b4caf6dcecc07b4b7fa33577d59ec2b7f3d4c8.png)
Proof
See Exercise 1.7.
Definition 1.11
A weakly modular function of weight  for a
congruence subgroup
for a
congruence subgroup  is a meromorphic
function
is a meromorphic
function 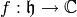 such that
such that
![f^{[\gamma]_k} = f](_images/math/e9f244d60368e99c9a0d210eaac548e3179c93f3.png) for all
for all 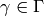 .
.
A central object in the theory of modular forms is the set of cusps
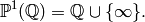
Also, note that if the denominator  or
or 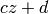 is
is  above,
then
above,
then
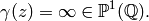
An element 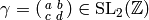 acts on
acts on 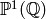 by
by
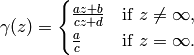
Also, note that if the denominator  or
or 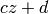 is
is  above,
then
above,
then
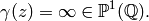
The set of cusps for a congruence subgroup `\Gamma` is the set
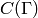 of
of  -orbits of
-orbits of 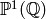 . (We
will often identify elements of
. (We
will often identify elements of 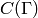 with a representative
element from the orbit.) For example, the lemma below
asserts that if
with a representative
element from the orbit.) For example, the lemma below
asserts that if 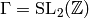 , then there is
exactly one orbit, so
, then there is
exactly one orbit, so ![C(\SL_2(\Z)) = \{[\infty]\}](_images/math/c52d875b5c9f40d503e9ec1a5b5ce648911fad32.png) .
.
Lemma 1.12
For any cusps 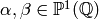 there exists
there exists
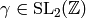 such that
such that 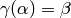 .
.
Proof
This is Exercise 1.8.
Proposition 1.13
For any congruence subgroup  , the set
, the set 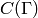 of cusps
is finite.
of cusps
is finite.
Proof
This is Exercise 1.9.
See Section 3.8 of [DS05] and Algorithm 1.33 below for more discussion of cusps and results relevant to their enumeration.
In order to define modular forms for general congruence subgroups, we next explain what it means for a function to be holomorphic on the extended upper half plane
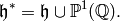
See [Shi94, Section 1.3–1.5], for a detailed
description of the correct topology to consider on 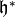 . In
particular, a basis of neighborhoods for
. In
particular, a basis of neighborhoods for 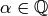 is given by the
sets
is given by the
sets 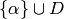 , where
, where  is an open disc in
is an open disc in  that is
tangent to the real line at
that is
tangent to the real line at 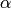 .
.
Recall from Section Modular Forms of Level that a weakly modular
function  on
on  is holomorphic at
is holomorphic at  if its
if its
 -expansion is of the form
-expansion is of the form 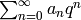 .
.
In order to make sense of holomorphicity of a weakly modular
function  for an arbitrary congruence subgroup
for an arbitrary congruence subgroup  at any
at any
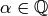 , we first prove a lemma.
, we first prove a lemma.
Lemma 1.14
If 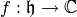 is a weakly modular function of weight
is a weakly modular function of weight  for a congruence subgroup
for a congruence subgroup  and if
and if 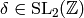 ,
then
,
then ![f^{[\delta]_k}](_images/math/b4038f97856102c91ed970b75d1e4e69bda3dcac.png) is a weakly modular function for
is a weakly modular function for
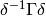 .
.
Proof
If 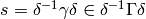 ,
then
,
then
![(f^{[\delta]_k})^{[s]_k} = f^{[\delta s]_k}
= f^{[\delta \delta^{-1}\gamma\delta]_k}
= f^{[\gamma\delta]_k} = f^{[\delta]_k}.](_images/math/b4f054a33d2eab5551d2f9b5c480e8b7025595bf.png)
Fix a weakly modular function  of weight
of weight  for a congruence
subgroup
for a congruence
subgroup  , and suppose
, and suppose 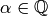 . In
Section Modular Forms of Level we constructed the
. In
Section Modular Forms of Level we constructed the  -expansion of
-expansion of  by
using that
by
using that 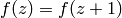 , which held since
, which held since
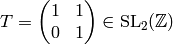 . There are
congruence subgroups
. There are
congruence subgroups  such that
such that 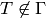 . Moreover,
even if we are interested only in modular forms for
. Moreover,
even if we are interested only in modular forms for  ,
where we have
,
where we have 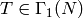 for all
for all  , we will still have to
consider
, we will still have to
consider  -expansions at infinity for modular forms on groups
-expansions at infinity for modular forms on groups
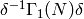 , and these need not contain
, and these need not contain  .
Fortunately,
.
Fortunately, 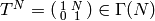 , so a congruence
subgroup of level
, so a congruence
subgroup of level  contains
contains 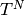 . Thus we have
. Thus we have
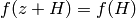 for some positive integer
for some positive integer 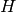 , e.g.,
, e.g., 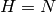 always works, but there may be a smaller choice of
always works, but there may be a smaller choice of 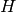 .
The minimal choice of
.
The minimal choice of 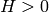 such that
such that
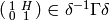 ,
where
,
where 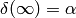 ,
is called the defn{width of the cusp}
,
is called the defn{width of the cusp}
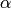 relative to the group
relative to the group  (see Section Computing Widths of Cusps).
When
(see Section Computing Widths of Cusps).
When  is meromorphic at infinity, we obtain
a Fourier expansion
is meromorphic at infinity, we obtain
a Fourier expansion
(8)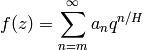
in powers of the function
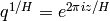 . We say that
. We say that  is holomorphic at
is holomorphic at  if in
(8) we have
if in
(8) we have 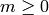 .
.
What about the other cusps 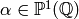 ? By
Lemma 1.12 there is a
? By
Lemma 1.12 there is a 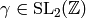 such that
such that
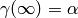 . We declare
. We declare  to be
holomorphic at the cusp
to be
holomorphic at the cusp 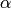 if the weakly modular function
if the weakly modular function ![f^{[\gamma]_k}](_images/math/6598c12197d74870e3b7b4f310ae83d100a42400.png) is
holomorphic at
is
holomorphic at  .
.
Definition 1.15
A modular form of integer weight  for a congruence subgroup
for a congruence subgroup
 is a weakly modular function
is a weakly modular function 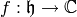 that
is holomorphic on
that
is holomorphic on 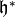 . We let
. We let 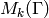 index{
index{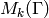 }
denote the space
of weight
}
denote the space
of weight  modular forms of weight
modular forms of weight  for
for  .
.
Proposition 1.16
If a weakly modular function  is holomorphic at a set of
representative elements for
is holomorphic at a set of
representative elements for 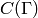 , then it is holomorphic at
every element of
, then it is holomorphic at
every element of 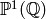 .
.
Proof
Let 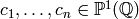 be representatives for the set
of cusps for
be representatives for the set
of cusps for  . If
. If 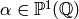 , then there is
, then there is
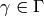 such that
such that 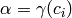 for some
for some  .
By hypothesis
.
By hypothesis  is holomorphic at
is holomorphic at 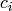 , so if
, so if
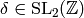 is such that
is such that 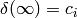 , then
, then
![f^{[\delta]_k}](_images/math/b4038f97856102c91ed970b75d1e4e69bda3dcac.png) is holomorphic at
is holomorphic at  . Since
. Since  is a weakly
modular function for
is a weakly
modular function for  ,
,
(9)![f^{[\delta]_k} = (f^{[\gamma]_k})^{[\delta]_k}
= f^{[\gamma\delta]_k}.](_images/math/f0d168af38b1d44c9c875680f70e65c0438d45c8.png)
But 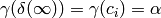 , so
(9) implies that
, so
(9) implies that  is holomorphic
at
is holomorphic
at 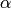 .
.
Remarks on Congruence Subgroups¶
Recall that a congruence subgroup is a subgroup of  ,that contains
,that contains 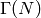 for some
for some  . Any congruence subgroup has
finite index in
. Any congruence subgroup has
finite index in  , since
, since 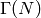 does. What about the
converse: is every finite index subgroup of
does. What about the
converse: is every finite index subgroup of  a congruence subgroup? This is the congruence subgroup problem. One can ask about the congruence subgroup problem with
a congruence subgroup? This is the congruence subgroup problem. One can ask about the congruence subgroup problem with  replaced by many similar groups. If
replaced by many similar groups. If  is a prime, then one can
prove that every finite index subgroup of
is a prime, then one can
prove that every finite index subgroup of ![\SL_2(\Z[1/p])](_images/math/dfd2d3a8bf6dc0dd573a02f4202af4725145c72b.png) is a
congruence subgroup (i.e., contains the kernel of reduction modulo
some integer coprime to
is a
congruence subgroup (i.e., contains the kernel of reduction modulo
some integer coprime to  ), and for any
), and for any 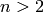 , all finite index
subgroups of
, all finite index
subgroups of 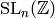 are congruence subgroups (see
[Hum80]). However, there are numerous finite index
subgroups of
are congruence subgroups (see
[Hum80]). However, there are numerous finite index
subgroups of  that are not congruence subgroups. The paper
[Hsu96] contains an algorithm to decide if certain
finite index subgroups are congruence subgroups and gives an example
of a subgroup of index 12 that is not a congruence subgroup.
that are not congruence subgroups. The paper
[Hsu96] contains an algorithm to decide if certain
finite index subgroups are congruence subgroups and gives an example
of a subgroup of index 12 that is not a congruence subgroup.
One can consider modular forms even for noncongruence subgroups. See, e.g., [Tho89] and the papers it references for work on this topic. We will not consider such modular forms further in this book. Note that modular symbols (which we define later in this book) are computable for noncongruence subgroups.
Finding coset representatives for  ,
,  and
and
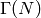 in
in  is straightforward and will be discussed
at length later in this book. To make the problem more explicit, note
that you can quotient out by
is straightforward and will be discussed
at length later in this book. To make the problem more explicit, note
that you can quotient out by 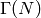 first. Then the question
amounts to finding coset representatives for a subgroup of
first. Then the question
amounts to finding coset representatives for a subgroup of
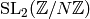 (and lifting), which is reasonably straightforward.
(and lifting), which is reasonably straightforward.
Given coset representatives for a finite index subgroup  of
of
 , we can compute generators for
, we can compute generators for  as follows. Let
as follows. Let  be
a set of coset representatives for
be
a set of coset representatives for  . Let
. Let 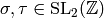 be the matrices denoted by
be the matrices denoted by  and
and  in (2).
Define maps
in (2).
Define maps 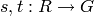 as follows. If
as follows. If 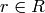 , then there
exists a unique
, then there
exists a unique 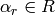 such that
such that 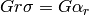 .
Let
.
Let 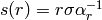 . Likewise, there is a unique
. Likewise, there is a unique
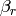 such that
such that 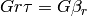 and we let
and we let 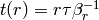 . Note that
. Note that 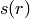 and
and 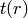 are in
are in  for all
for all  .
Then
.
Then  is generated by
is generated by 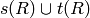 .
.
Proposition 1.17
The above procedure computes generators for  .
.
Proof
Without loss of generality, assume that 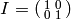 represents the coset of
represents the coset of  . Let
. Let  be an element of
be an element of  .
Since
.
Since 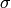 and
and 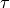 generate
generate  , it is possible to
write
, it is possible to
write  as a product of powers of
as a product of powers of 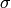 and
and 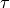 . There is
a procedure, which we explain below with an example in order to
avoid cumbersome notation, which writes
. There is
a procedure, which we explain below with an example in order to
avoid cumbersome notation, which writes  as a product of
elements of
as a product of
elements of 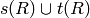 times a right coset
representative
times a right coset
representative 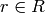 . For example, if
. For example, if
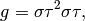
then 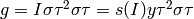 for some
for some 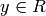 . Continuing,
. Continuing,
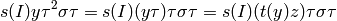
for some 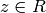 . Again,
. Again,
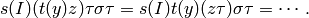
The procedure illustrated above (with an example) makes sense for
arbitrary  and, after carrying it out, writes
and, after carrying it out, writes  as a product
of elements of
as a product
of elements of 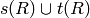 times a right coset
representative
times a right coset
representative 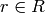 . But
. But 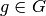 and
and 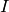 is the right coset
representative for
is the right coset
representative for  , so this right coset representative must
be
, so this right coset representative must
be 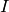 .
.
Remark 1.18
We could also apply the proof of Proposition 1.17 to
write any element of  in terms of the given generators.
Moreover, we could use it to write any element
in terms of the given generators.
Moreover, we could use it to write any element
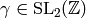 in the form
in the form 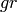 , where
, where 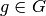 and
and
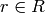 , so we can
decide whether or not
, so we can
decide whether or not 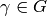 .
.
Computing Widths of Cusps¶
Let  be a congruence subgroup of level
be a congruence subgroup of level  . Suppose
. Suppose
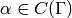 is a cusp, and choose
is a cusp, and choose 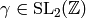 such
that
such
that 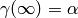 . Recall that the minimal
. Recall that the minimal 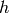 such that
such that
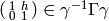 is called the
width of the cusp
is called the
width of the cusp 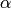 for the group
for the group  . In this
section we discuss how to compute
. In this
section we discuss how to compute 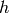 .
.
Algorithm 1.19
Given a congruence subgroup  of level
of level  and a cusp
and a cusp
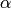 for
for  , this algorithm computes the width
, this algorithm computes the width 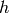 of
of
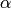 . We assume that
. We assume that  is given by congruence conditions,
e.g.,
is given by congruence conditions,
e.g., 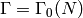 or
or 
[Find
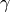 ]: Use the extended Euclidean algorithm
to find
]: Use the extended Euclidean algorithm
to find 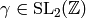 such that
such that 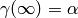 ,
as follows.
,
as follows.If
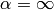 , set
, set 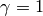 ; otherwise, write
; otherwise, write
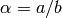 , find
, find 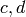 such that
such that 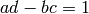 , and set
, and set
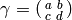 .
.[Compute Conjugate Matrix] Compute the following element of
![\Mat_2(\Z[x])](_images/math/80960d664b1ac896c7b4db501135c93e35e82287.png) :
: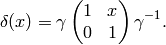
Note that the entries of
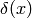 are constant or
linear in
are constant or
linear in  .
.[Solve] The congruence conditions that define
 give rise
to four linear congruence conditions on
give rise
to four linear congruence conditions on  . Use techniques
from elementary number theory (or enumeration) to find the
smallest simultaneous positive solution
. Use techniques
from elementary number theory (or enumeration) to find the
smallest simultaneous positive solution 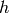 to these four
equations.
to these four
equations.
Example 1.20
Suppose
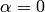 and
and 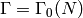 or
or  . Then
. Then
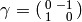 has the property that
has the property that
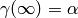 . Next, the congruence condition
is
. Next, the congruence condition
is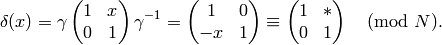
Thus the smallest positive solution is
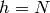 , so the width of
, so the width of  is
is  .
.Suppose
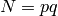 where
where 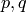 are distinct primes, and let
are distinct primes, and let
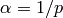 . Then
. Then 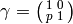 sends
sends  to
to
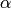 . The congruence condition for
. The congruence condition for 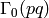 is
is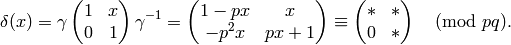
Since
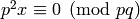 , we see that
, we see that 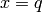 is the smallest
solution. Thus
is the smallest
solution. Thus 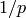 has width
has width  , and symmetrically
, and symmetrically 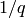 has
width
has
width  .
.
Remark 1.21
For  , once we enforce that the bottom left entry is
, once we enforce that the bottom left entry is
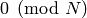 and use that the determinant is 1, the coprimality from
the other two congruences is automatic. So there is one congruence
to solve in the
and use that the determinant is 1, the coprimality from
the other two congruences is automatic. So there is one congruence
to solve in the  case. There are two congruences in
the
case. There are two congruences in
the  case.
case.
Applications of Modular Forms¶
The above definition of modular forms might leave the impression that modular forms occupy an obscure corner of complex analysis. This is not the case! Modular forms are highly geometric, arithmetic, and topological objects that are of extreme interest all over mathematics:
Fermat’s last theorem: Wiles’ proof [Wil95] of Fermat’s last theorem uses modular forms extensively. The work of Wiles et al. on modularity also massively extends computational methods for elliptic curves over
 , because many elliptic curve
algorithms, e.g., for computing
, because many elliptic curve
algorithms, e.g., for computing  -functions, modular degrees,
Heegner points, etc., require that the elliptic curve be modular.
-functions, modular degrees,
Heegner points, etc., require that the elliptic curve be modular.Diophantine equations: Wiles’ proof of Fermat’s last theorem has made available a wide array of new techniques for solving certain diophantine equations. Such work relies crucially on having access to tables or software for computing modular forms. See, e.g., [Dar97], [Mer99], [Che05], [SC03]. (Wiles did not need a computer, because the relevant spaces of modular forms that arise in his proof have dimension
 !) Also, according to Siksek
(personal communication) the paper [BMS06] would “have
been entirely impossible to write without [the algorithms described
in this book].”
!) Also, according to Siksek
(personal communication) the paper [BMS06] would “have
been entirely impossible to write without [the algorithms described
in this book].”Congruent number problem: This ancient open problem is to determine which integers are the area of a right triangle with rational side lengths. There is a potential solution that uses modular forms (of weight
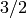 ) extensively (the solution is
conditional on truth of the Birch and Swinnerton-Dyer conjecture,
which is not yet known). See [Kob84].
) extensively (the solution is
conditional on truth of the Birch and Swinnerton-Dyer conjecture,
which is not yet known). See [Kob84].Topology: Topological modular forms are a major area of current research.
Construction of Ramanujan graphs: Modular forms can be used to construct almost optimal expander graphs, which play a role in communications network theory.
Cryptography and Coding Theory: Point counting on elliptic curves over finite fields is crucial to the construction of elliptic curve cryptosystems, and modular forms are relevant to efficient algorithms for point counting (see [Elk98]). Algebraic curves that are associated to modular forms are useful in constructing and studying certain error-correcting codes (see [Ebe02]).
The Birch and Swinnerton-Dyer conjecture: This central open problem in arithmetic geometry relates arithmetic properties of elliptic curves (and abelian varieties) to special values of
 -functions. Most deep results toward this conjecture use
modular forms extensively (e.g., work of Kolyvagin, Gross-Zagier,
and Kato). Also, modular forms are used to compute and prove
results about special values of these
-functions. Most deep results toward this conjecture use
modular forms extensively (e.g., work of Kolyvagin, Gross-Zagier,
and Kato). Also, modular forms are used to compute and prove
results about special values of these  -functions. See
[Wil00].
-functions. See
[Wil00].Serre’s Conjecture on modularity of Galois representation: Let
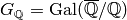 be the Galois group of an algebraic closure
of
be the Galois group of an algebraic closure
of  . Serre conjectured and many people have (nearly!) proved
that every continuous homomorphism
. Serre conjectured and many people have (nearly!) proved
that every continuous homomorphism 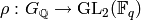 ,
where
,
where 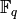 is a finite field and
is a finite field and
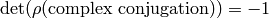 , “arises”
from a modular form. More
precisely, for almost all primes
, “arises”
from a modular form. More
precisely, for almost all primes  the coefficients
the coefficients 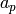 of a
modular (eigen-)form
of a
modular (eigen-)form 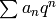 are congruent to the traces of
elements
are congruent to the traces of
elements 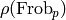 , where
, where 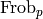 are certain special
elements of
are certain special
elements of 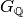 called Frobenius elements. See
[Rib01] and [DS05, Ch. 9].
called Frobenius elements. See
[Rib01] and [DS05, Ch. 9].Generating functions for partitions: The generating functions for various kinds of partitions of an integer can often be related to modular forms. Deep theorems about modular forms then translate into results about partitions. See work of Ramanujan, Gordon, Andrews, and Ahlgren and Ono (e.g., [AO01]).
Lattices: If
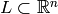 is an even unimodular lattice (the
basis matrix has determinant
is an even unimodular lattice (the
basis matrix has determinant 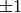 and
and
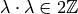 for all
for all 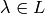 ),
then the theta series
),
then the theta series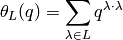
is a modular form of weight
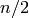 . The coefficient of
. The coefficient of 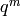 is the number of
lattice vectors with squared length
is the number of
lattice vectors with squared length  . Theorems and
computational methods for modular forms translate into theorems and
computational methods for lattices. For example, the 290 theorem
of M. Bharghava and J. Hanke is a theorem about lattices, which
asserts that an integer-valued quadratic form represents all
positive integers if and only if it represents the integers up to
. Theorems and
computational methods for modular forms translate into theorems and
computational methods for lattices. For example, the 290 theorem
of M. Bharghava and J. Hanke is a theorem about lattices, which
asserts that an integer-valued quadratic form represents all
positive integers if and only if it represents the integers up to
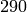 ; it is proved by doing many calculations with modular forms
(both theoretical and with a computer).
; it is proved by doing many calculations with modular forms
(both theoretical and with a computer).
Exercises¶
Exercise 1.1
Suppose 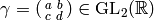 has positive
determinant. Prove that if
has positive
determinant. Prove that if 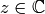 is a complex number with
positive imaginary part, then the imaginary part of
is a complex number with
positive imaginary part, then the imaginary part of
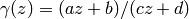 is also positive.
is also positive.
Exercise 1.2
Prove that every rational function (quotient of two polynomials)
is a meromorphic function on  .
.
Exercise 1.3
Suppose  and
and  are weakly modular functions for a congruence
subgroup
are weakly modular functions for a congruence
subgroup  with
with 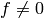 .
.
- Prove that the product
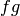 is a weakly modular function for
is a weakly modular function for
 .
. - Prove that
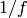 is a weakly modular function for
is a weakly modular function for  .
. - If
 and
and  are modular functions, show that
are modular functions, show that 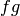 is a modular function for
is a modular function for  .
. - If
 and
and  are modular forms, show that
are modular forms, show that 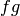 is a modular form for
is a modular form for  .
.
Exercise 1.4
Suppose  is a weakly modular function of odd weight
is a weakly modular function of odd weight  and
level
and
level  for some
for some  .
Show that
.
Show that 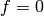 .
.
Exercise 1.5
Prove that 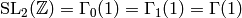 .
.
Exercise 1.6
- Prove that
 is a group.
is a group. - Prove that
 has finite index in
has finite index in  (Hint: It contains the kernel of the homomorphism
(Hint: It contains the kernel of the homomorphism
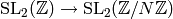 .)
.) - Prove that
 has finite index in
has finite index in  .
. - Prove that
 and
and  have
level
have
level  .
.
Exercise 1.7
Let  be an integer, and for any function
be an integer, and for any function
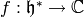 and
and 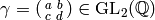 ,
set
,
set
![f^{[\gamma]_k}(z) = \det(\gamma)^{k-1} \cdot (cz+d)^{-k} \cdot f(\gamma(z))](_images/math/2cd717b75e6973506f1b93d56629f513cc586100.png) .
Prove that if
.
Prove that if 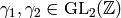 ,
then for all
,
then for all 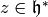 we have
we have
![f^{[\gamma_1 \gamma_2]_k}(z) = ((f^{[\gamma_1]_k})^{[\gamma_2]_k})(z).](_images/math/75d79370144084374d4d4d2136485b8335d5015e.png)
Exercise 1.8
Prove that for any 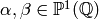 , there exists
, there exists
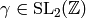 such that
such that 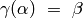 .
.
Exercise 1.9
Prove Proposition 1.13, which asserts that the set
of cusps 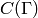 , for any congruence subgroup
, for any congruence subgroup  , is
finite.
, is
finite.
Exercise 1.10
Use Algorithm 1.19 to give an
example of a group  and cusp
and cusp 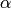 with width
with width  .
.
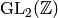 on the set of all functions
on the set of all functions ![f^{[\gamma_1\gamma_2]_k} = (f^{[\gamma_1]_k})^{[\gamma_2]_k}.](_images/math/4b52ccd46cdf461736fc855de3cb4ebadf83c8d7.png)