Next: A Variant of Theorem 5.1.3 Up: Strong Visibility at Higher Previous: Some auxiliary lemmas
By Hypothesis 1 the Tamagawa numbers of ![]() are coprime
to
are coprime
to ![]() . Since
. Since ![]() and
and ![]() are related by an isogeny of degree coprime
to
are related by an isogeny of degree coprime
to ![]() , the Tamagawa numbers of
, the Tamagawa numbers of ![]() are also not divisible by
are also not divisible by ![]() by Lemma 5.2.6. Moreover, note that
by Lemma 5.2.6. Moreover, note that
Let
![]() be the ideal of
be the ideal of
![]() generated by
generated by ![]() and
and
![]() for all integers
for all integers ![]() coprime to
coprime to ![]() .
Note that
.
Note that
![]() is maximal by Lemma 5.2.4.
is maximal by Lemma 5.2.4.
Let ![]() be as in (3), and let
be as in (3), and let
![]() .
Note that if
.
Note that if
![]() then
then
![]() since
since
![]() is attached to a newform, and if, moreover
is attached to a newform, and if, moreover ![]() , then
, then
![]() since the Hecke operators with index coprime to
since the Hecke operators with index coprime to ![]() commute with the degeneracy maps.
Lemma 5.2.1 implies that
commute with the degeneracy maps.
Lemma 5.2.1 implies that
so
where we embed
Suppose for the moment that we have verified that the
hypothesis of Theorem 4.1.1 are satisfied with ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() as above and
as above and
![]() .
Then we obtain an injective homomorphism
.
Then we obtain an injective homomorphism
We then apply Lemma 5.2.2 with ![]() ,
,
![]() ,
, ![]() , and
, and ![]() , respectively, to see that
, respectively, to see that
That
Finally, consider
![]() given by
given by
![]() .
Note that
.
Note that ![]() maps to 0
, since
maps to 0
, since
![]() and the elements of
and the elements of ![]() are of the form
are of the form ![]() .
We have a (not-exact!) sequence of maps
.
We have a (not-exact!) sequence of maps
hence inclusions
It remains to verify the hypotheses of Theorem 4.1.1.
That ![]() is clear from the definition of
is clear from the definition of ![]() . Also,
. Also,
![]() , which is finite.
We explained above when defining
, which is finite.
We explained above when defining ![]() that each of
that each of ![]() and
and ![]() is preserved by
is preserved by ![]() .
Since
.
Since
![]() and
and ![]() is odd the condition
is odd the condition
![]() is satisfied.
That
is satisfied.
That
![]() is finite follows from our hypothesis
that
is finite follows from our hypothesis
that
![]() (by [KL89]).
(by [KL89]).
It remains is to verify that the groups
are 0 for all primes
We will now verify that
![]() .
From the definition of
.
From the definition of ![]() and
and ![]() we have
we have
![]() Let
Let ![]() be as in Lemma 5.2.4 with
be as in Lemma 5.2.4 with
![]() .
The map
.
The map ![]() induces an isogeny of
induces an isogeny of ![]() -power degree
-power degree
Thus there is
By Lemma 5.2.4, we have
![]() , and
by Lemma 5.2.5,
, and
by Lemma 5.2.5,
By [Maz77, § II.14], the quotient
By Hypothesis 2, we have
![]() for each prime
divisor
for each prime
divisor 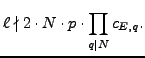 .Since
.Since ![]() is
is ![]() -power isogenous to
-power isogenous to ![]() and
and ![]() is odd, this
verifies the Tamagawa number hypothesis for
is odd, this
verifies the Tamagawa number hypothesis for ![]() . Our hypothesis that
. Our hypothesis that
![]() implies that
implies that
![]() acts on
acts on
![]() as
as
![]() . Thus
. Thus
![]() since
since ![]() is odd.
This completes the proof.
is odd.
This completes the proof.
![]()
William Stein 2006-06-21