Remark 4.1.2
Applying the above result for
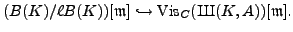
, we recover the result of Agashe and Stein in the case when
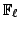
has
Mordell-Weil rank zero. We could relax the hypothesis that
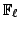
is finite and instead give a bound on
the dimension of the kernel of (
1) in terms of the rank of
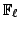
similar to the bound
in [
AS02, Thm. 3.1]. We will not need this stronger result in our paper.