Next: Some auxiliary lemmas Up: Strong Visibility at Higher Previous: Strong Visibility at Higher
Also,
The reason we replace
For a positive integer ![]() , let
, let
We call the number 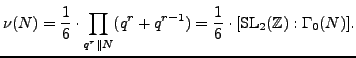 the Sturm bound (see [Stu87]).
the Sturm bound (see [Stu87]).
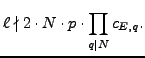 ,
,
for all primes
where
William Stein 2006-06-21