Next: Proof of Theorem 5.1.3 Up: Strong Visibility at Higher Previous: Strongly visible subgroups
Assume that
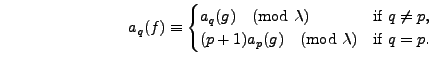 .
Let
.
Let
of subgroups of
where
By [Rib90b, Lem. 1], the operator
![]() on
on ![]() acts as
acts as ![]() on
on
![]() .
Consider the action of
.
Consider the action of ![]() on the 2-dimensional vector space spanned by
on the 2-dimensional vector space spanned by
![]() . The matrix
of
. The matrix
of ![]() with respect to this basis is
with respect to this basis is
In particular, neither of
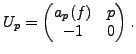 and
and 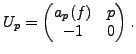 and
and
Thus we can choose an algebraic integer
is an eigenvector of
for all integers
By [Stu87], we have
![]() , so
, so
![]() for all primes
for all primes ![]() . Thus by the
Brauer-Nesbitt theorem [CR62], the 2-dimensional
. Thus by the
Brauer-Nesbitt theorem [CR62], the 2-dimensional
![]() -representations
-representations
![]() and
and
![]() are isomorphic.
are isomorphic.
Let
![]() be a maximal ideal of the Hecke algebra
be a maximal ideal of the Hecke algebra
![]() that annihilates the module
that annihilates the module
![]() .
Note that
.
Note that
![]() since
since
![]() and
and
![]() is irreducible as a
is irreducible as a
![]() -module.
The maximal ideal
-module.
The maximal ideal
![]() gives rise to a Galois representation
gives rise to a Galois representation
![]() isomorphic to
isomorphic to
![]() ,
which is irreducible since the Galois module
,
which is irreducible since the Galois module
![]() is irreducible. Finally, we apply
[Wil95, Thm. 2.1(i)] for
is irreducible. Finally, we apply
[Wil95, Thm. 2.1(i)] for
![]() (i.e.,
(i.e.,
![]() ) to conclude
that
) to conclude
that
![]() , i.e., the representation
, i.e., the representation
![]() occurs with multiplicity
one in
occurs with multiplicity
one in ![]() .
Thus
.
Thus
such that
Thus
Define tex2html_wrap_inline$S$ by the exact sequence displaymath 0 &rarr#to;R &rarr#to;T(N) &rarr#to;S &rarr#to;0. Let tex2html_wrap_inline$&ell#ell;$ be any prime. Then we have an exact sequence displaymath R&otimes#otimes;F_&ell#ell;&rarr#to;T(N)&otimes#otimes;F_&ell#ell;&rarr#to;S&otimes#otimes;F_&ell#ell;&rarr#to;0. Using what we did above,for each prime tex2html_wrap_inline$p&mid#mid;M$ we find a prime tex2html_wrap_inline$q&nmid#nmid;M$ such that tex2html_wrap_inline$T_q &equiv#equiv;T_p$ on tex2html_wrap_inline$J[&ell#ell;]$. Thus tex2html_wrap_inline$R&otimes#otimes;F_&ell#ell;&rarr#to;T&otimes#otimes;F_&ell#ell;$is surjective, hence tex2html_wrap_inline$S &otimes#otimes;F_&ell#ell;=0$. Since tex2html_wrap_inline$T$ is a finitely generated abelian group, so is tex2html_wrap_inline$S$, so we must have tex2html_wrap_inline$S=0$.
where the isomorphism is an isomorphism of
Clearly this homomorphism is injective. It is also surjective as every element
William Stein 2006-06-21