Next: Euler's Criterion Up: Quadratic Reciprocity Previous: Quadratic Reciprocity Contents Index
so
The quadratic reciprocity theorem is the deepest theorem that we
will prove in this book. It connects the question of whether or
not ![]() is a quadratic residue modulo
is a quadratic residue modulo ![]() to the question of
whether
to the question of
whether ![]() is a quadratic residue modulo each of the prime divisors
of
is a quadratic residue modulo each of the prime divisors
of ![]() . To express it precisely, we introduce some new notation.
. To express it precisely, we introduce some new notation.

We call this symbol the Legendre Symbol.
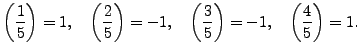
This notation is well entrenched in the literature even though it
is also the notation for ``![]() divided by
divided by ![]() ''; be careful
not to confuse the two.
''; be careful
not to confuse the two.
sage: legendre_symbol(2,3) -1 sage: legendre_symbol(1,3) 1 sage: legendre_symbol(3,5) -1 sage: legendre_symbol(Mod(3,5), 5) -1
Since
![]() only depends on
only depends on ![]() , it makes sense
to define
, it makes sense
to define
![]() for
for
![]() to be
to be
![]() for
any lift
for
any lift ![]() of
of ![]() to
to
![]() .
.
Recall (see Definition 3.3.6) that a group
homomorphism
![]() is a map such that for every
is a map such that for every
![]() we have
we have
![]() .
Moreover, we say that
.
Moreover, we say that ![]() is surjective if for every
is surjective if for every
![]() there is an
there is an ![]() with
with
![]() .
The next lemma explains how the quadratic
residue symbol defines a surjective group homomorphism.
.
The next lemma explains how the quadratic
residue symbol defines a surjective group homomorphism.
Since
Note that the powers of
![]()
The symbol
![]() only depends on the residue class of
only depends on the residue class of ![]() modulo
modulo ![]() , so making a table of values
, so making a table of values
![]() for many values
of
for many values
of ![]() would be easy. Would it be easy to make a table of
would be easy. Would it be easy to make a table of
![]() for many
for many ![]() ? Perhaps, since there appears to be a simple pattern in
Table 4.1.
? Perhaps, since there appears to be a simple pattern in
Table 4.1.
Based on similar observations, in the 18th century various mathematicians found a conjectural explanation for the mystery suggested by Table 4.1. Finally, on April 8, 1796, at the age of 19, Gauss proved the following theorem.
We will give two proofs of Gauss's formula relating
![]() to
to
![]() . The first elementary proof is in
Section 4.3, and the second more algebraic proof is in
Section 4.4.
. The first elementary proof is in
Section 4.3, and the second more algebraic proof is in
Section 4.4.
In our example Gauss's theorem implies that
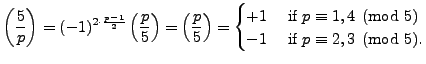
As an application, the following example illustrates how to answer
questions like ``is ![]() a square modulo
a square modulo ![]() '' using
Theorem 4.1.7.
'' using
Theorem 4.1.7.
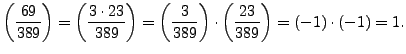
Here
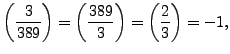
and
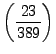 |
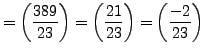 |
|
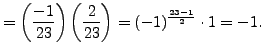 |
sage: legendre_symbol(69,389) 1
Though we know that ![]() is a square modulo
is a square modulo ![]() , we don't know an
explicit
, we don't know an
explicit ![]() such that
such that
![]() ! This is reminiscent
of how we could prove using Theorem 2.1.19 that
certain numbers are composite without knowing a factorization.
! This is reminiscent
of how we could prove using Theorem 2.1.19 that
certain numbers are composite without knowing a factorization.
William 2007-06-01