Existence of Primitive Roots
Recall from Section 2.1.2 that the order of an
element 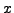 in a finite group is the smallest
in a finite group is the smallest 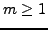 such that
such that
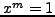 . In this section, we prove that
. In this section, we prove that
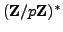 is cyclic by
using the results of Section 2.5.1 to produce an element
of
is cyclic by
using the results of Section 2.5.1 to produce an element
of
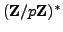 of order
of order 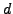 for each prime power divisor
for each prime power divisor 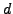 of
of
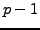 , and then we multiply these together to obtain an element of
order
, and then we multiply these together to obtain an element of
order 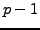 .
.
We will use the following lemma to assemble elements of
each order dividing 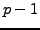 to produce an
element of order
to produce an
element of order 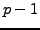 .
.
Lemma 2.5
Suppose
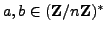 have orders
have orders 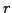 and
and 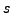 , respectively,
and that
, respectively,
and that
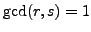 . Then
. Then 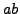 has order
has order 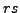 .
.
Proof.
This is a general fact about commuting elements of any group; our proof
only uses that
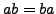
and nothing special about
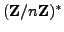
. Since
the order of
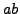
is a divisor of
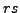
.
Write this divisor as
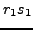
where
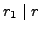
and
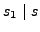
.
Raise both sides of the equation
to the power
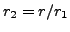
to obtain
Since
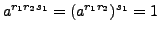
, we have
so
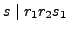
.
Since
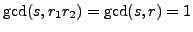
, it follows that
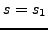
.
Similarly
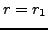
, so the order of
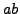
is
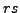
.

Theorem 2.5 (Primitive Roots)
There is a primitive root modulo any prime 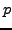 . In particular,
the group
. In particular,
the group
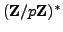 is cyclic.
is cyclic.
Proof.
The theorem is true if
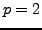
, since
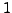
is a primitive root, so we may assume
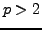
.
Write
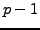
as a product of distinct prime powers
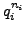
:
By Proposition
2.5.5,
the polynomial
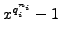
has exactly
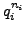
roots, and the polynomial
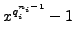
has exactly
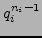
roots.
There are
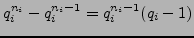
elements
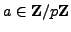
such
that
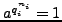
but
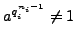
;
each of these elements has order
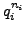
.
Thus for each
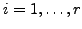
, we can choose an
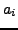
of order
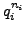
.
Then, using Lemma
2.5.7 repeatedly, we see that
has order
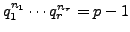
,
so
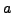
is a primitive root modulo
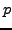
.

Example 2.5
We illustrate the proof of Theorem
2.5.8 when
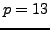
. We have
The polynomial
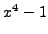
has roots
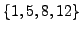
and
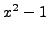
has roots
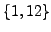
, so we may take
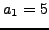
.
The polynomial
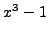
has roots
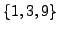
, and we set
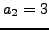
.
Then
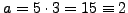
is a primitive root.
To verify this, note that
the successive powers of

are
Example 2.5
Theorem
2.5.8 is false if, e.g.,
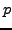
is replaced by a
power of
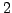
bigger than
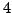
. For example, the four elements of
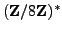
each have order dividing
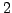
, but
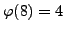
.
Theorem 2.5 (Primitive Roots mod
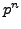
)
Let 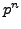 be a power of an odd prime. Then there
is a primitive root modulo
be a power of an odd prime. Then there
is a primitive root modulo 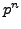 .
.
The proof is left as Exercise 2.28.
Proof.
The primitive roots modulo
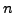
are the generators of
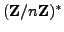
, which by assumption is cyclic of order
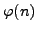
.
Thus they are in bijection with the generators of any cyclic group
of order
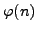
. In particular, the number of primitive roots
modulo
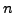
is the same as the number of elements of
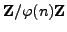
with additive order
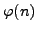
. An element of
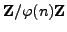
has additive
order
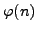
if and only if it is coprime to
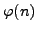
. There
are
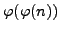
such elements, as claimed.

Example 2.5
For example, there are
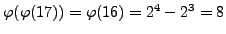
primitive roots mod
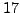
, namely
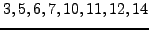
. The
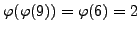
primitive roots modulo
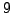
are
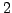
and
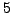
. There are no primitive roots modulo
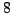
, even though
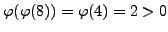
.
William
2007-06-01
![]() to produce an
element of order
to produce an
element of order ![]() .
.