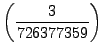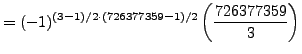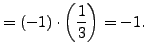Euler's Criterion
Let  be an odd prime and
be an odd prime and 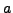 an integer not divisible by
an integer not divisible by  .
Euler
used the existence of primitive roots to show that
.
Euler
used the existence of primitive roots to show that
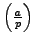 is congruent to
is congruent to
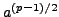 modulo
modulo  . We will use this fact
repeatedly below in both proofs of Theorem 4.1.7.
. We will use this fact
repeatedly below in both proofs of Theorem 4.1.7.
Proof.
The map
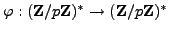
given by
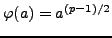
is a group homomorphism, since powering is a group
homomorphism of any abelian group (see Exercise
4.
2).
Let
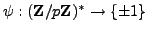
be the homomorphism
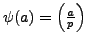
of
Lemma
4.1.4. If

, then
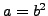
for some
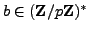
, so
Thus
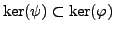
. By Lemma
4.1.4,
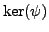
has index
in
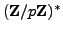
,
i.e.,
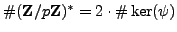
.
Since the kernel of a homomorphism is a group, and the
order of a subgroup divides the order of the group,
we have either
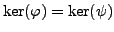
or
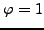
. If
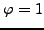
,
the polynomial
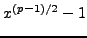
has
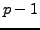
roots in the field
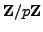
,
which contradicts Proposition
2.5.3. Thus
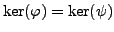
, which proves the proposition.

SAGE Example 4.2
From a computational point of view, Corollary
4.2.3
provides a convenient way to compute
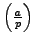
, which we
illustrate in SAGE:
sage: def kr(a, p):
... if Mod(a,p)^((p-1)//2) == 1:
... return 1
... else:
... return -1
sage: for a in range(1,5):
... print a, kr(a,5)
1 1
2 -1
3 -1
4 1
Corollary 4.2
The equation
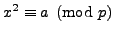 has no solution if and
only if
has no solution if and
only if
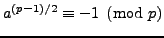 .
Thus
.
Thus
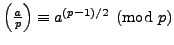 .
.
Proof.
This follows from Proposition
4.2.1 and the
fact that the polynomial
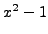
has no roots
besides
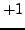
and
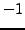
(which follows from
Proposition
2.5.5).

As additional computational motivation for the value of
Corollary 4.2.3, note that to evaluate
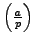 using
Theorem 4.1.7 would not be practical if
using
Theorem 4.1.7 would not be practical if 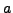 and
and  are
both very large, because it would require factoring
are
both very large, because it would require factoring 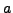 . However,
Corollary 4.2.3 provides a method for evaluating
. However,
Corollary 4.2.3 provides a method for evaluating
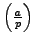 without factoring
without factoring 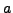 .
.
Example 4.2
Suppose
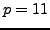
. By squaring each element of
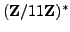
, we see
that the squares modulo
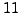
are
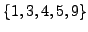
.
We compute
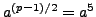
for each
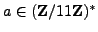
and get
Thus the
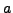
with
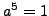
are
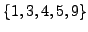
,
just as Proposition
4.2.1 predicts.
Example 4.2
We determine whether or not
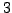
is a square modulo the prime
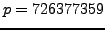
.
Using SAGE we find that
sage: p = 726377359
sage: Mod(3, p)^((p-1)//2)
726377358
so
Thus
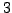
is not a square modulo

. This computation wasn't difficult, but
it would have been tedious by hand. Since
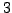
is small,
the law of quadratic reciprocity
provides a way to answer this question, which could easily be carried
out by hand:
William
2007-06-01
![]() using
Theorem 4.1.7 would not be practical if
using
Theorem 4.1.7 would not be practical if ![]() and
and ![]() are
both very large, because it would require factoring
are
both very large, because it would require factoring ![]() . However,
Corollary 4.2.3 provides a method for evaluating
. However,
Corollary 4.2.3 provides a method for evaluating
![]() without factoring
without factoring ![]() .
.