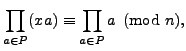Fermat's Little Theorem
Let
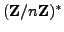 denote the subset of elements
denote the subset of elements
![$ [x] \in \mathbb{Z}/n\mathbb{Z}{}$](img478.png) such that
such that
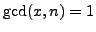 .
.
The set
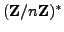 is a group, called the
group of units of the ring
is a group, called the
group of units of the ring
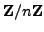 ; it will
be of great interest to us.
Each element of
this group has an order, and Lagrange's theorem from group theory
implies that each element of
; it will
be of great interest to us.
Each element of
this group has an order, and Lagrange's theorem from group theory
implies that each element of
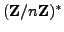 has order that divides
the order of
has order that divides
the order of
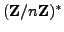 . In elementary number theory this
fact goes by the monicker ``Fermat's Little Theorem'', and we
reprove it from basic principles in this section.
. In elementary number theory this
fact goes by the monicker ``Fermat's Little Theorem'', and we
reprove it from basic principles in this section.
Definition 2.1 (Order of an Element)
Let
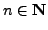
and
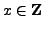
and suppose that
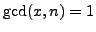
.
The
order of
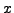
modulo
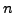
is the smallest
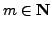
such that
To show that the definition makes sense, we verify
that such an 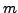 exists. Consider
exists. Consider
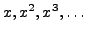 modulo
modulo 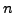 .
There are only finitely many residue classes modulo
.
There are only finitely many residue classes modulo 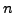 , so we must
eventually find two integers
, so we must
eventually find two integers 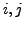 with
with 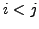 such that
such that
Since
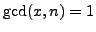 , Proposition 2.1.9 implies that
we can cancel
, Proposition 2.1.9 implies that
we can cancel 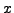 's and conclude that
's and conclude that
SAGE Example 2.1
Use x.multiplicative_order() to compute the
order of an element of
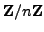
in SAGE.
sage: R = Integers(10)
sage: a = R(3) # create an element of Z/10Z
sage: a.multiplicative_order()
4
Notice that the powers of
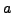
are periodic with period
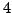
, i.e.,
there are four powers and they repeat:
sage: [a^i for i in range(15)]
[1, 3, 9, 7, 1, 3, 9, 7, 1, 3, 9, 7, 1, 3, 9]
The command range(n) we use
above returns the list of integers between
0
and
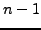
,
inclusive.
For example,
Also, if 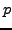 is any prime number then
is any prime number then
In Section 2.2.1, we will prove that 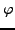 is a
multiplicative function. This will yield an easy way to compute
is a
multiplicative function. This will yield an easy way to compute
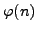 in terms of the prime factorization of
in terms of the prime factorization of 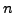 .
.
SAGE Example 2.1
Use the command euler_phi(n) to compute
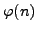
in SAGE:
sage: euler_phi(2007)
1332
Proof.
As mentioned above, Fermat's Little Theorem has the following group-theoretic
interpretation. The set of units in
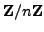
is a group
which has order
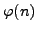
. The theorem then asserts
that the order of an element of
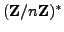
divides the order
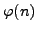
of
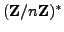
. This is a special case of the more
general fact (Lagrange's theorem) that if
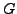
is a finite group and
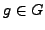
, then the order of
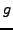
divides the cardinality of
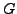
.
We now give an elementary proof of the theorem. Let
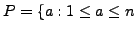
and
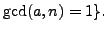
In the same way that we proved Lemma
2.1.11,
we see that the reductions modulo
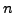
of the elements of
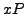
are the same as the reductions of the elements of
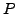
.
Thus
since the products are over the same numbers modulo
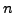
.
Now cancel the
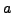
's on both sides to get
as claimed.

SAGE Example 2.1
We illustrate Fermat's Little Theorem using SAGE.
The command Mod(x,n) returns the equivalence
class of
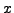
in
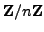
.
sage: n = 20
sage: k = euler_phi(n); k
8
sage: [Mod(x,n)^k for x in range(n) if gcd(x,n) == 1]
[1, 1, 1, 1, 1, 1, 1, 1]
William
2007-06-01
![]() is a group, called the
group of units of the ring
is a group, called the
group of units of the ring
![]() ; it will
be of great interest to us.
Each element of
this group has an order, and Lagrange's theorem from group theory
implies that each element of
; it will
be of great interest to us.
Each element of
this group has an order, and Lagrange's theorem from group theory
implies that each element of
![]() has order that divides
the order of
has order that divides
the order of
![]() . In elementary number theory this
fact goes by the monicker ``Fermat's Little Theorem'', and we
reprove it from basic principles in this section.
. In elementary number theory this
fact goes by the monicker ``Fermat's Little Theorem'', and we
reprove it from basic principles in this section.