


Next: Mazur's letter
Up: No Title
Previous: No Title
Consider a continuous odd Galois representation
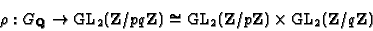 |
(1) |
that is irreducible when reduced modulo p and modulo q.
We say that 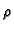 is modular if there exists a
newform f such that
is modular if there exists a
newform f such that
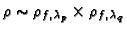 ,
with
,
with 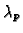 and
and 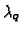 primes lying over p and q,
respectively. Is every mod pq representation modular?
When
primes lying over p and q,
respectively. Is every mod pq representation modular?
When 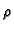 is modular, what is the minimal level
is modular, what is the minimal level
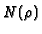 and weight
and weight 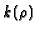 of a newform f giving rise to
of a newform f giving rise to 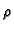 ?
In this section we report on a first investigation, conducted
jointly with B. Mazur, into this question.
?
In this section we report on a first investigation, conducted
jointly with B. Mazur, into this question.
William A. Stein
1999-08-31