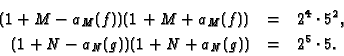Next: N=11, M=23:
Up: Two more examples
Previous: Two more examples
A basis for
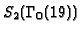 is
is
We find that
The only pair of primes for which 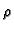 is irreducible is
p=2, q=5. The four classes of newforms at
level
is irreducible is
p=2, q=5. The four classes of newforms at
level
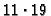 are
are
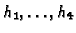 .
The relevant congruences are
.
The relevant congruences are
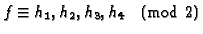 and
and
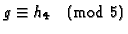 .
Therefore
.
Therefore
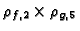 arises from the eigenform h4;
the coefficient a2 of h4satisfies the irreducible polynomial
x7 + x6 - 14x5 - 10x4 + 59x3 + 27x2 - 66x - 30.
Again, we have maximal success.
arises from the eigenform h4;
the coefficient a2 of h4satisfies the irreducible polynomial
x7 + x6 - 14x5 - 10x4 + 59x3 + 27x2 - 66x - 30.
Again, we have maximal success.
William A. Stein
1999-08-31