


Next: Bibliography
Up: Exploration of a mod pq
Previous: Is every modular?
In Table 1.6 we tabulate computations
that address Mazur's letter (see Section 1.1).
We analyzed each pair f, g of newforms of levels N, M,
with
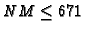 .
Each pair of rows in the table corresponds
to a pair of forms f, g. Let
.
Each pair of rows in the table corresponds
to a pair of forms f, g. Let
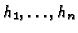 be representatives
for the Galois conjugacy classes of newforms at level NM.
The ``Congruences'' column is a block of columns
that contain, in order,
the primes p,q such that
be representatives
for the Galois conjugacy classes of newforms at level NM.
The ``Congruences'' column is a block of columns
that contain, in order,
the primes p,q such that
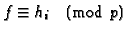 and
and
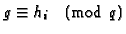 .
The ``Irreducible nonsuccess'' column lists the
pairs p,q, with p and q both non-Eisenstein primes listed
in column two, such that
.
The ``Irreducible nonsuccess'' column lists the
pairs p,q, with p and q both non-Eisenstein primes listed
in column two, such that
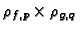 does not arise from
a modular form of level NM. The third column
is empty exactly when we have maximal success; this
occurs for only 4 of the 23 pairs f,g.
The table gives only a small part of the full computation, which
covers all pairs f,g such that NM<2000.
[[A summary of computation up to level 2000 will go here.]]
does not arise from
a modular form of level NM. The third column
is empty exactly when we have maximal success; this
occurs for only 4 of the 23 pairs f,g.
The table gives only a small part of the full computation, which
covers all pairs f,g such that NM<2000.
[[A summary of computation up to level 2000 will go here.]]
Table:
Serre mod pq data for
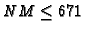
 |
William A. Stein
1999-08-31
