


Next: Serre mod pq table
Up: Exploration of a mod pq
Previous: N=11, M=23:
Is every 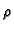 modular?
modular?
As in Mazur's letter (Section 1.1),
consider f,g,p,q with f, g of level N, M, respectively.
Suppose that there is no form h at level NM such that
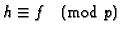 and
and
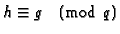 (congruence as in Section 1.2).
Our choice of p and q implies that there is h1 and h2
at level NM such that
(congruence as in Section 1.2).
Our choice of p and q implies that there is h1 and h2
at level NM such that
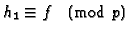 and
and
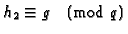 .
Using the Cebotarev Density Theorem (see e.g., [Lan94, VIII.4])
and Ribet's level raising theorem [Rib90]
we see that there are infinitely many primes
.
Using the Cebotarev Density Theorem (see e.g., [Lan94, VIII.4])
and Ribet's level raising theorem [Rib90]
we see that there are infinitely many primes 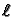 for which
there exists newforms b1 and b2 at level
for which
there exists newforms b1 and b2 at level 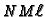 such
that
such
that
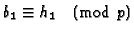 and
and
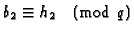 .
Does b1=b2 in one of these infinitely
many cases? More generally, begin with two newforms fand g both of some level N and consider the infinitely
many primes
.
Does b1=b2 in one of these infinitely
many cases? More generally, begin with two newforms fand g both of some level N and consider the infinitely
many primes 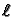 such that there exists h1 and h2of level
such that there exists h1 and h2of level 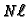 with
with
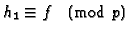 and
and
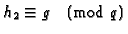 .
Must there always be an
.
Must there always be an 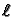 so that we can take h1=h2? If yes, then every mod pqrepresentation is modular; at least, if we admit the classical
Serre conjectures.
so that we can take h1=h2? If yes, then every mod pqrepresentation is modular; at least, if we admit the classical
Serre conjectures.
Answers to the above questions may be viewed as
a generalization of Ribet's level raising
machinery [Rib90].
The introduction of two primes at once obscures
the algebraic interpretation in terms of ideals of the
Hecke algebra; making it appear necessary to find new
arguments.
For this reason, the author suspects that there are non-modular
mod pq representations.
Even if not all mod pq representations are modular,
the question remains of finding the minimal weight and level of
those which are.



Next: Serre mod pq table
Up: Exploration of a mod pq
Previous: N=11, M=23:
William A. Stein
1999-08-31