


Next: Two more examples
Up: Exploration of a mod pq
Previous: Congruence terminology
The first example: N=11, M=17
Consider the first example, in which N=11 and M=17.
The spaces
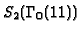 and
and
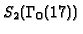 are spanned by newforms f and g, respectively, where
are spanned by newforms f and g, respectively, where
We have
To avoid reducibility we require that
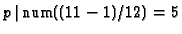 and
and
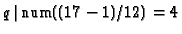 ,
so
only the pair p=2, q=3 remains. The representation
,
so
only the pair p=2, q=3 remains. The representation
is irreducible mod 2 and mod 3.
Choose newforms
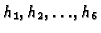 from each Galois conjugacy class
in
from each Galois conjugacy class
in
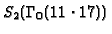 ,
ordered as in Section
,
ordered as in Section ![[*]](cross_ref_motif.gif) .
We find that
.
We find that
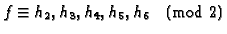 and
and
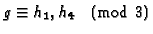 .
Because h4 occurs in both of these lists,
.
Because h4 occurs in both of these lists,
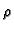 is modular;
is modular; 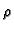 arises from
arises from
where
a2 + 2a - 2=0. We have maximal success.
William A. Stein
1999-08-31
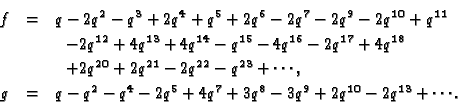
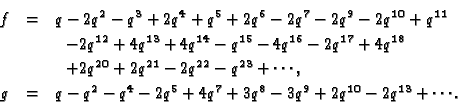
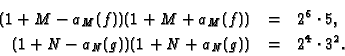
![[*]](cross_ref_motif.gif) .
We find that
.
We find that