


Next: The first example: N=11,
Up: Exploration of a mod pq
Previous: Mazur's letter
Congruence terminology
In order to work entirely over the integers and determine
congruences exactly, we use
the following modified notion of congruence.
Let N be a positive integer and consider distinct
weight 2 newforms f and g whose levels Nf and Ngboth divide N. Denote by
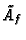 the abelian
variety generated by the images of Af in J0(N)under the degeneracy maps, and similarly define
the abelian
variety generated by the images of Af in J0(N)under the degeneracy maps, and similarly define
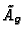 .
We say that f and g are congruent at level N modulo a
rational prime p, written
.
We say that f and g are congruent at level N modulo a
rational prime p, written
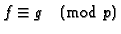 ,
if p divides
the order of the finite group
,
if p divides
the order of the finite group
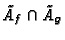 .
Deciding whether or not f and g are congruent can be
accomplished by working in the integral homology
H1(X0(N),Z)using the algorithm of Section
.
Deciding whether or not f and g are congruent can be
accomplished by working in the integral homology
H1(X0(N),Z)using the algorithm of Section ![[*]](cross_ref_motif.gif) .
.
William A. Stein
1999-08-31
![[*]](cross_ref_motif.gif) .
.