Theorem 3.1
Let
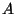
and
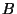
be abelian subvarieties of an abelian
variety
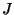
over a number field
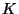
such that
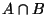
is finite.
Let
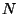
be an integer divisible by the residue characteristics
of primes of bad reduction for
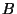
.
Suppose
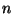
is an integer such that for each prime
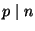
,
we have
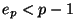
where
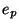
is
the largest ramification of any
prime of
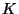
lying over
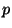
, and that
where
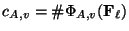
(resp.,
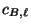
) is
the Tamagawa number of
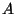
(resp.,
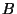
)
at
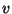
(see Section
3.1 for the definition
of
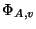
). Suppose furthermore that
![$ B[n] \subset A$](img98.png)
as subgroup schemes of
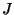
.
Then there is a natural map
such that
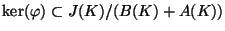
.
If
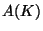
has rank 0, then
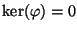
(more generally,
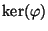
has order at
most
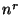
where
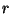
is the rank of
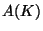
).
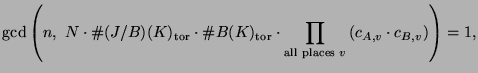
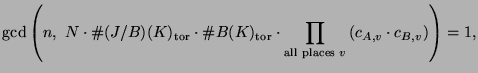
![]() th root of an unramified point. In
Section 3.3, we use the snake lemma to produce a map
th root of an unramified point. In
Section 3.3, we use the snake lemma to produce a map