Next: Strong Visibility at Higher Up: Equivariant Visibility Previous: Some commutative algebra
where
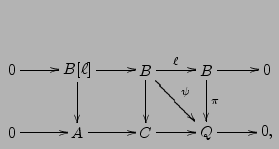 is the composition of the inclusion
is the composition of the inclusion
Here,
 ,
, The snake lemma yields an exact sequence
By hypothesis,
By the long exact sequence on Galois cohomology,
the quotient ![]() is isomorphic to a subgroup of
is isomorphic to a subgroup of ![]() and by hypothesis
and by hypothesis
![]() , so
, so
![]() .
Since
.
Since ![]() is isogenous to
is isogenous to ![]() and
and ![]() is finite
and
is finite
and
![]() , we see that
, we see that
![]() is finite. Thus
is finite. Thus ![]() is a quotient
of the finite
is a quotient
of the finite ![]() -module
-module ![]() , which has no
, which has no
![]() -torsion, so Lemma 4.2.2 implies
that
-torsion, so Lemma 4.2.2 implies
that
![]() . The same lemma
implies that
. The same lemma
implies that ![]() has no
has no
![]() -torsion,
since it is a quotient of the finite module
-torsion,
since it is a quotient of the finite module
![]() , which has no
, which has no
![]() -torsion. Thus, we
have an exact sequence
-torsion. Thus, we
have an exact sequence
and both of
It remains to show that for any
![]() , we have
, we have
![]() , i.e., that
, i.e., that
![]() is locally trivial.
is locally trivial.
For real archimedian places tex2html_wrap_inline$v$ the cohomology group tex2html_wrap_inline$H^1(K_v/K_v,A)$ is trivial. For complex archimedian places, every cohomology class has order 2 since tex2html_wrap_inline$Gal(K_v/K) &cong#cong;Gal(C/R) &cong#cong;Z/2Z$ and the order of any cohomology class divides the order of the group []. Since tex2html_wrap_inline$res_v(&phiv#varphi;(&pi#pi;(x)))$ is also tex2html_wrap_inline$&ell#ell;$-torsion and tex2html_wrap_inline$&ell#ell;$ is odd (since tex2html_wrap_inline$1&le#leq;e < &ell#ell;- 1$), then tex2html_wrap_inline$res_v(&phiv#varphi;(&pi#pi;(x))) = 0$.
Let tex2html_wrap_inline$v$ be a non-archimedian place for which chartex2html_wrap_inline$(v) &ne#ne;&ell#ell;$. If
tex2html_wrap_inline$m = c_B,v$ denotes the Tamagawa number at tex2html_wrap_inline$v$ for tex2html_wrap_inline$B$, then the
reduction of tex2html_wrap_inline$mx$ lands in the identity component of the closed fiber
of the Néron model of tex2html_wrap_inline$B$. The field tex2html_wrap_inline$K_v^ur$ is
the fraction field of a strictly Henselian discrete valuation ring, so
we can apply Proposition ![]() to obtain a point
tex2html_wrap_inline$z &isin#in;B(K^ur_v)$, such that tex2html_wrap_inline$mx = &ell#ell;z$. The cohomology class
tex2html_wrap_inline$res_v(&pi#pi;(mx))$ is represented by the 1-cocycle
tex2html_wrap_inline$&xi#xi;: Gal(K_v/K_v) &rarr#rightarrow;A(K_v^ur )$, given by
tex2html_wrap_inline$&sigma#sigma;&map#mapsto;&sigma#sigma;(z)-z &isin#in;A(K_v^ur)$. It follows that tex2html_wrap_inline$[&xi#xi;]$
is an unramified cohomology class, i.e., tex2html_wrap_inline$[&xi#xi;] &isin#in;
H^1(K_v^ur / K_v ,A(K_v^ur))$, i.e., tex2html_wrap_inline$res_v(&pi#pi;(mx))$ is unramified.
to obtain a point
tex2html_wrap_inline$z &isin#in;B(K^ur_v)$, such that tex2html_wrap_inline$mx = &ell#ell;z$. The cohomology class
tex2html_wrap_inline$res_v(&pi#pi;(mx))$ is represented by the 1-cocycle
tex2html_wrap_inline$&xi#xi;: Gal(K_v/K_v) &rarr#rightarrow;A(K_v^ur )$, given by
tex2html_wrap_inline$&sigma#sigma;&map#mapsto;&sigma#sigma;(z)-z &isin#in;A(K_v^ur)$. It follows that tex2html_wrap_inline$[&xi#xi;]$
is an unramified cohomology class, i.e., tex2html_wrap_inline$[&xi#xi;] &isin#in;
H^1(K_v^ur / K_v ,A(K_v^ur))$, i.e., tex2html_wrap_inline$res_v(&pi#pi;(mx))$ is unramified.
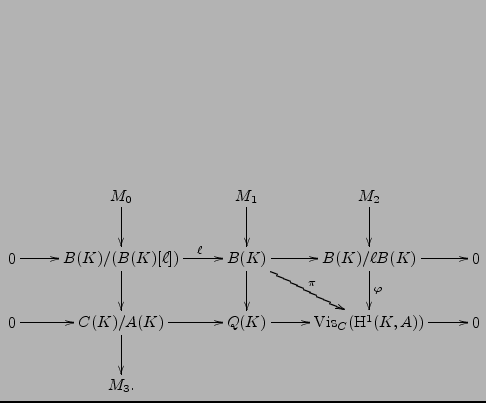
We proceed exactly as in Section 3.5 of [AS05].
In both cases
char![]() and
char
and
char![]() we
arrive at the conclusion that the restriction
of
we
arrive at the conclusion that the restriction
of
![]() to
to
![]() is an element
is an element
![]() .
(Note that in the case
char
.
(Note that in the case
char![]() the proof
uses our hypothesis that
the proof
uses our hypothesis that
![]() .)
By [Mil86, Prop I.3.8], there is an
isomorphism
.)
By [Mil86, Prop I.3.8], there is an
isomorphism
We will use our hypothesis that
for all
where
Lemma 4.2.5, our hypothesis that
together imply that
William Stein 2006-06-21