Next: Bibliography Up: Conjecture, evidence and more Previous: Visibility of Kolyvagin cohomology
|
|
dim |
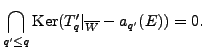
|
moddeg | |
| 551H | 18 | 3 |
|
(2, 1102A1, -) |
| 767E | 23 | 3 | |
(2, 1534B1, 3) |
| 959D | 24 | 3 |
|
(2, 1918C1, 5), (7, 5369A1,2) |
| 1337E | 33 | 3 |
|
(2, 2674A1, 5) |
| 1339G | 30 | 3 |
|
(2, 2678B1, 3), (11, 14729A1,2) |
William Stein 2006-06-21