Visibility of Kolyvagin cohomology classes

It would also be interesting to study visibility at higher level of Kolyvagin cohomology classes. The following is a first ``test question'' in this direction.

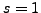
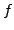
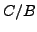
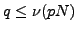
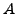
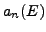
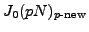
Question 7.3.1   Suppose $E\subset J_0(N)$ is an elliptic curve with conductor $N$ , and fix a prime $\ell$ such that $\overline{\rho}_{E,\ell}$ is surjective. Fix a quadratic imaginary field $K$ that satisfies the Heegner hypothesis for $E$ . For any prime $p$ satisfying the conditions of [Rub89, Prop. 5], let $c_{p} \in \H ^1(\mathbb{Q},E)[\ell]$ be the corresponding Kolyvagin cohomology class. There are two natural homomorphisms $\delta_1^*, \delta_p^*:E \to J_0(Np)$ . 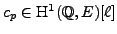When is

$$(\delta_1^* \pm \delta_\ell^*)_*(c_\ell) = 0 \in \H ^1(\mathbb{Q},J_0(Np))?$$

When is

$${\mathrm{res}}_v((\delta_1^* \pm \delta_\ell^*)_*(c_\ell)) = 0 \in \H ^1(\mathbb{Q}_v,J_0(Np))?$$