Next: Level 959 Up: Computational Examples Previous: Computational Examples
We first show that the Birch and Swinnerton-Dyer conjectural formula predicts that the orders of
the groups
![]() and
and
![]() are both divisible by 9.
are both divisible by 9.
Next, we use [AS05, §4] to compute the ratio of the special value of the
![]() -function of
-function of
![]() at 1 over the real Néron period
at 1 over the real Néron period
![]() . We obtain
. We obtain
![]() , where
, where
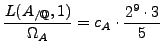 is the Manin constant.
Since
is the Manin constant.
Since
![]() by [ARS06] then
by [ARS06] then
for some
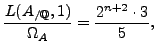 . In particular, the modular abelian variety
. In particular, the modular abelian variety
Next, using the algorithms from [CS01,KS00] we compute the Tamagawa
number
![]() . We also find that
. We also find that
![]() is a power
of
is a power
of ![]() because
because ![]() acts as
acts as ![]() on
on ![]() , and on the component
group
, and on the component
group
![]() , so the fixed subgroup
, so the fixed subgroup
![]() of Frobenius
is a
of Frobenius
is a ![]() -group (for more details, see [Rib90a, Prop. 3.7-8]).
-group (for more details, see [Rib90a, Prop. 3.7-8]).
Finally, the Birch and Swinnerton-Dyer conjectural formula for abelian varieties of Mordell-Weil rank zero (see [AS05, Conj. 2.2]) asserts that
By substituting what we computed above, we obtain
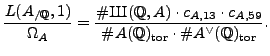 .
Since
.
Since
We next observe that there are no visible elements of odd order for the embedding
![]() .
.
Finally, we use Theorem 5.4.2 to prove the existence of non-trivial elements of order 3
in
![]() which are invisible at level
which are invisible at level ![]() , but become visible at higher level.
In particular, we prove unconditionally that
, but become visible at higher level.
In particular, we prove unconditionally that
![]() which provides evidence for
the Birch and Swinnerton-Dyer conjectural formula.
which provides evidence for
the Birch and Swinnerton-Dyer conjectural formula.
has conductor
We apply Theorem 5.4.2 with
We have
![]() . Using Magma we find
. Using Magma we find
which verifies the noncongruence hypothesis and completes the proof.
![]()
William Stein 2006-06-21