Component Groups of Purely Toric Quotients

William A. Stein - Brian Conrad

Abstract:

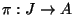
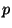
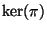
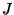
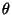
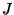
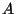
Suppose $\pi:J\rightarrow A$ is an optimal quotient of abelian varieties over a $p$-adic field, optimal in the sense that $\ker(\pi)$ is connected. Assume that $J$ is equipped with a symmetric principal polarization $\theta$ (e.g., any Jacobian of a curve has such a polarization), that $J$ has semistable reduction, and that $A$ has purely toric reduction. 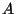In this paper, we express the group of connected components of the Néron model of $A$ in terms of the monodromy pairing on the character group of the torus associated to $J$. 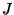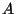We apply our results in the case when $A$ is an optimal quotient of the modular Jacobian $J_0(N)$. 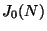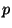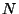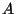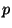For each prime $p$ that exactly divides $N$, we obtain an algorithm to compute the component group of $A$ at $p$.