


Next: Newforms and Optimal Quotients
Up: Optimal Quotients of
Previous: Optimal Quotients of
Let 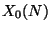 be the modular curve
associated to the subgroup
be the modular curve
associated to the subgroup
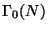 of
of
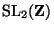 that consists of those matrices which are upper
triangular modulo
that consists of those matrices which are upper
triangular modulo 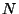 . The algebraic curve
. The algebraic curve
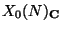 can be constructed as
a Riemann surface as the quotient
and
can be constructed as
a Riemann surface as the quotient
and 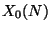 has a canonical structure of algebraic curve over
has a canonical structure of algebraic curve over
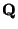 .
.
It is well known that the 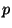 -new part of
the Jacobian
-new part of
the Jacobian 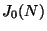 of
of 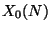 has purely
toric reduction at
has purely
toric reduction at 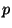 when
when
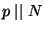 .
Let us briefly recall the reason, writing
.
Let us briefly recall the reason, writing 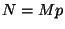 .
Using the description of closed fibers of modular curves
[10, Ch. 13] and Raynaud's result relating Néron
models and Picard functors (as summarized in [2, Ch. 9]),
the standard finite flat degeneracy maps
.
Using the description of closed fibers of modular curves
[10, Ch. 13] and Raynaud's result relating Néron
models and Picard functors (as summarized in [2, Ch. 9]),
the standard finite flat degeneracy maps
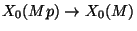 over
over
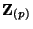 induce a ``pushfoward'' map
on Néron model connected components
induce a ``pushfoward'' map
on Néron model connected components
which on the closed fiber is the map induced by
pullback to the two components
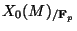 in
in
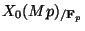 .
The kernel of this latter map is a torus [2, Ex. 9.2.8],
yet this kernel is visibly isogenous to the semistable mod
.
The kernel of this latter map is a torus [2, Ex. 9.2.8],
yet this kernel is visibly isogenous to the semistable mod 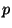 fiber of the dual of
fiber of the dual of
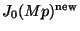 , whence the purely toric
conclusion.
, whence the purely toric
conclusion.



Next: Newforms and Optimal Quotients
Up: Optimal Quotients of
Previous: Optimal Quotients of
William A Stein
2001-12-09
![]() -new part of
the Jacobian
-new part of
the Jacobian ![]() of
of ![]() has purely
toric reduction at
has purely
toric reduction at ![]() when
when
![]() .
Let us briefly recall the reason, writing
.
Let us briefly recall the reason, writing ![]() .
Using the description of closed fibers of modular curves
[10, Ch. 13] and Raynaud's result relating Néron
models and Picard functors (as summarized in [2, Ch. 9]),
the standard finite flat degeneracy maps
.
Using the description of closed fibers of modular curves
[10, Ch. 13] and Raynaud's result relating Néron
models and Picard functors (as summarized in [2, Ch. 9]),
the standard finite flat degeneracy maps
![]() over
over
![]() induce a ``pushfoward'' map
on Néron model connected components
induce a ``pushfoward'' map
on Néron model connected components