Lemma 5.2
Suppose that
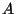
is a purely toric abelian variety over
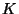
and that
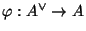
is a symmetric isogeny.
Let
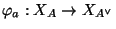
denote the induced map on character
groups. Then
Proof.
By Corollary
8.7 applied to our isogeny
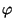
(so what we are presently calling
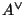
and
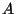
are respectively called
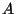
and
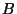
in the discussion
surrounding Theorem
8.6), we deduce that
where
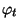
and
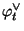
are the maps induced by
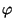
and
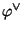
on closed fiber tori.
Since the character
group 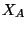 is, by definition,
is, by definition,
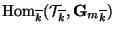 , where
, where
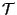 is the
toric part of the closed fiber of
is the
toric part of the closed fiber of 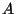 , it follows that
, it follows that
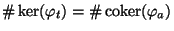 .
Since
.
Since
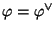 , this proves the lemma.
, this proves the lemma.

![]() is, by definition,
is, by definition,
![]() , where
, where
![]() is the
toric part of the closed fiber of
is the
toric part of the closed fiber of ![]() , it follows that
, it follows that
![]() .
Since
.
Since
![]() , this proves the lemma.
, this proves the lemma.
![]()