


Next: Fermat's Little Theorem
Up: Lecture 5: Congruences
Previous: Rules for Divisibility
Definition 3.1 (Complete Set of Residues)
A
complete set of residues modulo
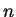
is a subset
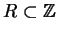
of size
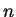
whose reductions modulo
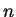
are distinct. In other words,
a complete set of residues is a choice of representive for each
equivalence class in
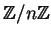
.
Some examples:
is a complete set of residues modulo 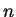 .
When
.
When 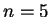 , a complete set of residues is
, a complete set of residues is
Lemma 3.2
If
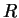
is a complete set of residues modulo
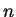
and
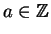
with
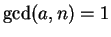
, then
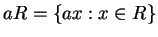
is also a complete set of residues.
Proof.
If
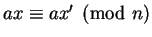
with
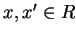
, then
Proposition
2.1 implies that
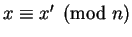
.
Because
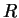
is a complete set of residues, this implies
that
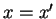
. Thus the elements of
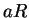
have distinct reductions modulo
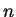
.
It follows, since
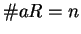
, that
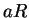
is a
complete set of residues modulo
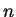
.

Definition 3.3 (Linear Congruence)
A
linear congruence is an equation of the form
Proposition 3.4
If
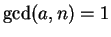
, then the equation
must have a solution.
Proof.
Let
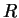
be a complete set of residues modulo
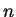
(for
example,
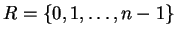
).
Then by Lemma
3.2,
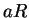
is also a complete set of residues.
Thus there is an element
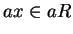
such
that
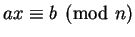
, which proves
the proposition.

The point in the proof is that left multiplication by 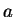 defines
a map
defines
a map
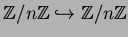 , which must be surjective
because
, which must be surjective
because
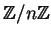 is finite.
is finite.
Illustration:
Set
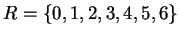 .
Then
so
.
Then
so
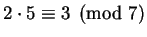 .
.
Warning:
Note that the equation
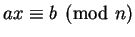 might have a solution even if
might have a solution even if
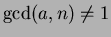 . To construct
such examples, let
. To construct
such examples, let 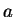 be any divisor of
be any divisor of 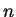 ,
, 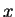 any number, and set
any number, and set 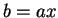 .
For example,
.
For example,
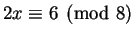 has a solution!
has a solution!



Next: Fermat's Little Theorem
Up: Lecture 5: Congruences
Previous: Rules for Divisibility
William A Stein
2001-09-20
![]() might have a solution even if
might have a solution even if
![]() . To construct
such examples, let
. To construct
such examples, let ![]() be any divisor of
be any divisor of ![]() ,
, ![]() any number, and set
any number, and set ![]() .
For example,
.
For example,
![]() has a solution!
has a solution!