A Simple Bound

The following elementary lemma, which the second author learned from Hendrik Lenstra, will be used to give a bound on the visibility dimension in terms of the order of $c$ and the dimension of $A$.

Lemma 2.2   Let $G$ be a group,  $M$ be a finite (discrete) $G$-module, and $c \in H^1(G,M)$. Then there is a subgroup $H$ of $G$ such that $\res_H(c)=0$ and $\char93 (G/H) \leq \char93 M$.

Proof. Let $f:G \rightarrow M$ be a cocycle corresponding to $c$, so $f(\tau\sigma) = f(\tau) + \tau f(\sigma)$ for all $\tau, \sigma\in G$. Let $H = \ker(f) = \{\sigma \in G : f(\sigma) = 0\}$. The map $\tau H \mapsto f(\tau)$ is a well-defined injection from the coset space $G/H$ to $M$. $\qedsymbol$

The following is a general bound on the visibility dimension.

Proposition 2.3   The visibility dimension of any  $c\in H^1(K,A)$ is at most $d\cdot{}n^{2d}$ where $n$ is the order of $c$ and $d$ is the dimension of $A$.

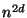
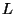
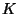
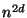
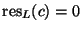
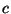
Proof. The map $H^1(K,A[n])\rightarrow H^1(K,A)[n]$ is surjective and $A[n]$ has order $n^{2d}$, so Lemma 2.2 implies that there is an extension $L$ of $K$ of degree at most $n^{2d}$ such that $\res_L(c)=0$. The proof of Proposition 1.3 implies that $c$ is visible in an abelian variety of dimension $[L:K]\cdot \dim A\leq d n^{2d}$. $\qedsymbol$