


Next: Simplest Case: 1 variable
Up: Freshman Seminar 21n: Elliptic
Previous: Reading
Number Theory is mainly about relations between rational
numbers (fractions, which are denoted 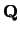 ).
).
Examples:
- Every positive integer can be written in a unique
way (up to order) as a product of primes.
- The equation
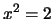 has no solution with
has no solution with
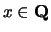 .
.
- The equation
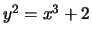 has infinitely many solutions
has infinitely many solutions
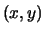 with
with
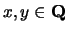 . E.g.,
. E.g.,
(In a few weeks you'll know how I found such big solutions.)
Much of number theory involves finding integer or rational
solutions to polynomial equations. After all, solutions to such
equations are relations between numbers.
Subsections
William A Stein
2003-02-03
![]() ).
).