


Next: Pep Talk
Up: Freshman Seminar 21n: Elliptic
Previous: Some Math Problems
Read pages 1-15 of Silverman-Tate. Try each of the following
problems, but be able to present a solution to the one with your name
next to it:
- (Jeff) Prove that the line connecting two distinct rational points in the
plane is defined by an equation
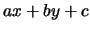 with
with
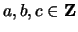 , then
prove that the intersection of any two distinct rational lines in the
plane is empty or a single rational point.
, then
prove that the intersection of any two distinct rational lines in the
plane is empty or a single rational point.
- (Jennifer) Find all right triangles with integer side lengths
and hypotenuse
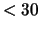 .
.
- (Mauro) For each of the following conics, either find five rational
points or prove that there are no rational points:
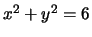
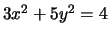
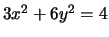
- (Alex) Draw a rough graph of the conic
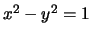 , then give
a formula for all the rational points on this conic.
, then give
a formula for all the rational points on this conic.
- (Jenna) Use induction on
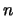 to
prove that for every
to
prove that for every 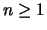 , the congruence
, the congruence
has a solution
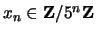 .
.
William A Stein
2003-02-03