Lenstra's algorithm is well suited for finding ``medium sized''
factors of an integer 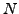 , which today means between
, which today means between 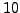 to
to 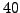 decimal
digits. The ECM method is not directly used for factoring
RSA challenge numbers (see Section 1.1.3), but it is
used on auxiliary numbers as a crucial step in the ``number field
sieve'', which is the best known algorithm for hunting for such
factorizations. Also, implementation of ECM typically requires little
memory.
decimal
digits. The ECM method is not directly used for factoring
RSA challenge numbers (see Section 1.1.3), but it is
used on auxiliary numbers as a crucial step in the ``number field
sieve'', which is the best known algorithm for hunting for such
factorizations. Also, implementation of ECM typically requires little
memory.
|
![\includegraphics[width=\textwidth]{graphics/lenstra.eps}](img2109.png)