Fix a positive integer 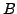 . If
. If 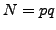 with
with 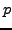 and
and 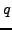 prime and
prime and
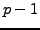 and
and 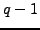 are not
are not 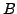 -power smooth, then
the Pollard
-power smooth, then
the Pollard 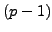 -method is unlikely to work.
For example, let
-method is unlikely to work.
For example, let 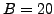 and
suppose that
and
suppose that
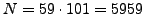 . Note that
neither
. Note that
neither
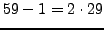 nor
nor
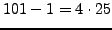 is
is 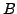 -power smooth.
With
-power smooth.
With
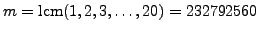 , we have
, we have
and
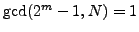 , so we do not find a factor of
, so we do not find a factor of 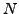 .
.
As remarked above, the problem is that 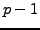 is not
is not 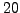 -power smooth for
either
-power smooth for
either 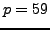 or
or 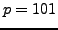 . However, notice that
. However, notice that
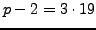 is
is
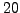 -power smooth. Lenstra's ECM replaces
-power smooth. Lenstra's ECM replaces
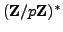 , which has order
, which has order 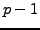 , by the group of points
on an elliptic curve
, by the group of points
on an elliptic curve 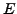 over
over
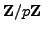 .
It is a theorem that
.
It is a theorem that
for some nonnegative integer
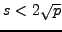 (see e.g., [#!silverman:aec!#, §V.1] for a proof).
(Also every value of
(see e.g., [#!silverman:aec!#, §V.1] for a proof).
(Also every value of 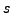 subject to this
bound occurs, as one can see using ``complex multiplication
theory''.) For example, if
subject to this
bound occurs, as one can see using ``complex multiplication
theory''.) For example, if 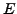 is the elliptic curve
is the elliptic curve
over
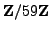 then by enumerating points one sees that
then by enumerating points one sees that
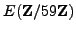 is cyclic of order
is cyclic of order 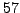 . The set of numbers
. The set of numbers 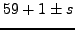 for
for 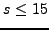 contains
contains 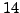 numbers that are
numbers that are 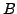 -power smooth
for
-power smooth
for 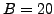 .Thus working with an elliptic curve gives us more flexibility.
For example,
.Thus working with an elliptic curve gives us more flexibility.
For example, 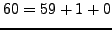 is
is 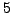 -power smooth and
-power smooth and
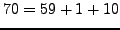 is
is
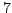 -power smooth.
-power smooth.
William
2007-06-01
![]() is not
is not ![]() -power smooth for
either
-power smooth for
either ![]() or
or ![]() . However, notice that
. However, notice that
![]() is
is
![]() -power smooth. Lenstra's ECM replaces
-power smooth. Lenstra's ECM replaces
![]() , which has order
, which has order ![]() , by the group of points
on an elliptic curve
, by the group of points
on an elliptic curve ![]() over
over
![]() .
It is a theorem that
.
It is a theorem that