Next: Proof of Quadratic Reciprocity Up: First Proof of Quadratic Previous: First Proof of Quadratic Contents Index
be the set of integers between
and
provided that each interval involved in the congruence is nonempty.
where the union is disjoint. There are
in the interval
and
Once we have proved the following proposition, it will be easy to deduce the quadratic reciprocity law.
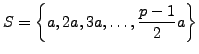
and
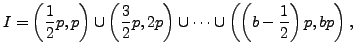
where
We check that every element of ![]() that is equivalent modulo
that is equivalent modulo ![]() to something in the
interval
to something in the
interval
![]() lies in
lies in ![]() .
First suppose that
.
First suppose that
![]() . Then
. Then
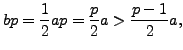
so each element of
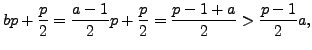
so
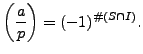
To compute
![]() , first rescale by
, first rescale by ![]() to see that
to see that
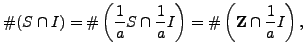
where
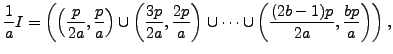
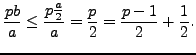
Write ![]() , and let
, and let
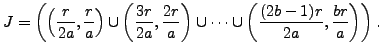
The only difference between
By Lemma 4.3.3,
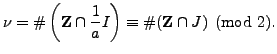
Thus
If
![]() , then the only change in the above computation
is that
, then the only change in the above computation
is that ![]() is replaced by
is replaced by ![]() . This changes
. This changes ![]() into
into
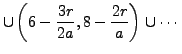 |
||
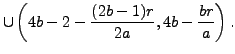 |
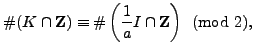
so
The following more careful analysis in the special case when ![]() helps illustrate the proof of the above lemma, and the result is
frequently useful in computations. For an alternative proof
of the proposition, see Exercise 4.6.
helps illustrate the proof of the above lemma, and the result is
frequently useful in computations. For an alternative proof
of the proposition, see Exercise 4.6.
We must count the parity of the number of elements of
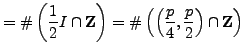 |
||
William 2007-06-01