The Chinese Remainder Theorem
In this section we prove the Chinese Remainder Theorem, which gives
conditions under which a system of linear equations is guaranteed to
have a solution.
In the 4th century a Chinese mathematician asked the following:
Question 2.2
There is a quantity whose number is unknown. Repeatedly divided
by 3, the remainder is 2; by 5 the remainder is 3; and by 7 the
remainder is 2. What is the quantity?
In modern notation, Question 2.2.1 asks us to
find a positive integer solution to the following system of
three equations:
The Chinese Remainder Theorem asserts that a solution
exists, and the proof gives a method to find one.
(See Section 2.3 for the necessary algorithms.)
Proof.
Since
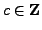
, we have
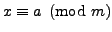
,
and using that
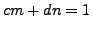
, we have
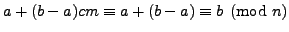
.

Now we can answer Question 2.2.1.
First, we use Theorem 2.2.2
to find a solution to the pair of equations
Set 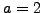 ,
, 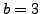 ,
, 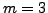 ,
, 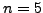 .
Step 1 is to find a solution to
.
Step 1 is to find a solution to
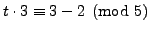 .
A solution is
.
A solution is 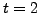 . Then
. Then
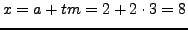 .
Since any
.
Since any 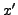 with
with
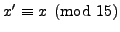 is also a solution to
those two equations, we can solve all three equations by
finding a solution to the pair of equations
is also a solution to
those two equations, we can solve all three equations by
finding a solution to the pair of equations
Again, we find a solution to
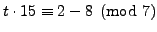 .
A solution is
.
A solution is 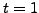 , so
, so
Note that there are other solutions. Any
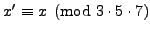 is also a solution; e.g.,
is also a solution; e.g.,
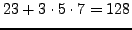 .
.
SAGE Example 2.2
The SAGE command CRT(a,b,m,n) computes an integer
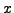
such that
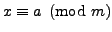
and
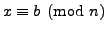
. For example,
sage: CRT(2,3, 3, 5)
8
The CRT_list command computes a number that reduces to
several numbers modulo coprime modulo. We use
it to answer Question
2.2.1:
sage: CRT_list([2,3,2], [3,5,7])
23
Subsections
William
2007-06-01
![]() and
and ![]() solve both congruences. Then
solve both congruences. Then
![]() satisfies
satisfies
![]() and
and
![]() , so
, so ![]() and
and ![]() . Since
. Since
![]() , it follows that
, it follows that ![]() , so
, so
![]() .
.
![]()