Suppose
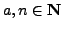 with
with
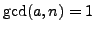 . Then
by Proposition 2.1.12
the equation
. Then
by Proposition 2.1.12
the equation
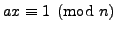 has a unique solution.
How can we find it?
has a unique solution.
How can we find it?
Proposition 2.3 (Extended Euclidean representation)
Suppose
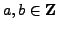 and let
and let
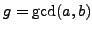 . Then
there exists
. Then
there exists
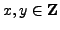 such that
such that
Remark 2.3
If
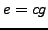
is a multiple of
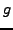
, then
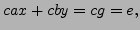
so
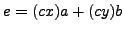
can
also be written in terms of
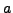
and
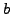
.
Proof.
[Proof of Proposition
2.3.1]
Let
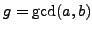
. Then
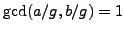
, so by Proposition
2.1.14 the equation
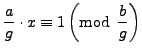 |
(2.3.1) |
has a solution
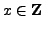
. Multiplying (
2.3.1) through by
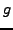
yields
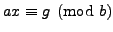
, so there exists
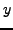
such that
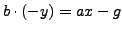
. Then
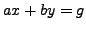
, as required.

Given 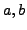 and
and
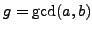 , our proof of
Proposition 2.3.1 gives a way to explicitly find
, our proof of
Proposition 2.3.1 gives a way to explicitly find 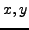 such
that
such
that 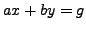 , assuming one knows an algorithm to solve linear
equations modulo
, assuming one knows an algorithm to solve linear
equations modulo  . Since we do not know such an algorithm, we now
discuss a way to explicitly find
. Since we do not know such an algorithm, we now
discuss a way to explicitly find 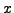 and
and 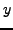 . This algorithm
will in fact enable us to solve linear equations modulo
. This algorithm
will in fact enable us to solve linear equations modulo  --to solve
--to solve
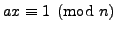 when
when
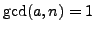 , use the algorithm below to
find
, use the algorithm below to
find 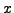 and
and 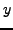 such that
such that 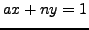 . Then
. Then
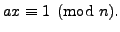
Example 2.3
Suppose
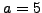
and
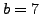
. The steps of Algorithm
1.1.13 to
compute
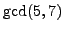
are, as follows. Here we underline certain
numbers, because it clarifies the subsequent back substitution we
will use to find
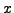
and
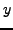
.
On the right, we have back-substituted in order to write each partial
remainder as a linear combination of
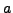
and
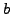
. In the last step,
we obtain
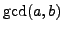
as a linear combination of
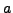
and
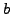
, as
desired.
Example 2.3
That example was not too complicated, so we try another one.
Let
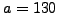
and
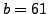
. We have
Thus
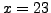
and
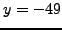
is a solution to
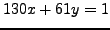
.
Example 2.3
This example is just like Example
2.3.4 above,
except we make the notation on the right more compact.
Notice at each step that the vector on the right is just the vector from
two steps ago minus a multiple of the vector from one step ago, where
the multiple is the cofficient of what we divide by.
SAGE Example 2.3
The SAGE command xgcd(a,b) computes the greatest common
divisor
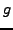
of
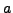
and
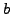
along with
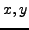
such that
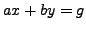
.
sage: xgcd(5,7)
(1, 3, -2)
sage: xgcd(130,61)
(1, 23, -49)
Proof.
This algorithm is the same as Algorithm
1.1.13, except that we
keep track of extra variables
, so it terminates and when
it terminates
.
We omit the rest of the inductive proof that the algorithm
is correct, and instead refer the reader to
[#!knuth1!#, §1.2.1] which contains a detailed proof
in the context of a discussion of how one
writes mathematical proofs.

Proof.
Reduce
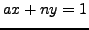
modulo

to see that
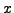
satisfies
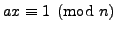
.

Example 2.3
Solve
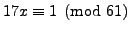
.
First, we use Algorithm
2.3.7 to find
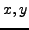
such that
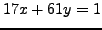
:
Thus
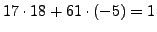
so
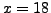
is a solution to
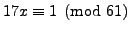
.
SAGE Example 2.3
SAGE implements the above algorithm for quickly
computing inverses modulo

. For example,
sage: a = Mod(17, 61)
sage: a^(-1)
18
William
2007-06-01
![]() and
and
![]() , our proof of
Proposition 2.3.1 gives a way to explicitly find
, our proof of
Proposition 2.3.1 gives a way to explicitly find ![]() such
that
such
that ![]() , assuming one knows an algorithm to solve linear
equations modulo
, assuming one knows an algorithm to solve linear
equations modulo ![]() . Since we do not know such an algorithm, we now
discuss a way to explicitly find
. Since we do not know such an algorithm, we now
discuss a way to explicitly find ![]() and
and ![]() . This algorithm
will in fact enable us to solve linear equations modulo
. This algorithm
will in fact enable us to solve linear equations modulo ![]() --to solve
--to solve
![]() when
when
![]() , use the algorithm below to
find
, use the algorithm below to
find ![]() and
and ![]() such that
such that ![]() . Then
. Then
![]()