A Related Sequence of Integrals

Now, we define a sequence of real numbers $T_0, T_1, T_2, \ldots$ by the following integrals:

$$T_n=\int_{0}^{1}\frac{t^{n}(t-1)^{n}}{n!}\phantom{1} e^tdt.$$

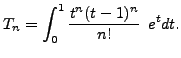
Below, we compute the first two terms of this sequence explicitly. (When we compute $T_1$ , we are doing the integration by parts $u=t(t-1)$ , $dv=e^tdt$ . Since the integral runs from 0 to 1, the boundary condition is 0 when evaluated at each of the endpoints. This vanishing will be helpful when we do the integral in the general case.)

$$T_0 =\int_{0}^{1}e^tdt=e-1,$$

$$T_1 =\int_{0}^{1}t(t-1)e^tdt$$

$$=-\int_{0}^{1}((t-1)+t)e^tdt$$

$$=-(t-1)e^t\Bigg\vert _0^{1}-te^t\Bigg\vert _0^{1}+2\int_{0}^{1}e^tdt$$

$$=-1-e+2(e-1)=e-3.$$

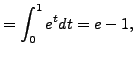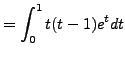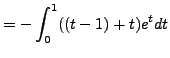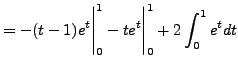The reason that we defined this series now becomes apparent: $T_0=y_0e-x_0$ and that $T_1=y_1e-x_1$ . In general, it will be true that $T_n=y_ne-x_n$ . We will now prove this fact.

It is clear that if the $T_n$ were to satisfy the same recurrence that the $x_i$ and $y_i$ do, in equation (5.3.1), then the above statement holds by induction. (The initial conditions are correct, as needed.) So we simplify $T_n$ by integrating by parts twice in succession:

$$T_n =\int_{0}^{1}\frac{t^{n}(t-1)^{n}}{n!}\phantom{1} e^tdt$$

$$=-\int_{0}^{1}\frac{t^{n-1}(t-1)^{n}+t^{n}(t-1)^{n-1}}{(n-1)!}\phantom{1} e^tdt$$

$$=\int_{0}^{1}\Bigl(\frac{t^{n-2}(t-1)^{n}}{(n-2)!}+n\frac{t^{n-1}(t-1)^{n-1}}{(n-1)!}$$

$$\qquad\qquad\qquad + n\frac{t^{n-1}(t-1)^{n-1}}{(n-1)!}+\frac{t^{n}(t-1)^{n-2}}{(n-2)!}\Bigr)e^tdt$$

$$=2nT_{n-1}+\int_{0}^{1}\frac{t^{n-2}(t-1)^{n-2}}{n-2!}(2t^2-2t+1)\phantom{1} e^tdt$$

$$=2nT_{n-1}+2\int_{0}^{1}\frac{t^{n-1}(t-1)^{n-1}}{n-2!}\phantom{1} e^tdt+\int_{0}^{1}\frac{t^{n-2}(t-1)^{n-2}}{n-2!}\phantom{1} e^tdt$$

$$=2nT_{n-1}+2(n-1)T_{n-1}+T_{n-2}$$

$$=2(2n-1)T_{n-1}+T_{n-2},$$

which is the desired recurrence.

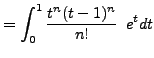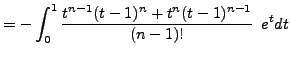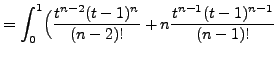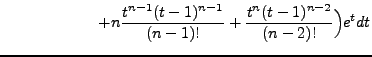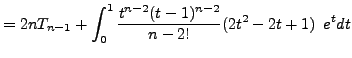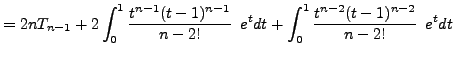Therefore $T_n=y_ne-x_n$ . To conclude the proof, we consider the limit as $n$ approaches infinity:

$$\lim_{n \to \infty}\int_{0}^{1}\frac{t^{n}(t-1)^{n}}{n!}\phantom{1} e^tdt=0,$$

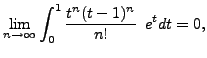
by inspection, and therefore

$$\lim_{n \to \infty}\frac{x_n}{y_n}=\lim_{n \to \infty}(e-\frac{T_n}{y_n})=e.$$

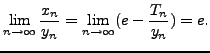
Therefore, the ratio $x_n/y_n$ approaches $e$ , and the continued fraction expansion $[2,1,2,1,1,4,1,1,\ldots]$ does in fact converge to $e$ .