


Next: A Conjecture About Nonvanishing
Up: NONVANISHING TWISTS AND VISIBLE
Previous: Terminology
Visibility theory has been developed by Barry Mazur, Amod Agashe,
and myself, with periodic help from Brian Conrad.
Let
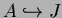 be a closed immersion of abelian varieties.
Then
be a closed immersion of abelian varieties.
Then
Theorem 2.1
Suppose
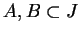
, and
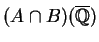
is finite.
If
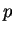
is a prime such that
![$ B[p]\subset A$](img17.png)
and
then
For the proof, look at [Agashe-Stein, Visibility of
Shafarevich-Tate Groups of Abelian Varieties].
It uses the snake lemma, and a careful local analysis at
each prime that uses standard arithmetic geometry tools.
William A Stein
2001-10-01
![]() be a closed immersion of abelian varieties.
Then
be a closed immersion of abelian varieties.
Then