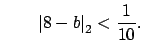The following theorem asserts that inequivalent valuations are in fact
almost totally indepedent. For our purposes it will be superseded by
the strong approximation theorem (Theorem 20.4.4).
Proof.
We note first that it will be enough to find, for each
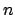
, an
element
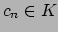
such that
where
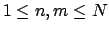
. For then as
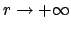
, we have
It is then enough to take
By symmetry it is enough to show the existence of 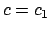 with
with
We will do this by induction on
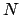
.
First suppose  . Since
. Since
 and
and
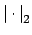 are
inequivalent (and all absolute values are assumed nontrivial)
there is an
are
inequivalent (and all absolute values are assumed nontrivial)
there is an  such that
such that
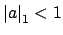 and and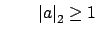 |
(16.2) |
and similarly a
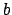
such that
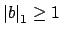
and
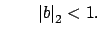
Then
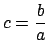
will do.
Remark 16.3.2
It is not completely clear that
one can choose an
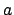
such that (
16.3.1) is satisfied.
Suppose it were impossible. Then because the valuations are
nontrivial, we would have that for any

if

then
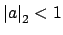
. This implies the converse statement: if

and
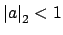
then

. To see this, suppose there
is an

such that
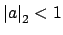
and
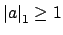
.
Choose
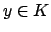
such that
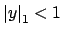
. Then for any integer
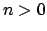
we have
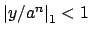
, so by hypothesis
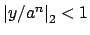
. Thus
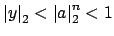
for all
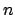
. Since
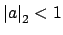
we
have

as
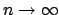
, so

, a
contradiction since

. Thus

if and only if
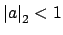
, and we have proved before that this implies that

is equivalent to
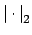
.
Next suppose 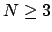 . By the case
. By the case 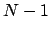 , there is an
, there is an  such
that
such
that
By the case for

there is a
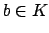
such that

and
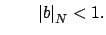
Then put
where
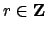
is sufficiently large so that
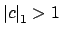
and
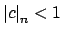
for

.

Example 16.3.3
Suppose
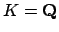
, let

be the archimedean absolute value
and let
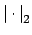
be the

-adic absolute value. Let
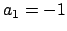
,
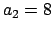
, and

, as in the remark right after
Theorem
16.3.1. Then the theorem implies that there
is an element
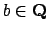
such that
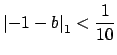
and
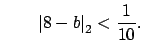
As in the proof of the theorem, we can find such a
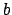
by finding
a
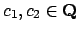
such that
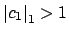
and
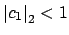
, and
a

and

. For example,
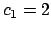
and
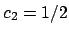
works, since
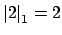
and

and
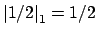
and

. Again
following the proof, we see that for sufficiently large

we can take
We have
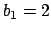
,
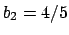
,
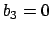
,

,

,

. None of the
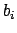
work for
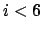
,
but
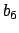
works.

![]() and the
and the
![]() are
are ![]() -adic valuations,
Theorem 16.3.1 is related to the Chinese Remainder
Theorem (Theorem 9.1.3), but the strong approximation theorem
(Theorem 20.4.4) is the
real generalization.
-adic valuations,
Theorem 16.3.1 is related to the Chinese Remainder
Theorem (Theorem 9.1.3), but the strong approximation theorem
(Theorem 20.4.4) is the
real generalization.
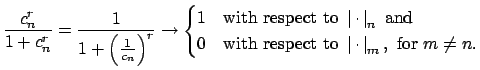
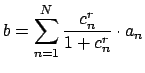
![]() with
with
![]() . Since
. Since
![]() and
and
![]() are
inequivalent (and all absolute values are assumed nontrivial)
there is an
are
inequivalent (and all absolute values are assumed nontrivial)
there is an ![]() such that
such that
![]() . By the case
. By the case ![]() , there is an
, there is an ![]() such
that
such
that
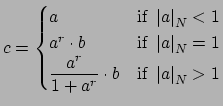
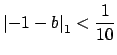 and
and