An amusing observation, which people often argued about
on USENET news back
in the 1990s, is that Fermat's last theorem
is false in
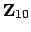 . For example,
. For example,
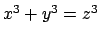 has a nontrivial solution, namely
has a nontrivial solution, namely
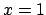 ,
, 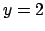 , and
, and
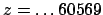 . Here
. Here 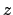 is a cube
root of
is a cube
root of 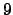 in
in
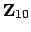 . Note that it takes some work to prove that there
is a cube root of
. Note that it takes some work to prove that there
is a cube root of 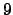 in
in
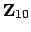 (see Exercise 56).
(see Exercise 56).
William Stein
2004-05-06